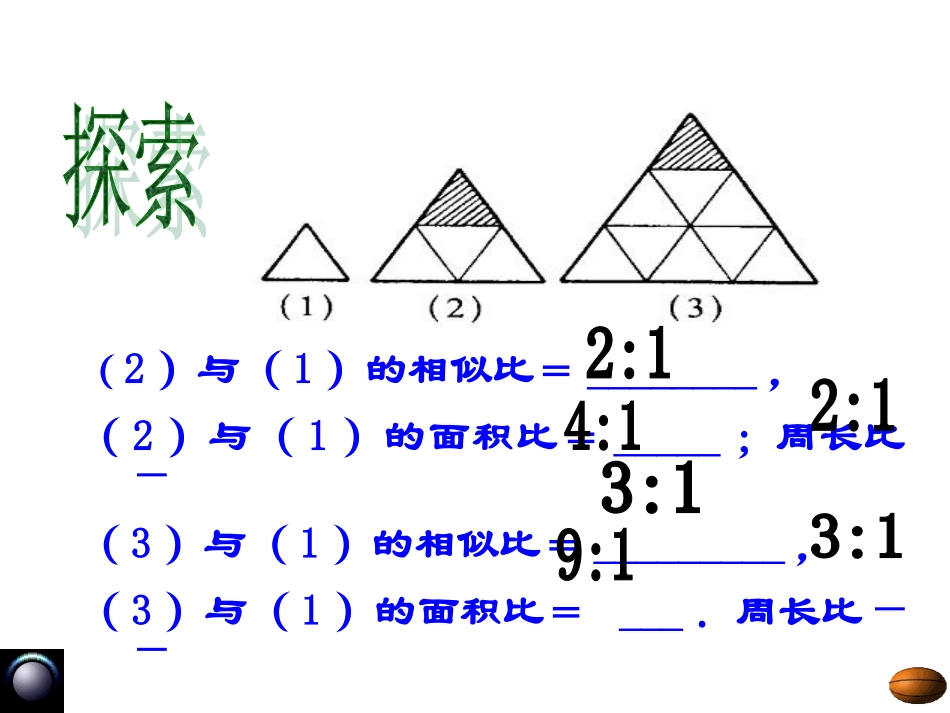
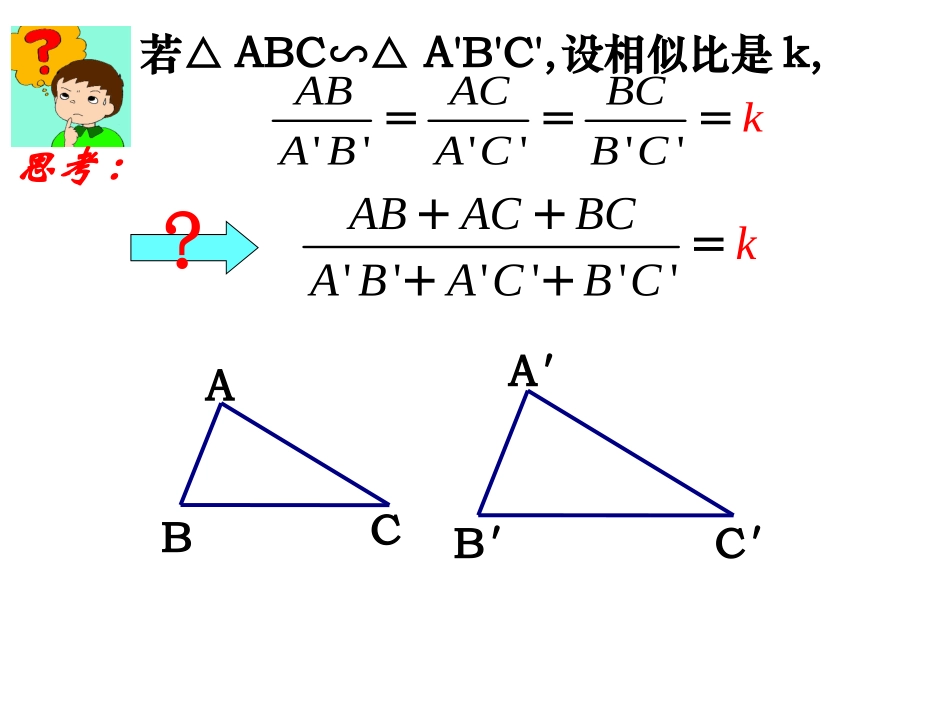
1(2)与(1)的相似比=________,(2)与(1)的面积比=_____;周长比—(3)与(1)的相似比=_________,(3)与(1)的面积比=___.周长比——ABCC′A′B′若△ABC∽△A'B'C',''''''ABACBCABACBkC===''''''ABACBCABACCkB++=++?设相似比是k,思考:''''''''''''kABkACkBCABACBC++++''''''ABACBCABACBC++++''''''ABACBCABACBkC===因为所以''ABkAB=''ACkAC=''BCkBC==所以=k''''''ABACBCABACBkC===''''''ABACBCABACCkB++=++?如图△ABC∽△A'B'C'ABCC′A′B′相似三角形的周长的比等于相似比设相似比是k,类似地:相似多边形的周长的比等于.相似比结论:相似三角形的周长的比等于相似比C'B'A'E'D'DEABC若五边形ABCDE相似于五边形A'B'C'D'E'试说明他们的周长比等于相似比.1.已知△ABC∽△A'B'C'其相似比是2,△ABC的周长是36,则A'B'C'的周长是________.182.小明把1米长的铜丝截成两段,用它们围成两个相似三角形且相似比为3:5,那么截成的两段铜丝的长度差是__________.0.25米类似地:相似多边形的周长的比等于相似比.结论:相似三角形的周长的比等于相似比如果△ABC∽△A'B'C'那么△ABC与△A'B'C'的面积的比与相似比又有什么关系呢?思考:ABCC′A′B′那么?''ADAD=D′C′DABCA′B′△ABC∽△A'B'C'设相似比为k,''BCkBC=则:121''''2BCADBCAD×=×k=┓┓2k=那么''ADADk=CBAABCSSDAADCBBCk相似三角形的面积的比等于相似比的平方.类似地:相似多边形的面积的比等于相似比的平方结论:相似三角形的面积的比等于相似比的平方.类似地:相似多边形的面积的比等于相似比的平方.结论:给形状相同且对应边的比为1:2的两块标牌的表面涂漆,若漆小标牌用漆半听,那么大标牌用漆需要____听.2相似三角形的面积的比等于相似比的平方.类似地:相似多边形的面积的比等于相似比的平方.如图:在△ABC中,M、N分别是AB、AC的中点,(1)△AMN与△ABC的面积比是____;1:4结论:ABCNM(2)△AMN与四边形MNCB的面积比是_________;1:3例题分例题分析析1.在比例尺为1:500的地图上,测得一个三角形地块ABC的周长为12cm,面积为6cm2,求这个地块的实际周长和面积.解:设实际三角形地块△A'B'C'∵△ABC∽△A'B'C',且相似比1500k=∴'''1,500ABCABCCC=2'''1().500ABCABCSS=△A'B'C'的周长=12×500=6000(cm)=60(m)△A'B'C'的面积=6×5002=1500000(cm2)=150(m2)答:这个三角形地块的实际周长为60m,面积为150m2.CBA3、如图,在正方形网格上有△A1B1C1和△ABC,这两个三角形相似吗?如果相似,求出△A1B1C1和△ABC的面积比。ACBA1B1C1例3:如图所示,正方形ABCD中,AB=2,E是BC的中点,DF⊥AE于F.(1)试说明△ABE∽△DFA;(2)求△DFA的面积S1和四边形CDFE的面积S2.FDCBAE如图,把△ABC沿BC边平移到△FED的位置,它们重叠部分的面积是△ABC的面解:∵PE∥AB∴△PEC∽△ABC∴21()9PECABCSECSBC==∴13ECBC=∵BC=3∴EC=1∴CD=ED-EC=BC-EC=2拓展与延伸拓展与延伸GFDABCECD的长.积的,若BC=3,此三角形移动的距离192.四边形ABCD是平行四边形,点E是BC的延长线上的一点,而CE:BC=1:3,试求:(1)△ADG和△EBG的周长比和面积比.(2)若△DFG的面积为9,求△ABG的面积.DFGECBAK3K3K3K4K例题分例题分析析DGEBADFGBA2.如图,DE∥BC,AD:DB=1:2,DC,BE交于点O,则△DOE与△BOC的周长之比是_________,面积比是________.1.两个相似五边形的面积比为9:16,其中较大的五边形的周长为64cm,则较小的五边形的周长为_______cm.ODABCE481:31:9K2k3.如图,已知DE∥FG∥MN∥BC,且AD=DF=FM=MB,求S1:S2:S3:S4DS4S3S2S1ABCEFGMN我有哪些收获呢?我有哪些收获呢?与大家共分享!与大家共分享!学而不思则罔回头一看,我想说…