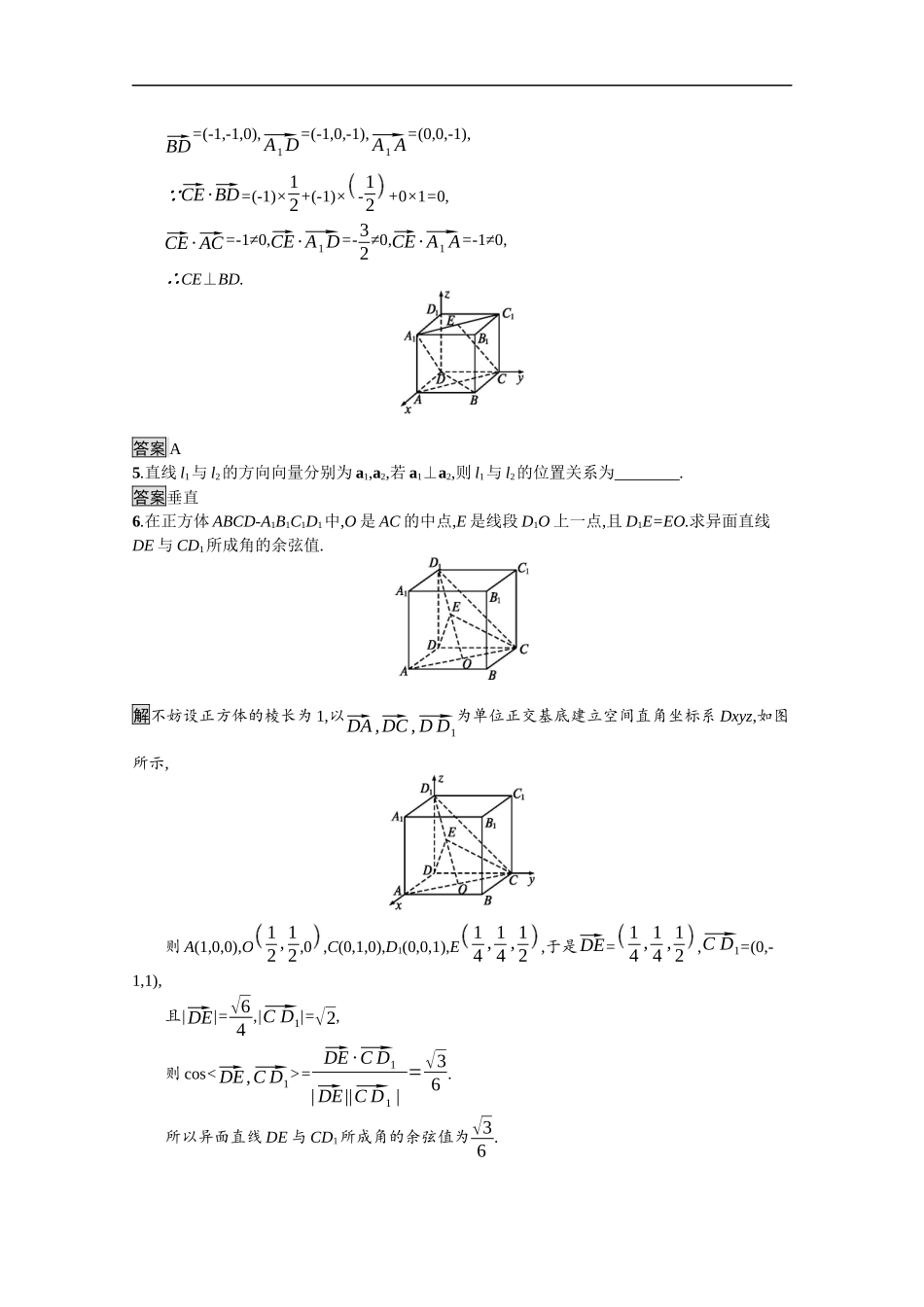
1.2空间向量在立体几何中的应用1.2.1空间中的点、直线与空间向量课后篇巩固提升基础达标练1.已知l1的方向向量为v1=(1,2,3),l2的方向向量为v2=(λ,4,6),若l1∥l2,则λ等于()A.1B.2C.3D.4解析由l1∥l2,得v1∥v2,得1λ=24=36,故λ=2.答案B2.若a=(1,λ,2),b=(2,-1,2),且a与b夹角的余弦值为89,则λ=()A.2B.-2C.-2或255D.2或-255解析a·b=2-λ+4=6-λ,|a|=√5+λ2,|b|=3.cos
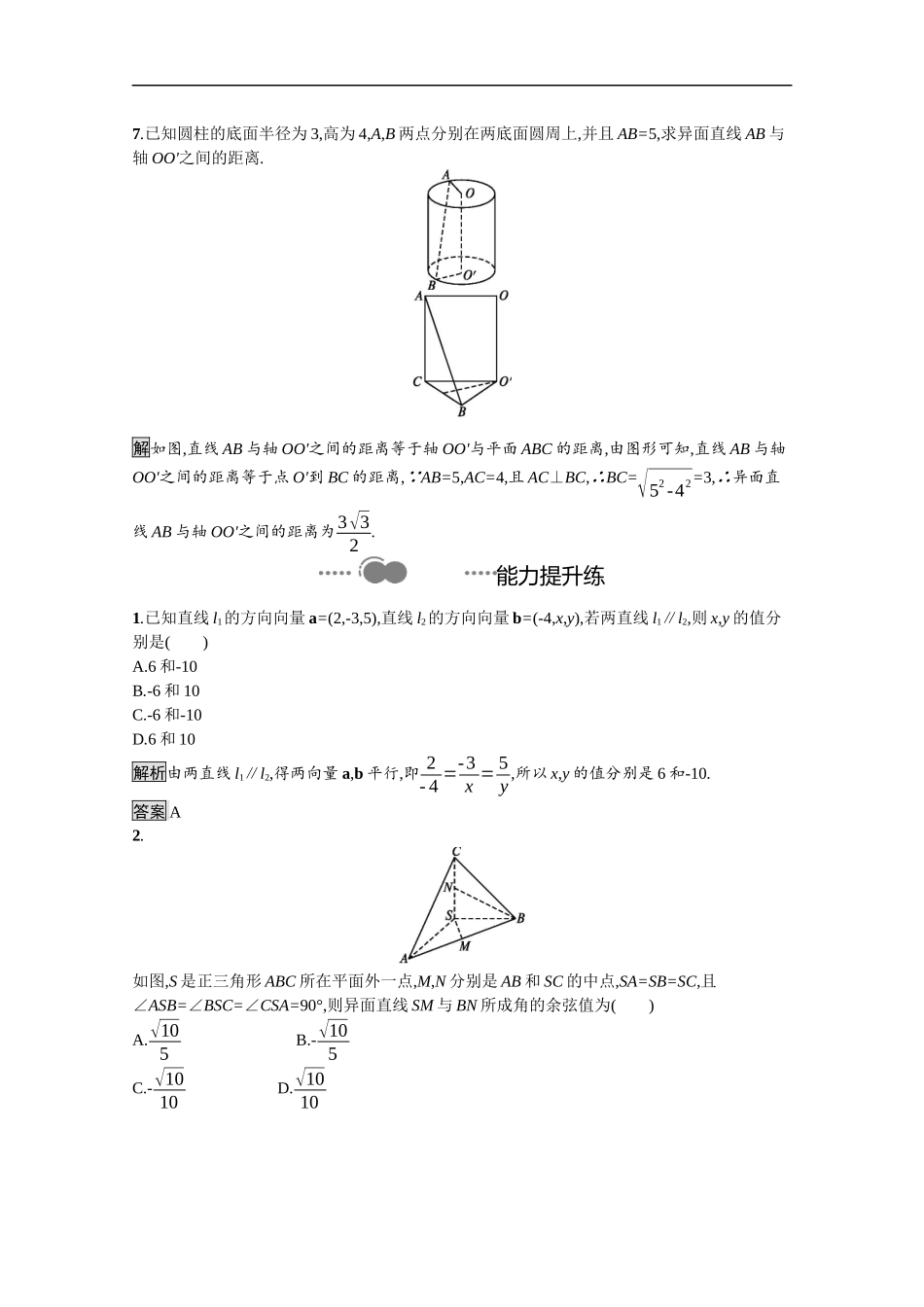
=a·b|a||b|=6-λ√5+λ2·3=89.55λ2+108λ-4=0,解得λ=-2或λ=255.答案C3.若异面直线l1,l2的方向向量分别是a=(0,-2,-1),b=(2,0,4),则异面直线l1与l2的夹角的余弦值等于()A.-25B.25C.-2√55D.2√55解析a·b=-4,|a|=√5,|b|=2√5,cosθ=|cos|=|a·b|a||b||=|-410|=25.答案B4.在正方体ABCD-A1B1C1D1中,若E为A1C1的中点,则直线CE垂直于()A.BDB.ACC.A1DD.A1A解析以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系Dxyz.设正方体的棱长为1.则C(0,1,0),B(1,1,0),A(1,0,0),D(0,0,0),C1(0,1,1),A1(1,0,1),E12,12,1,∴⃗CE=12,-12,1,⃗AC=(-1,1,0),⃗BD=(-1,-1,0),⃗A1D=(-1,0,-1),⃗A1A=(0,0,-1), ⃗CE·⃗BD=(-1)×12+(-1)×-12+0×1=0,⃗CE·⃗AC=-1≠0,⃗CE·⃗A1D=-32≠0,⃗CE·⃗A1A=-1≠0,∴CE⊥BD.答案A5.直线l1与l2的方向向量分别为a1,a2,若a1⊥a2,则l1与l2的位置关系为.答案垂直6.在正方体ABCD-A1B1C1D1中,O是AC的中点,E是线段D1O上一点,且D1E=EO.求异面直线DE与CD1所成角的余弦值.解不妨设正方体的棱长为1,以⃗DA,⃗DC,⃗DD1为单位正交基底建立空间直角坐标系Dxyz,如图所示,则A(1,0,0),O12,12,0,C(0,1,0),D1(0,0,1),E14,14,12,于是⃗DE=14,14,12,⃗CD1=(0,-1,1),且|⃗DE|=√64,|⃗CD1|=√2,则cos<⃗DE,⃗CD1>=⃗DE·⃗CD1|⃗DE||⃗CD1|=√36.所以异面直线DE与CD1所成角的余弦值为√36.7.已知圆柱的底面半径为3,高为4,A,B两点分别在两底面圆周上,并且AB=5,求异面直线AB与轴OO'之间的距离.解如图,直线AB与轴OO'之间的距离等于轴OO'与平面ABC的距离,由图形可知,直线AB与轴OO'之间的距离等于点O'到BC的距离, AB=5,AC=4,且AC⊥BC,∴BC=√52-42=3,∴异面直线AB与轴OO'之间的距离为3√32.能力提升练1.已知直线l1的方向向量a=(2,-3,5),直线l2的方向向量b=(-4,x,y),若两直线l1∥l2,则x,y的值分别是()A.6和-10B.-6和10C.-6和-10D.6和10解析由两直线l1∥l2,得两向量a,b平行,即2-4=-3x=5y,所以x,y的值分别是6和-10.答案A2.如图,S是正三角形ABC所在平面外一点,M,N分别是AB和SC的中点,SA=SB=SC,且∠ASB=∠BSC=∠CSA=90°,则异面直线SM与BN所成角的余弦值为()A.√105B.-√105C.-√1010D.√1010解析不妨设SA=SB=SC=1,以S为坐标原点,⃗SA,⃗SB,⃗SC所在直线分别为x轴,y轴,z轴,建立空间直角坐标系Sxyz,则相关各点坐标为B(0,1,0),S(0,0,0),M12,12,0,N0,0,12.因为⃗SM=12,12,0,⃗BN=0,-1,12,所以|⃗SM|=√22,|⃗BN|=√52,⃗SM·⃗BN=-12,cos<⃗SM,⃗BN>=⃗SM·⃗BN|⃗SM||⃗BN|=-√105,因为异面直线所成的角为锐角或直角,所以异面直线SM与BN所成角的余弦值为√105.答案A3.如图,在三棱锥S-ABC中,SA⊥平面ABC,AB⊥BC,且SA=AB=BC=1,则异面直线SB与AC之间的距离为.解析构造如图所示正方体.取AB的中点O,连接OD交AC于点E,连接OM交SB于点F,由平面几何知识可知,OF=13OM,OE=13OD,所以EF∥13DM.又因为AC⊥BD,AC⊥BM,所以AC⊥平面BDM,AC⊥DM,因为EF∥13DM,所以AC⊥EF.同理可证SB⊥DM,所以SB⊥EF.所以EF是异面直线AC和SB的公垂线段.所以EF=13DM=√33.答案√334.如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中,①GH与EF平行;②BD与MN为异面直线;③GH与MN成60°角;④DE与MN垂直.以上四个命题中,正确命题的序号是.解析还原成正四面体知GH与EF为异面直线,BD与MN为异面直线,GH与MN成60°角,DE与MN为异面垂直.答案②③④5.如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1,设P为AC的中点,Q在AB上且AB=3AQ,证明:PQ⊥OA.证明如图,连接OP,OQ,PQ,取O为坐标原点,过点O作OD⊥OA,以OA,OD,OC所在直线为x轴,y轴,z轴,建立空间直角坐标系Oxyz(如图所示).则A(1,0,0),C(0,0,1),B-12,√32,...