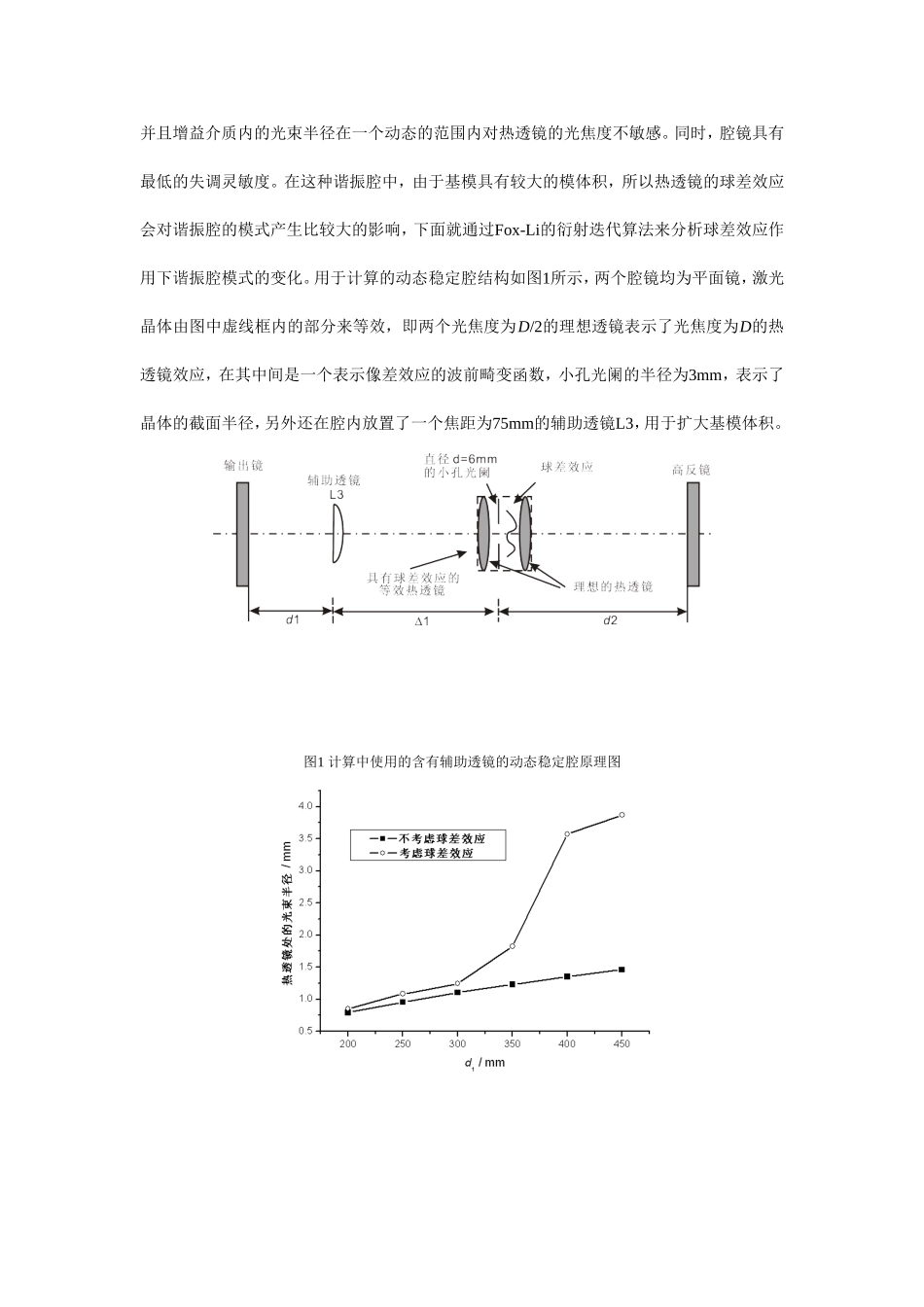
热透镜的球差效应对大基模体积激光的影响学号:10706121引言我们知道,热透镜的球差效应在采用闪光灯漫反射抽运方式的固体激光器中不能忽略,而且对于激光二极管抽运的情况也具有重要的意义,因为随着半导体工艺的发展,大功率激光二极管被越来越多的用作固体激光器的抽运源,总的抽运功率可以达到千瓦量级,激光二极管侧向抽运更易于在晶体内部形成温度分布不均匀,从而加剧了热透镜的球差效应。所以在强抽运的条件下,激光晶体热透镜的球差效应是不容忽视的,尤其是在大基模体积的动态稳定腔中,会影响谐振腔的振荡模式,进而影响腔内损耗和输出功率。1.镜球差效应的原理所谓的热透镜球差效应是指,由于激光器抽运不均匀带来的增益介质温度沿径向分布不均匀,从而使得晶体的热传导系数K和热光系数dn/dT也沿径向分布不均匀,最终导致热透镜的光焦度D也成为径向坐标r的函数D(r),这样,热透镜就成为一个具有像差(球差)的透镜。下面给出表征热透镜球差效应的公式。对于大部分激光器的而言,抽运方式的设计使得在介质截面上的增益分布不可能是均匀的,从而使介质中吸收热量的分布也存在不均匀性。设增益介质截面半径为r0,长度为L,其单位体积内吸收的热量Q沿径向的分布函数为,(1)其中Ph为介质中总的热沉积量,参数为抽运不均匀度。再考虑到热传导系数K和热光系数dn/dT随温度T的变化,分别如下式所示,,(2),(3)其中K0是T=300K时介质的热传导系数,通过求解热传导方程,最终得到晶体内部温度T和折射率n沿径向的变化关系为[7],,(4),(5)其中Tc是介质中心处的温度,A、B是与抽运和温度的不均匀度有关的参数[7],和是与热光效应和应力双折射效应有关的参数[7]。观察公式(4)和公式(5)发现,温度和折射率的分布中都出现了四次项,而不再是理想的抛物线式分布。在表达折射率分布的公式(5)中,二次项的系数表示了热透镜效应的强弱,四次项的系数则表示了球差效应的强弱。准确的表达热透镜球差效应的强弱,可以通过一束无像差的平面波经过热透镜以后,具有球差效应的波前与理想球面波波前的光程差(opticalpathdifference,OPD)来表示,对于内部折射率分布函数如公式(5)所示的激光晶体,其热透镜的球差效应可以表示,(6)其中是与激光晶体内光束分布有关的因子。可见,球差效应的强弱主要是由折射率分布函数公式(5)中的四次项系数所决定的,另外还与晶体的长度L及因子有关。2.球差效应对基模动态稳定腔模式的影响传统的激光谐振腔由于受到热透镜效应的影响,基模的模体积很小,为了获得基模输出,需要在腔内加入小孔光阑,从而限制了基模输出功率的提高。为了获得大功率的基模输出,Magni等人提出了动态稳定腔的概念,这种谐振腔具有以下特点:基模具有比较大的模体积,并且增益介质内的光束半径在一个动态的范围内对热透镜的光焦度不敏感。同时,腔镜具有最低的失调灵敏度。在这种谐振腔中,由于基模具有较大的模体积,所以热透镜的球差效应会对谐振腔的模式产生比较大的影响,下面就通过Fox-Li的衍射迭代算法来分析球差效应作用下谐振腔模式的变化。用于计算的动态稳定腔结构如图1所示,两个腔镜均为平面镜,激光晶体由图中虚线框内的部分来等效,即两个光焦度为D/2的理想透镜表示了光焦度为D的热透镜效应,在其中间是一个表示像差效应的波前畸变函数,小孔光阑的半径为3mm,表示了晶体的截面半径,另外还在腔内放置了一个焦距为75mm的辅助透镜L3,用于扩大基模体积。图1计算中使用的含有辅助透镜的动态稳定腔原理图图2热透镜处的光束半径随d1的变化关系通过对上述谐振腔的研究发现,在参数和d2固定不变的情况下,通过改变d1的值可以改变热透镜处的光束半径大小,图2给出了=302.5mm和d2=370mm的情况下,不考虑球差效应时高斯光束在热透镜处的光束半径随d1的变化关系,计算中热透镜焦距的选择总是保证激光器的工作点在稳定区的中间,即满足动态稳定的条件。从图中可以看出,在d1从200mm变化到450mm的过程中,光束半径从0.79mm变化为1.46mm。d1的值分别为250mm,350mm和450mm时,高斯光束在热透镜处的光...