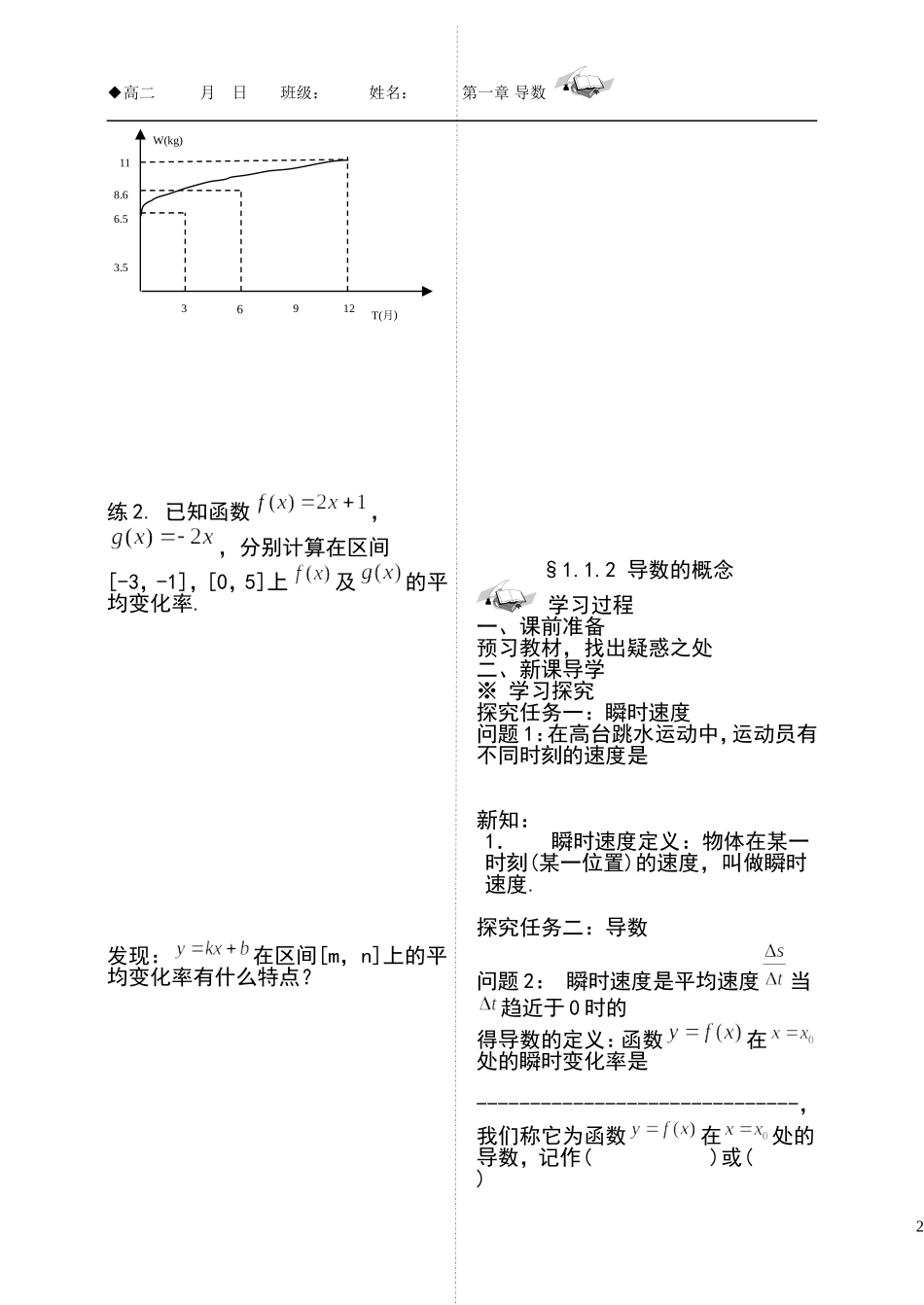
◆高二月日班级:姓名:第一章导数§1.1.1变化率问题学习过程新课导学※学习探究探究任务一:问题1:气球膨胀率,求平均膨胀率吹气球时,随着气球内空气容量的增加,气球的半径增加得越来越慢从数学的角度如何描述这种现象?问题2:高台跳水,求平均速度新知:平均变化率:试试:设,是数轴上的一个定点,在数轴上另取一点,与的差记为,即=或者=,就表示从到的变化量或增量相应地,函数的变化量或增量记为即=;如果它们的比值,则上式就表示为,此比值就称为平均变化率.反思:所谓平均变化率也就是的增量与的增量的比值.※典型例题例1过曲线上两点和作曲线的割线,求出当时割线的斜率.例2已知函数,分别计算在下列区间上的平均变化率:(1)[1,3];(2)[1,2];(3)[1,1.1];小结:※动手试试练1.某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率.1◆高二月日班级:姓名:第一章导数练2.已知函数,,分别计算在区间[-3,-1],[0,5]上及的平均变化率.发现:在区间[m,n]上的平均变化率有什么特点?§1.1.2导数的概念学习过程一、课前准备预习教材,找出疑惑之处二、新课导学※学习探究探究任务一:瞬时速度问题1:在高台跳水运动中,运动员有不同时刻的速度是新知:1.瞬时速度定义:物体在某一时刻(某一位置)的速度,叫做瞬时速度.探究任务二:导数问题2:瞬时速度是平均速度当趋近于0时的得导数的定义:函数在处的瞬时变化率是------------------------------,我们称它为函数在处的导数,记作()或()T(月)W(kg)639123.56.58.6112◆高二月日班级:姓名:第一章导数即注意:(1)函数应在点的附近有定义,否则导数不存在奎屯王新敞新疆(2)在定义导数的极限式中,趋近于0可正、可负、但不为0,而可以为0奎屯王新敞新疆(3)是函数对自变量在范围内的平均变化率,它的几何意义是(4)导数是函数在点的处瞬时变化率,它反映的函数在点处变化()程度.小结:由导数定义,高度h关于时间t的导数就是运动员的瞬时速度,气球半径关于体积V的导数就是气球的瞬时膨胀率.※典型例题例1将原油精炼为汽油、柴油、塑胶等各种不同产品,需要对原油进行冷却和加热.如果在第xh时,原油的温度(单位:)为.计算第3h和第5h时,原油温度的瞬时变化率,并说明它们的意义.总结:函数平均变化率的符号刻画的是();它的绝对值反映().例2已知质点M按规律s=2t2+3做直线运动(位移单位:cm,时间单位:s),(1)当t=2,Δt=0.01时,求.(2)当t=2,Δt=0.001时,求.(3)求质点M在t=2时的瞬时速度小结:利用导数的定义求导,步骤为:第一步,第二步:第三步:3◆高二月日班级:姓名:第一章导数※动手试试练1一球沿一斜面自由滚下,其运动方程是(位移单位:m,时间单位:s),求小球在时的瞬时速度奎屯王新敞新疆§1.1.3导数的几何意义学习目标通过导数的图形变换理解导数的几何意义就是曲线在该点的切线的斜率,理解导数的概念并会运用概念求导数.学习过程一、课前准备(预习教材,找出疑惑之处)复习1:曲线上向上的连线称为曲线的割线,斜率复习2:设函数在附近有定义当自变量在附近改变时,函数值也相应地改变,如果当时,平均变化率趋近于一个常数,则数称为函数在点的瞬时变化率.记作:当时,二、新课导学※学习探究探究任务:导数的几何意义问题1:当点,沿着曲线趋近于点时,割线的变化趋是什么?新知:当割线P无限地趋近于某一极限位置PT奎屯王新敞新疆我们就把极限位置上的直线PT,叫做曲线C在点P处的切线奎屯王新敞新疆割线的斜率是:\当点无限趋近于点P时,无限4◆高二月日班级:姓名:第一章导数趋近于切线PT的斜率.因此,函数在处的导数就是切线PT的斜率,即()新知:函数在处的导数的几何意义是曲线在处切线的斜率.即=※典型例题例1如图,它表示跳水运动中高度随时间变化的函数的图象.根据图象,请描述、比较曲线在附近的变化情况.小结:例2如图,它表示人体血管中药物浓度(单位:)随时间(单位:min)变化的函数图象.根据图象,估计=0.2,0.4,0.6,0.8时,血管中药物浓度的瞬时变化率(精确到0.1)※动手试试练1.求双曲线在点处的切线的斜率,并写出切线方...