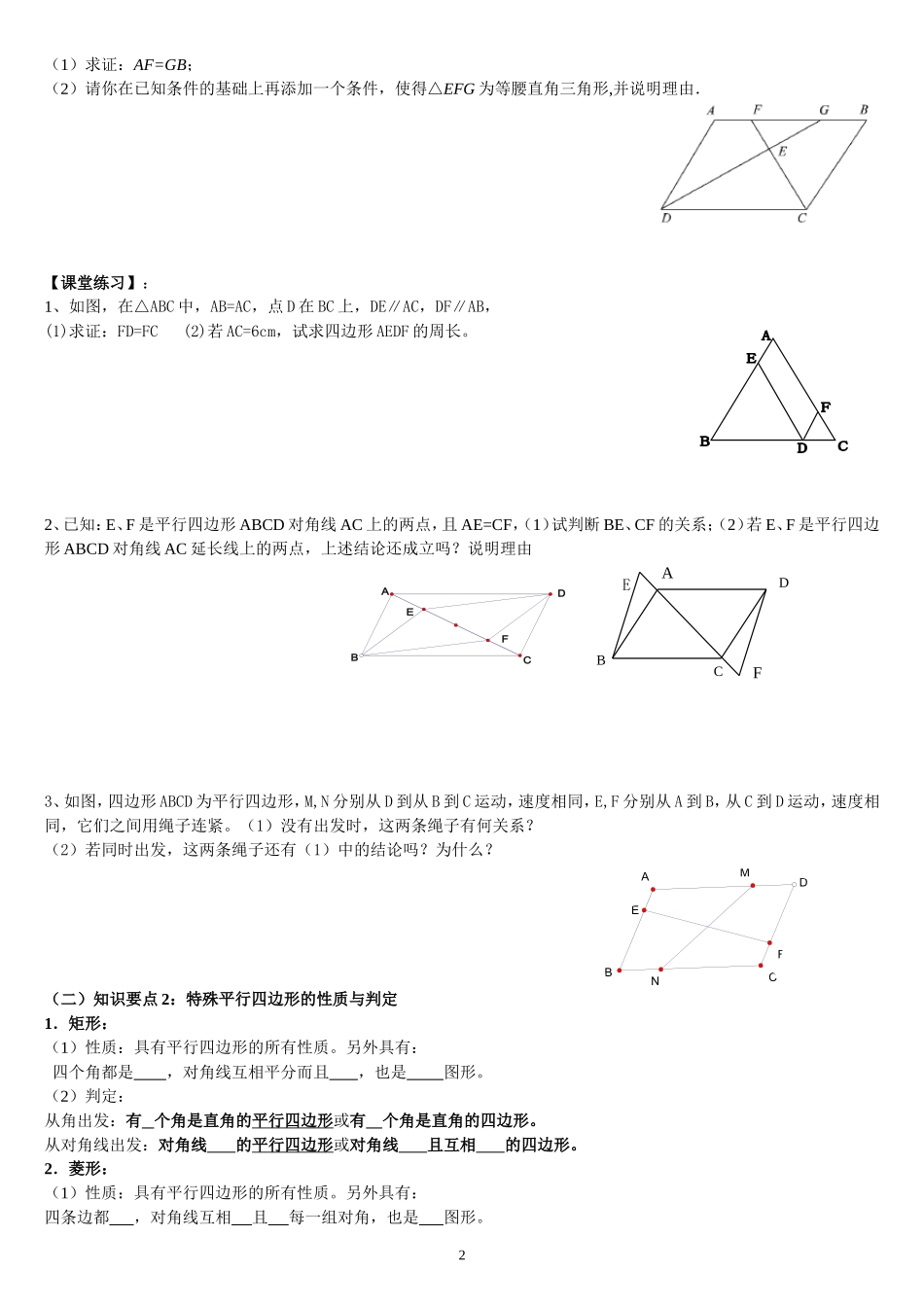
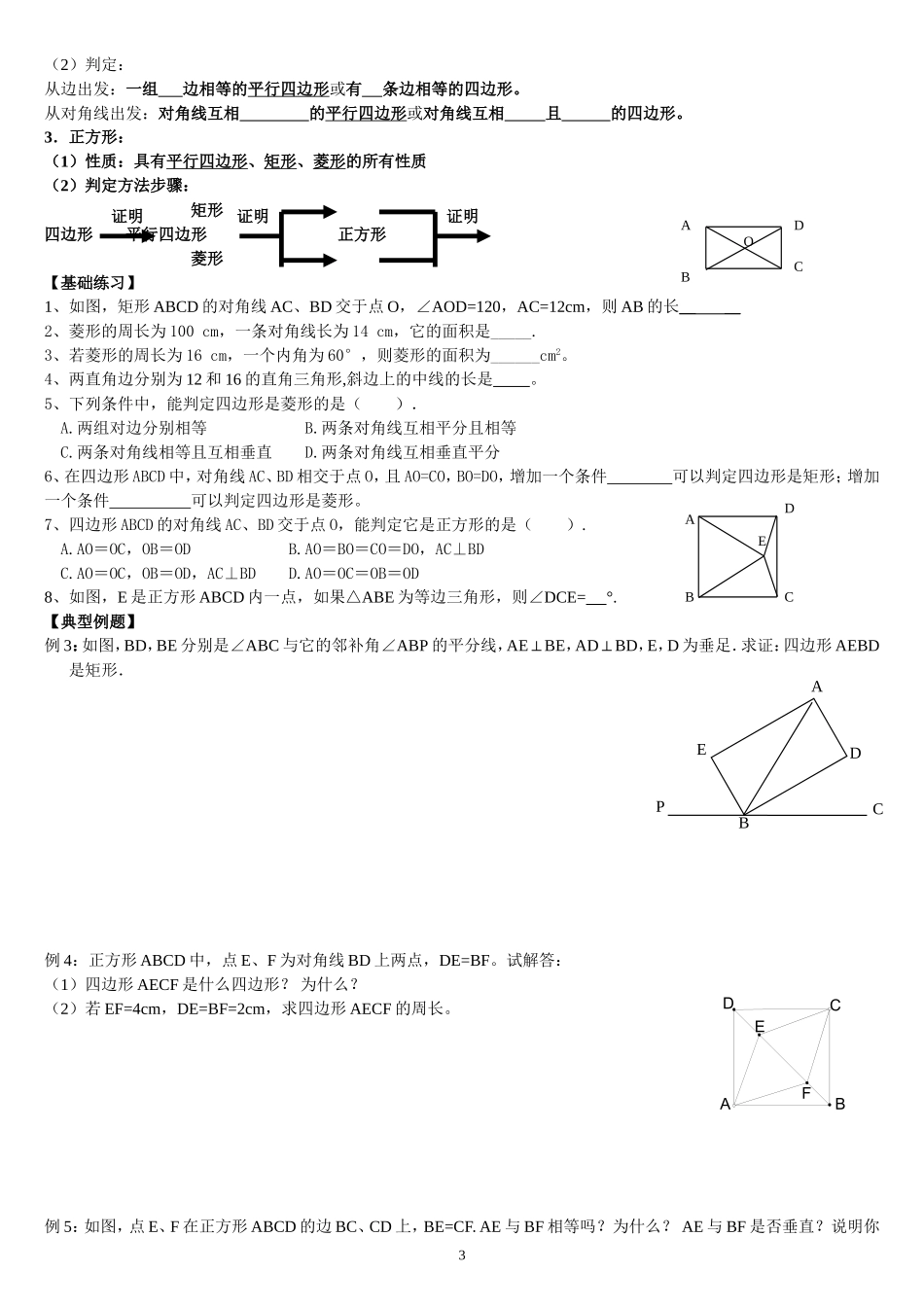
八年级下册复习---平行四边形一、学习目标复习平行四边形、特殊平行四边形、梯形的性质与判定,能利用它们进行计算或证明.二、学习重难点重点:性质与判定的运用;难点:证明过程的书写。三、本章知识结构图1.平行四边形是特殊的;特殊的平行四边形包括、、。2.梯形(是否)特殊平行四边形,(是否)特殊四边形。3.特殊的梯形包括梯形和梯形。4、本章学过的四边形中,属于轴对称图形的有;属于中心对称图形的有。四、复习过程(一)知识要点1:平行四边形的性质与判定1.平行四边形的性质:(1)从边看:对边,对边;(2)从角看:对角,邻角;(3)从对角线看:对角线互相;(4)从对称性看:平行四边形是图形。2、平行四边形的判定:(1)判定1:两组对边分别的四边形是平行四边形。(定义)(2)判定2:两组对边分别的四边形是平行四边形。(3)判定3:一组对边且的四边形是平行四边形。(4)判定4:两组对角分别的四边形是平行四边形。(5)判定5:对角线互相的四边形是平行四边形。【基础练习】1.已知□ABCD中,∠B=70°,则∠A=____,∠C=____,∠D=____.2.已知O是ABCD的对角线的交点,AC=38mm,BD=24mm,AD=14mm,那么△BOC的周长等于____.3.如图1,ABCD中,对角线AC和BD交于点O,若AC=8,BD=6,则边AB长的取值范围是().A.1<AB<7B.2<AB<14C.6<AB<8D.3<AB<44.不能判定四边形ABCD为平行四边形的题设是()A.AB=CD,AD=BCB.ABCDC.AB=CD,AD∥BCD.AB∥CD,AD∥BC5.在ABCD中,AE⊥BC于E,AF⊥CD于F,AE=4,AF=6,ABCD的周长为40,则ABCD的面积是()A、36B、48C、40D、24【典型例题】例1、若平行四边形ABCD的周长是20cm,△AOD的周长比△ABO的周长大6cm.求AB,AD的长.例2、如图,已知四边形ABCD是平行四边形,∠BCD的平分线CF交边AB于F,∠ADC的平分线DG交边AB于G。1FEDCBAOABCDOABCDDCABEFMNBEFCAD(1)求证:AF=GB;(2)请你在已知条件的基础上再添加一个条件,使得△EFG为等腰直角三角形,并说明理由.【课堂练习】:1、如图,在△ABC中,AB=AC,点D在BC上,DE∥AC,DF∥AB,(1)求证:FD=FC(2)若AC=6cm,试求四边形AEDF的周长。2、已知:E、F是平行四边形ABCD对角线AC上的两点,且AE=CF,(1)试判断BE、CF的关系;(2)若E、F是平行四边形ABCD对角线AC延长线上的两点,上述结论还成立吗?说明理由3、如图,四边形ABCD为平行四边形,M,N分别从D到从B到C运动,速度相同,E,F分别从A到B,从C到D运动,速度相同,它们之间用绳子连紧。(1)没有出发时,这两条绳子有何关系?(2)若同时出发,这两条绳子还有(1)中的结论吗?为什么?(二)知识要点2:特殊平行四边形的性质与判定1.矩形:(1)性质:具有平行四边形的所有性质。另外具有:四个角都是,对角线互相平分而且,也是图形。(2)判定:从角出发:有个角是直角的平行四边形或有个角是直角的四边形。从对角线出发:对角线的平行四边形或对角线且互相的四边形。2.菱形:(1)性质:具有平行四边形的所有性质。另外具有:四条边都,对角线互相且每一组对角,也是图形。2FEDCBAABCDE(2)判定:从边出发:一组边相等的平行四边形或有条边相等的四边形。从对角线出发:对角线互相的平行四边形或对角线互相且的四边形。3.正方形:(1)性质:具有平行四边形、矩形、菱形的所有性质(2)判定方法步骤:矩形四边形平行四边形正方形菱形【基础练习】1、如图,矩形ABCD的对角线AC、BD交于点O,∠AOD=120,AC=12cm,则AB的长____2、菱形的周长为100cm,一条对角线长为14cm,它的面积是_____.3、若菱形的周长为16cm,一个内角为60°,则菱形的面积为______cm2。4、两直角边分别为12和16的直角三角形,斜边上的中线的长是。5、下列条件中,能判定四边形是菱形的是().A.两组对边分别相等B.两条对角线互相平分且相等C.两条对角线相等且互相垂直D.两条对角线互相垂直平分6、在四边形ABCD中,对角线AC、BD相交于点O,且AO=CO,BO=DO,增加一个条件可以判定四边形是矩形;增加一个条件可以判定四边形是菱形。7、四边形ABCD的对角线AC、BD交于点O,能判定它是正方形的是().A.AO=OC,OB=ODB.AO=BO=CO=DO,AC⊥BDC.AO=OC...