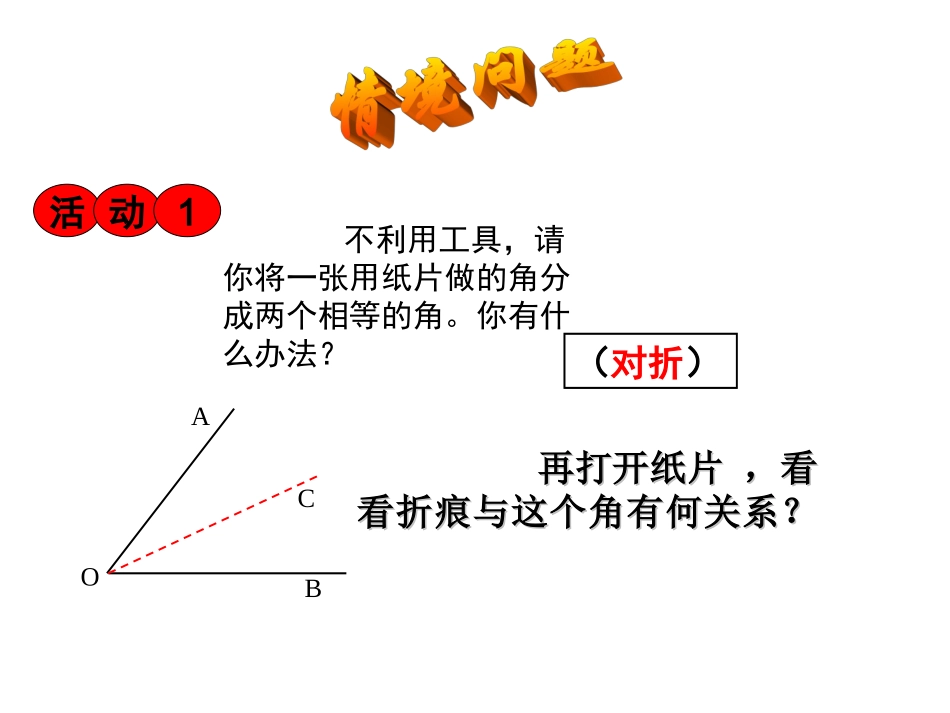
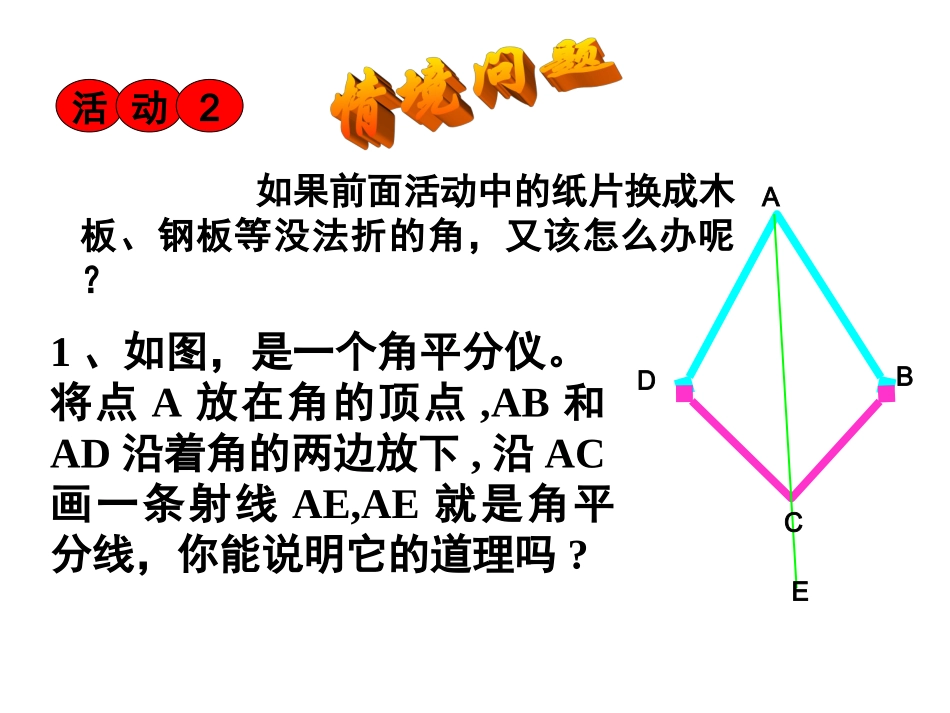
12.3角平分线的性质(一)AOBC活动1再打开纸片,看再打开纸片,看看折痕与这个角有何关系?看折痕与这个角有何关系?(对折)不利用工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?1、如图,是一个角平分仪。将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗?活动2如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?ADCBEADBCE2、证明:在△ACD和△ACB中AD=AB(已知)DC=BC(已知)CA=CA(公共边)∴△ACDACB≌△(SSS)∴∠CAD=CAB∠(全等三角形的对应边相等)∴AC平分∠DAB(角平分线的定义)OABCE活动3NOMCENM根据角平分仪的制作原理怎样作一个角的平分线?(不用角平分仪或量角器)探究角平分线的性质活动4(2)猜想:角的平分线上的点到角的两边的距离相等.(1)实验:将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?PAOBCED12已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E求证:PD=PE探究角平分线的性质(3)验证猜想证明:∵OC平分∠AOB(已知)∴∠1=2∠(角平分线的定义)∵PDOA⊥,PEOB⊥(已知)∴∠PDO=PEO∠(垂直的定义)在△PDO和△PEO中∠PDO=PEO∠(已证)∠1=2∠(已证)OP=OP(公共边)∴△PDOPEO≌△(AAS)∴PD=PE(全等三角形的对应边相等)如图:在△ABC中,∠C=90°AD是∠BAC的平分线,DEAB⊥于E,F在AC上,BD=DF。求证:CF=EBACDEBF试试自己写证明。你一定行!一、过程小结:情境→观察→作图→应用→探究→再应用二、知识小结:本节课学习了那些知识?有哪些运用?你学了吗?做了吗?用了吗?再见