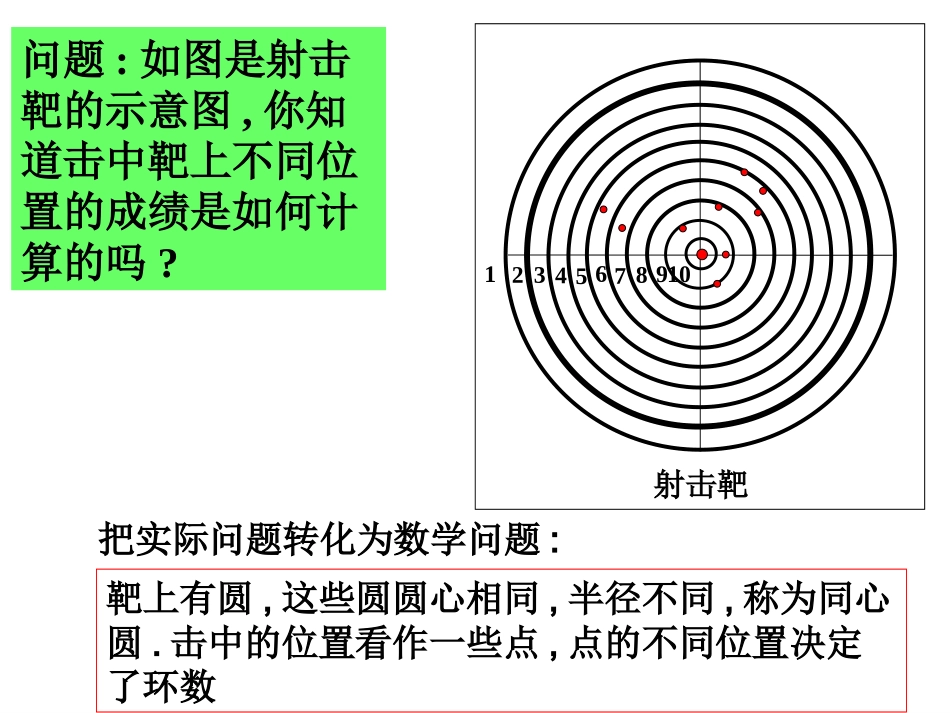
12345678910射击靶问题:如图是射击靶的示意图,你知道击中靶上不同位置的成绩是如何计算的吗?把实际问题转化为数学问题:靶上有圆,这些圆圆心相同,半径不同,称为同心圆.击中的位置看作一些点,点的不同位置决定了环数设⊙O的半径为r,点到圆心的距离为d。则点和圆的位置关系点在圆内dr﹤点在圆上点在圆外d=rd>r练习:已知圆的直径等于10厘米,点到圆心的距离是:A、8厘米B、4厘米C、5厘米。请你分别说出点与圆的位置关系。●●●●Oddd例1、如图,已知直角三角形ABC的边AB=3厘米,AC=4厘米。AD是高,AE是中线(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D、E与圆A的位置关系如何?典型例题(2)若以A点为圆心作圆A,使B、C、DE四点中至少有一个点在圆内,有一个点在圆外则圆A的半径r多少?DCEBA课堂练习(1).P93(1,2)(2).如图所示,两圆的半径都是1cm,则图中重叠部分的面积的点表示()A到圆心P,Q的距离都大于1cm的所有点的集合B到圆心P,Q的距离都等于1cm的所有点的集合C到圆心P,Q的距离都小于1cm的所有点的集合D到圆心P,Q的距离都不大于1cm的所有点的集合..PQD探究①:过一个已知点A可以画多少个圆?A无数个探究②:过已知两点A、B画多少个圆?结论:经过两点的圆的圆心必定在两点连线段的中垂线上。ABABC为什么过同一直线上的三点不能作圆呢?因为DE∥FG,所以没有交点,即没有过这三点的圆心DFEG探究③过三点能作几个圆?1.三点共线(不能作圆)参见课本P99反证法ABC1、连结AB,作线段AB的垂直平分线DE,ODEGF2、连结BC,作线段BC的垂直平分线FG,交DE于点O,3、以O为圆心,OB为半径作圆,作法:⊙O就是所求作的圆已知:不在同一直线上的三点A、B、C求作:⊙O,使它经过A、B、C2、三点不共线定理:定理:不在同一直线上的三点确定一个圆O由定理可知:经过三角形三个顶点可以作一个圆,经过三角形各顶点的圆叫做三角形的外接圆。外接圆的圆心叫做三角形的外心,这个三角形叫做这个圆的内接三角形。ABC圆的内接三角形三角形的外接圆三角形的外心ABCO外心1。三边垂直平分线的交点2。到三个顶点距离相等OABCABCO直角三角形外心是斜边AB的中点钝角三角形外心在△ABC的外面三角形的外心是否一定在三角形的内部?三角形与圆的位置关系•分别作出锐角三角形,直角三角形,钝角三角形的外接圆,并说明与它们外心的位置情况锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角形斜边中点,钝角三角形的外心位于三角形外.老师期望:作三角形的外接圆是必备基本技能,定要熟练掌握.ABC●OABCCAB┐●O●O分工合作观察发现思考:任意四个点是不是可以作一个圆?请举例说明.不一定1.四点在一条直线上不能作圆;3.四点中任意三点不在一条直线可能作圆也可能作不出一个圆.ABCDABCDABCDABCD2.三点在同一直线上,另一点不在这条直线上不能作圆;课堂练习1、判断题:1)过三点一定可以作圆()2)三角形有且只有一个外接圆()3)任意一个圆有一个内接三角形,并且只有一个内接三角形()4)三角形的外心就是这个三角形任意两边垂直平分线的交点()5)三角形的外心到三边的距离相等()错对错对错2.如图,已知RtABC⊿中,若AC=12cm,BC=5cm,外接圆半径=cm。90CCBA3.如图,已知等边三角形ABC中,边长为6cm,求它的外接圆半径。OEDCBA4.如图,等腰⊿ABC中,,,求外接圆的半径。13ABACcm10BCcmOADCB古时候有个人叫王戎,7岁那年的某一天和小伙伴在路边玩,看见一棵李子树上的果实多得把树枝都快压断了,小伙伴们都跑去摘,只有王戎站着没动。他说:“李子是苦的,我不吃。”小伙伴摘来一尝,李子果然苦的没法吃。路边苦李路边苦李小故事小伙伴问王戎:“这就怪了!你又没有吃,怎么知道李子是苦的啊?”王戎说:“如果李子是甜的,树长在路边,李子早就没了!李子现在还那么多,所以啊,肯定李子是苦的,不好吃!”小华睡觉前,地上是干的,早晨起来,看见地上全湿了。小华对婷婷说:“昨天晚上下雨了。”你能对小华的判断说出理由吗?假设昨天晚上没有下雨,那么地上应是干的,这与早晨地上全湿了相矛盾,所以说昨晚下雨是正确的。小华的理由:我们可以把这种说理方法应用到数学问题上。先假设结论...