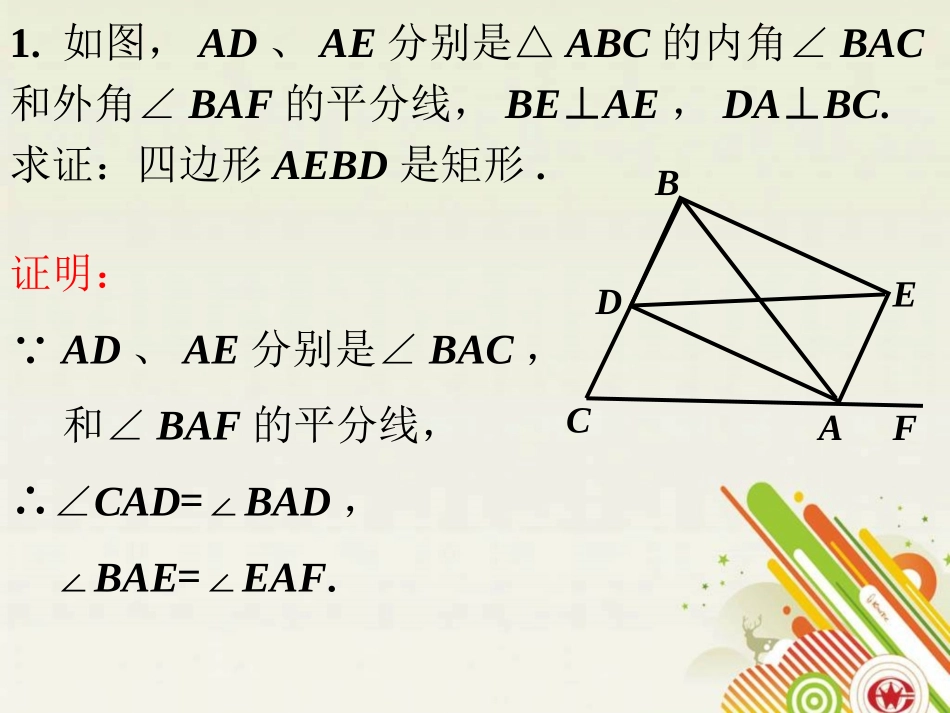
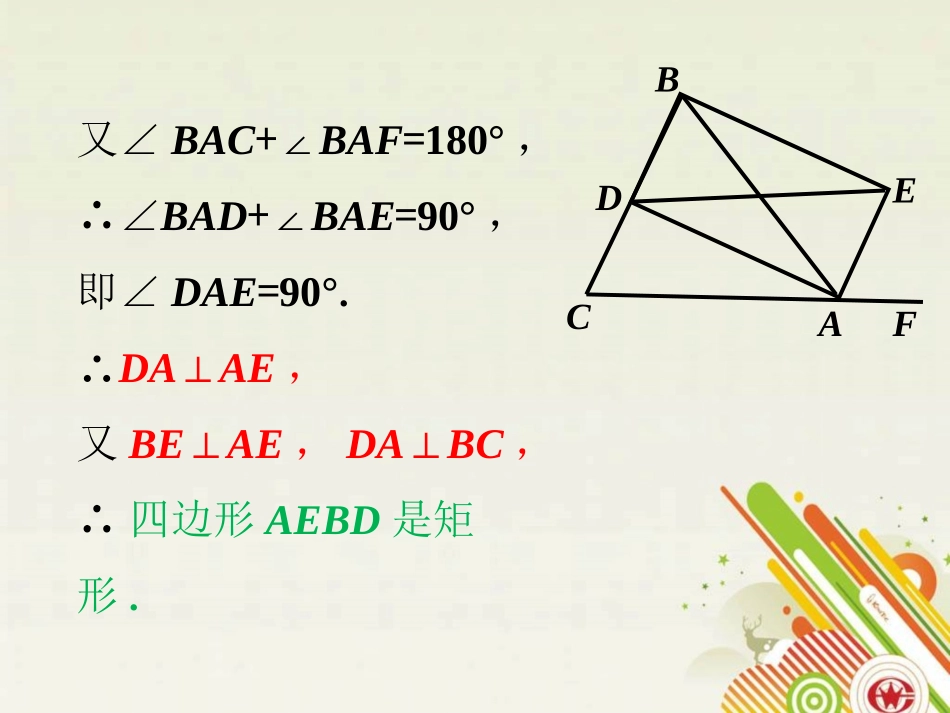
1.如图,AD、AE分别是△ABC的内角∠BAC和外角∠BAF的平分线,BE⊥AE,DA⊥BC.求证:四边形AEBD是矩形.CAFBED证明:∵AD、AE分别是∠BAC,和∠BAF的平分线,∴∠CAD=∠BAD,∠BAE=∠EAF.又∠BAC+∠BAF=180°,∴∠BAD+∠BAE=90°,即∠DAE=90°.∴DA⊥AE,又BE⊥AE,DA⊥BC,∴四边形AEBD是矩形.CAFBED2.一个四边形满足:它的每个顶点到其他三个顶点的距离之和相等.试证明该四边形为矩形.解:以A点的角度看,S=AB+AD+AC……①.以B点的角度看,S=BA+BD+BC……②.以C点的角度看,S=CA+CB+CD……③.以D点的角度看,S=DA+DB+DC……④.DABC由②、④得AD+DC=AB+BC……(1),由①、③得BA+AD=CB+CD……(2),由(1)+(2)得2AD=2BC,∴AD=BC把这个结论代入(1)得DC=AB,∴四边形是平行四边形.又对角线相等,∴四边形是矩形.3.如图,将ABCD的边DC延长到点E,使CE=DC,连结AE,交BC于点F,∠AFC=2∠D,连结AC、BE.求证:四边形ABEC是矩形.BACEDF证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∠ABC=∠D,又CE=CD,即AB=CE,∴四边形ABEC是平行四边形.∵∠AFC=2∠D,∴∠AFC=2∠ABC.又∠AFC=∠ABC+∠BAF,∴∠ABC=∠BAF,∴FA=FB.∴四边形ABEC是矩形.BACEDF