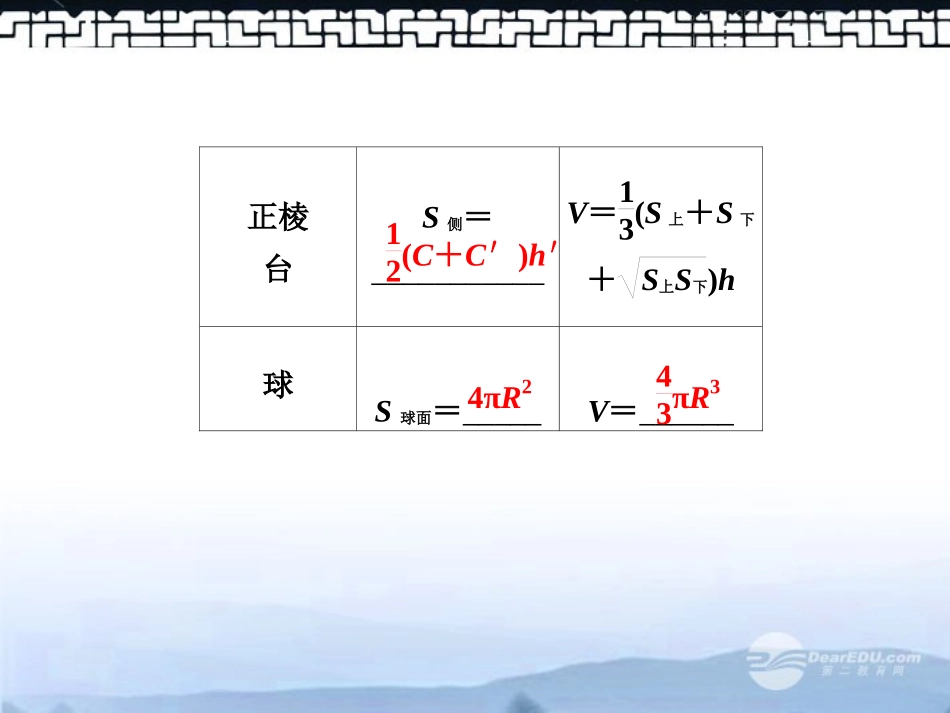
§8.2空间几何体的表面积与体积基础知识自主学习要点梳理1.柱、锥、台和球的侧面积和体积面积体积圆柱S侧=_____V=___=_______圆锥S侧=_____V=_____=______=13πr2l2-r2Shπr2h2πrh13Shπrl13πr2h圆台S侧=________V=13(S上+S下+S上S下)h=13π(r21+r22+r1r2)h直棱柱S侧=____V=____正棱锥S侧=____V=_____π(r1+r2)lChSh12Ch′13Sh正棱台S侧=___________V=13(S上+S下+S上S下)h球S球面=_____V=______12(C+C′)h′4πR243πR32.几何体的表面积(1)棱柱、棱锥、棱台的表面积就是________________.(2)圆柱、圆锥、圆台的侧面展开图分别是_______、________、________;它们的表面积等于__________________________.各面面积之和矩形扇形扇环形侧面积与底面面积之和[难点正本疑点清源]1.几何体的侧面积和全面积几何体侧面积是指(各个)侧面面积之和,而全面积是侧面积与所有底面积之和.对侧面积公式的记忆,最好结合几何体的侧面展开图来进行.要特别留意根据几何体侧面展开图的平面图形的特点来求解相关问题.如直棱柱(圆柱)侧面展开图是一矩形,则可用矩形面积公式求解.再如圆锥侧面展开图为扇形,此扇形的特点是半径为圆锥的母线长,圆弧长等于底面的周长,利用这一点可以求出展开图扇形的圆心角的大小.2.要注意领会和掌握两种数学思想方法:割补法与等积法割补法是割法与补法的总称.补法是把不规则(不熟悉的或复杂的)几何体延伸或补成规则的(熟悉的或简单的)几何体,把不完整的图形补成完整的图形.割法是把复杂的(不规则的)几何体切割成简单的(规则的)几何体.割与补是对立统一的,是一个问题的两个相反方面.割补法无论是求解体积问题还是求解空间角(或空间距离)以及证明垂直或平行关系都有简化解题过程、开阔思维的优点.等积法包括等面积法和等体积法.等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到,利用等积法可以用来求解几何图形的高或几何体的高,特别是在求三角形的高和三棱锥的高.这一方法回避了具体通过作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.基础自测1.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为.解析设圆锥的母线为l,圆锥底面半径为r.则12πl2+πr2=3π,πl=2πr,∴r=1,即圆锥的底面直径为2.22.所有棱长为1的正三棱锥的全面积为.解析S=4×34×12=3.33.如图所示,在棱长为4的正方体ABCD—A1B1C1D1中,P是A1B1上一点,且PB1=14A1B1,则多面体P—BCC1B1的体积为.解析 四棱锥P—BB1C1C的底面积为16,高PB1=1,∴VP—BB1C1C=13×16×1=163.1634.若正方体的棱长为2,则以该正方体各个面的中心为顶点的凸多面体的体积为()A.26B.23C.33D.23解析由题意可知,此几何体是由同底面的两个正四棱锥组成的,底面正方形的边长为1,每一个正四棱锥的高为22,所以V=2×13×1×22=23.B5.(2010·全国)设长方体的长、宽、高分别为2a、a、a,其顶点都在一个球面上,则该球的表面积为()A.3πa2B.6πa2C.12πa2D.24πa2解析由于长方体的长、宽、高分别为2a、a、a,则长方体的体对角线长为(2a)2+a2+a2=6a.又长方体外接球的直径2R等于长方体的体对角线,∴2R=6a.∴S球=4πR2=6πa2.B题型分类深度剖析题型一几何体的展开与折叠例1有一根长为3πcm,底面半径为1cm的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,并使铁丝的两个端点落在圆柱的同一母线的两端,求铁丝的最短长度为多少?思维启迪:把圆柱沿这条母线展开,将问题转化为平面上两点间的最短距离.解把圆柱侧面及缠绕其上的铁丝展开,在平面上得到矩形ABCD(如图所示),由题意知BC=3πcm,AB=4πcm,点A与点C分别是铁丝的起、止位置,故线段AC的长度即为铁丝的最短长度.AC=AB2+BC2=5πcm,故铁丝的最短长度为5πcm.探究提高求立体图形表面上两点的最短距离问题,是立体几何中的一个重要题型.这类题目的特点是:立体图形的性质和数量关系分散在立体图形的几个平面上或旋转体的侧面上.为了便于发现它们图形间性质与数量上的相互关系,必须将图中的某些平面旋转到同一平面上,或者将曲面展开为平面,使问题得到解决.其基本步...