根与系数关系.2.4一元二次方程根与系数的关系(1)VIP免费

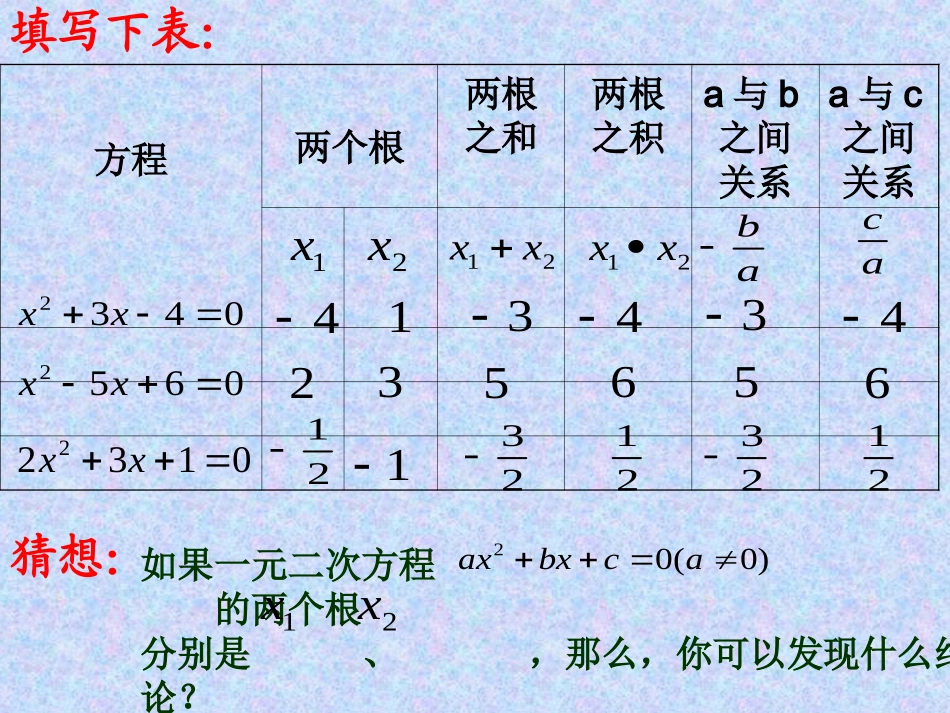
人教课标九上·§22.3(2)1.一元二次方程的一般形式是什么？3.一元二次方程的根的情况怎样确定？2.一元二次方程的求根公式是什么？)0(02acbxaxacb42没有实数根两个相等的实数根两个不相等的实数根000)04(2422acbaacbbx填写下表：方程两个根两根之和两根之积a与b之间关系a与c之间关系1x2x21xx21xxabac猜想：如果一元二次方程的两个根分别是、，那么，你可以发现什么结论？)0(02acbxax1x2x0432xx0652xx01322xx23212123214656531213434已知：如果一元二次方程的两个根分别是、.abxx21acxx21)0(02acbxax1x2x求证：推导:aacbbaacbbxx24242221aacbbacbb24422ab22abaacbbaacbbxx2424222122244aacbb244aacac如果一元二次方程的两个根分别是、，那么：abxx21acxx21)0(02acbxax1x2x这就是一元二次方程根与系数的关系，也叫韦达定理.1、下列方程中，两根的和与两根的积各是多少？013.12xx223.22xx032.32xxxx214.42一、根与系数的关系的直接应用1、设x1、x2是方程利用根与系数的关系，求下列各式的值：的根03422xx11).1(21xx2112).2(xxxx二、根与系数的关系的间接应用2、利用根与系数的关系，求一元二次方程两个根的；（1）平方和；（2）倒数和01322xx解：设方程的两个根是x1x2，那么32123112413212232121,2321212122221212212121xxxxxxxxxxxxxxxx∵3：已知方程x2＝2x＋1的两根x1,x2，不解方程，求下列各式的值.（1）（x1－x2）2（2）x13x2＋x1x23（3）212112xxxx2.应用一元二次方程的根与系数关系时，首先要把已知方程化成一般形式.3.应用一元二次方程的根与系数关系时，要特别注意，方程有实根的条件，即在初中代数里，当且仅当时，才能应用根与系数的关系.1.一元二次方程根与系数的关系是什么?042acb1.已知方程的一个根是2，求它的另一个根及k的值.0652kxx2.方程的两根互为倒数，求k的值.01232kkxx作业补充规律：两根均为负的条件：X1+X2且X1X2.两根均为正的条件：X1+X2且X1X2.两根一正一负的条件：X1+X2且X1X2.当然，以上还必须满足一元二次方程有根的条件：b2-4ac≥0引申:1、若ax2bxc0(a00)（1）若两根互为相反数,则b0;（2）若两根互为倒数,则ac;（3）若一根为0,则c0;（4）若一根为1,则abc0;（5）若一根为1,则abc0;（6）若a、c异号,方程一定有两个实数根.