1.2.1常见函数的导数VIP免费

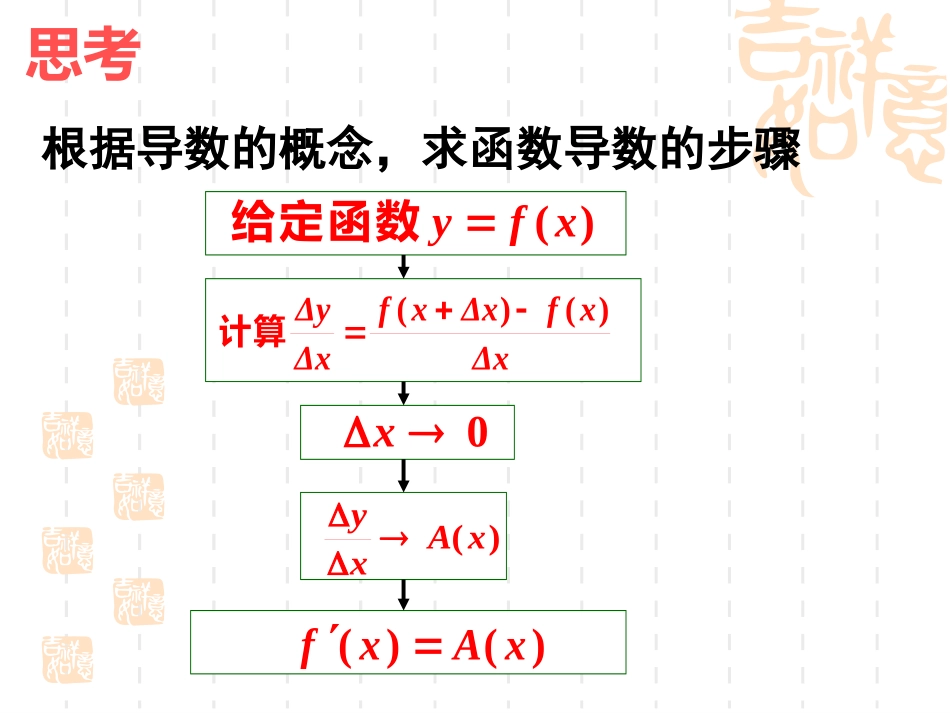
常见函数的导数常见函数的导数江阴市澄西中学江阴市澄西中学卞小俊卞小俊复习回顾上任一点都可导在若函数),()(baxfy)(xfyxxx00,1、函数在区间上的平均变化率；4、导函数;记作：xxfxxf)()(002、如何得到瞬时变化率？,0时当x常数）()()(00Axxfxxf处的导数在即函数0)(xxxf3、导数的几何意义？)(0xf)(0xf记作：处的切线的斜率在点曲线))(,()(00xfxPxfy)(xf思考根据导数的概念，求函数导数的步骤)(xfy给定函数xΔxfxΔxfxΔyΔ)()(计算0x)(xAxy)()(xAxf根据导数的定义可以得出一些常见函数的导数公式.求函数（，为常数）的导数.0b特别地：kbkxxf)()(（b为常数）bkxxf)(kb,21xy23xyxy2求下列函数的导数求下列函数的导数xxfxxfxxfxxf)()4(1)()3()()2()()1(32合作探究21xy1)()3(xxf21)()4(xxf2xy2121xy建构数学以上求导公式可以归纳如下：以上求导公式可以归纳如下：xxxxxxxxxbbbkkbkx21)7(1)1)(6(3))(5(2))(4(1)(3(02,()(12232）（为常数））（为常数））（基本初等函数的导数：基本初等函数的导数：)())(8(1为常数ααxxααxxcos))(sin13(xxsin))(cos14(1)0(11)()10(a,axlnaelogxxlogaa且))(11(eexxxlnx1)(12)(1)0,(ln))(9(aaaaaxx且数学运用求下列函数的导数:5)1(xyxy4)2(xxy)3(xy3log)4()2cos()5(xπy6sin)6(yxycos)7()1()8(fy.)0,1(ln:处的切线方程在点求曲线例Pxy.,ln21的值求的一条切线是曲线变式：若直线bxybxy课堂小结：今天你有何收获今天你有何收获??（（11）基本初等函数的导数公式）基本初等函数的导数公式（（22）能结合其几何意义解决一）能结合其几何意义解决一些与切点、切线斜率有关的简单些与切点、切线斜率有关的简单应用问题应用问题..当堂检测.,15的值和切点的坐标求图象的切线为函数、若直线bxybxy___________)3,1(34______)02(cos3_________)1(,log)(2__________,1243处的切线方程为在点、曲线处切线的倾斜角为，在点、曲线则、已知则它的导函数为、设xyπxyfxxfxy4143x2ln1π4333ln3)3(ln3xy2)11(2)1,1(bb时，，当切点为时，当切点为作业：作业：教材教材P20.P20.第第2,3,4,62,3,4,6