1.3.2余弦函数、正切函数的图象与性质VIP免费

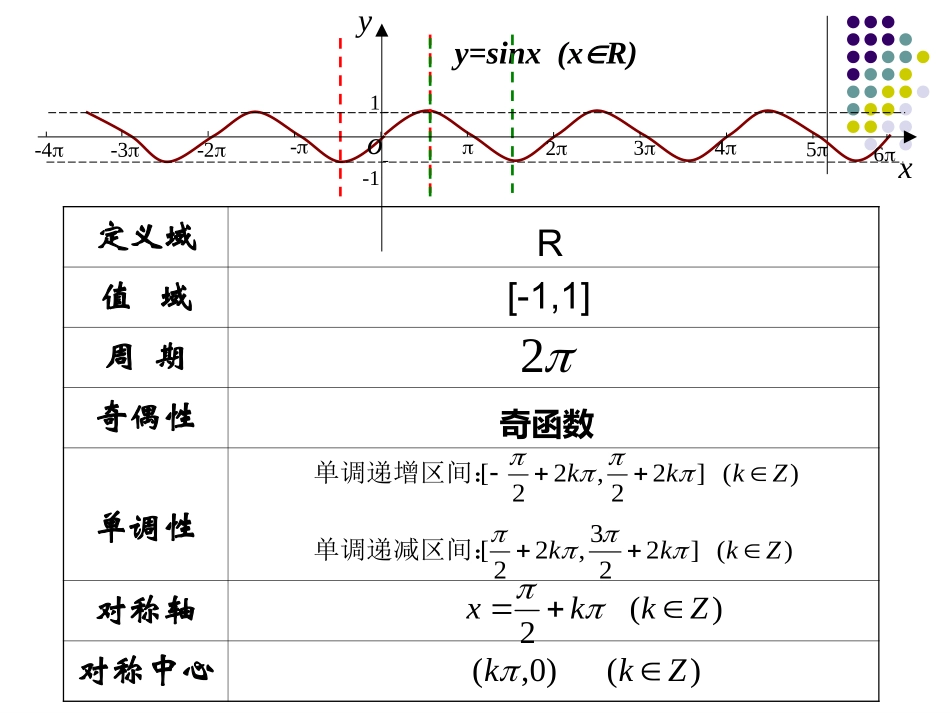
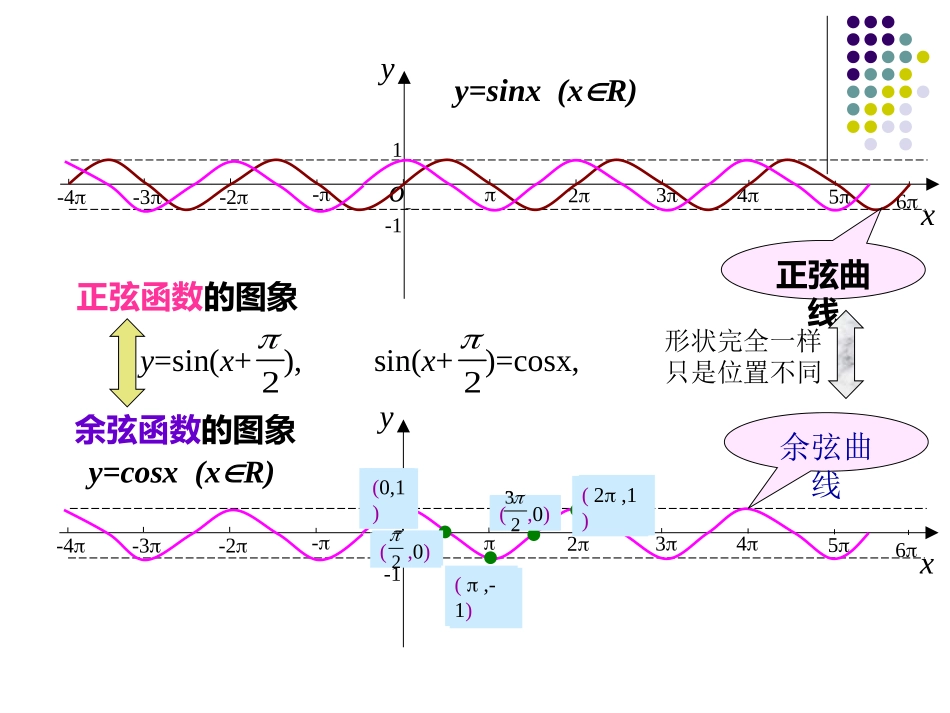
余弦函数的图象与性质定义域值域周期奇偶性单调性对称轴对称中心R[-1,1]2)(]223,22[)(]22,22[ZkkkZkkk单调递减区间：单调递增区间：)(2Zkkx)()0,(Zkk奇函数y=sinx(xR)x6yo--12345-2-3-41x6yo--12345-2-3-41余弦函数的图象正弦函数的图象x6yo--12345-2-3-41y=sin(x+),2余弦曲线(0,1)(,0)2(,-1)(,0)23(2,1)正弦曲线形状完全一样只是位置不同(0,1)(,0)2(,-1)(,0)23(2,1)y=sinx(xR)y=cosx(xR)sin(x+)=cosx,2yxo1-122322如何作出正弦函数的图象（在精确度要求不太高时）？(0,0)(,1)2(,0)(,-1)23(2,0)五点画图法y--1-12o46246--定义域值域周期奇偶性单调性对称轴对称中心R[-1,1]2)(]22,2[)(]2,2[ZkkkZkkk单调递增区间：单调递减区间：)(Zkkx)()0,2(Zkk偶函数y=cosx(xR)x=2kπ时ymax=1x=2kπ+π时ymin=-1函数性质y=sinx(kz)∈y=cosx(kz)∈定义域值域最值及相应的x的集合周期性奇偶性单调性对称中心对称轴RR[-1,1][-1,1]x=2kπ时ymax=1x=2kπ+π时ymin=-1周期为T=2π周期为T=2π奇函数偶函数在x[2kπ-π∈，2kπ](kz)∈上都是增函数。在x[2kπ∈，2kπ+π](kz)∈上都是减函数,(kπ,0)x=kπx=2kπ+时ymax=1x=2kπ-时ymin=-1π2π2在x[2kπ-,2kπ+]∈(kz)∈上都是增函数在x[2kπ+∈,2kπ+](kz)∈上都是减函数.π2π2π23π2(kπ+,0)π2x=kπ+π2例1、求下列函数的最大值和最小值以及相应的x值：1cos3)1(xy3)21(cos)2(2xy的集合。大值和最小值的写出使这个函数取得最分别的最大值和最小值，并练习：求函数x3xcos-2y).(63),Z(2333cos213cos).(6),Z(2313cos213cosZkkxkkxxyxZkkxkkxxyx即，此时取得最大值时，取得最小值当即，此时取得最小值时，取得最大值解：当例2、判断下列函数的奇偶性：(1)y=cosx+2(2)y=sinx·cosx的周期。、求函数例)431cos(23xy小结：.2)0,0,,)()(cos(TAARxxAy的周期为为常数，且其中一般地，余弦型函数的性质、研究函数例)33cos(24xy探究1：函数的周期性探究2：函数的单调区间探究3：函数的值域以及函数取得最值时相应的x的值探究4：它的图像是由函数y=cosx的图像经过怎样的变换得到的？函数性质y=sinx(kz)∈y=cosx(kz)∈定义域值域最值及相应的x的集合周期性奇偶性单调性对称中心对称轴RR[-1,1][-1,1]x=2kπ时ymax=1x=2kπ+π时ymin=-1周期为T=2π周期为T=2π奇函数偶函数在x[2kπ-π∈，2kπ](kz)∈上都是增函数。在x[2kπ∈，2kπ+π](kz)∈上都是减函数,(kπ,0)x=kπx=2kπ+时ymax=1x=2kπ-时ymin=-1π2π2在x[2kπ-,2kπ+]∈(kz)∈上都是增函数在x[2kπ+∈,2kπ+](kz)∈上都是减函数.π2π2π23π2(kπ+,0)π2x=kπ+π2