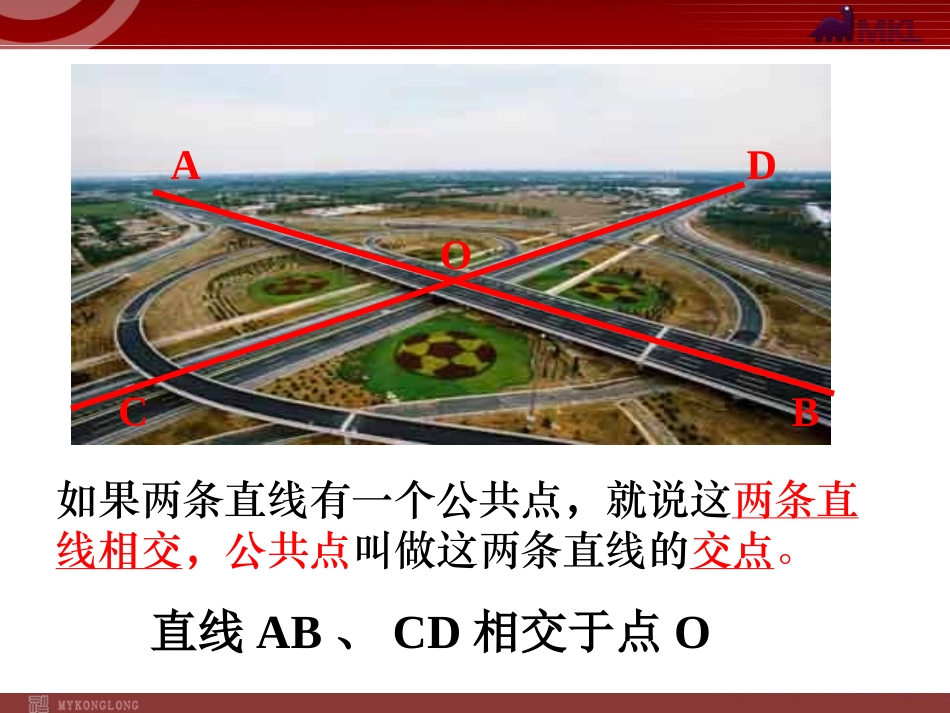
5.1.1相交线1、了解邻补角、对顶角的概念2、能找出图形中的一个角的邻补角和对顶角,3、理解对顶角相等,并能运用它解决一些问题。重点:邻补角、对顶角的概念,对顶角性质与应用。难点:理解对顶角相等的性质的探索。二、重点和难点一、学习目标ABCDO直线AB、CD相交于点O如果两条直线有一个公共点,就说这两条直线相交,公共点叫做这两条直线的交点。握紧把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小直到剪开布片。如果把剪刀的构造看作两条相交的直线相交的直线,这就关系到两条相交直线所成的角的问题。讨论:1、每对角中两个角的位置有怎样的关系?2、这两条直线相交得到哪几对角?2、试根据它们的位置和度数的关系将这几对角进行分类BACDO12343、分别用量角器量一量4个交角的度数,各类角的度数有什么关系?观察:1、两条直线相交组成几个角?两直线相交所形成的角分类OABCD)(1342)(∠3∠1∠2∠4∠1和∠24∠2和∠∠和∠∠和∠14343∠1和∠3∠和∠2任意画两条相交直线任意画两条相交直线,,在形成的四个角在形成的四个角((如图如图))中中,,两两相交共组成几对角?各对角存在怎样的位置关两两相交共组成几对角?各对角存在怎样的位置关系系??OABCD)(1342)(邻补角(邻补角(11):):两条直线相交所两条直线相交所构成的四个角中构成的四个角中,,有公共顶点且有公共顶点且有一条公共边的两个角是邻补角有一条公共边的两个角是邻补角..如∠1与∠2有公共顶点O,有一条公共边OC,所以∠1和∠2是互为邻补角.邻补角(邻补角(22):):邻补角也可以看成是一条直线与端点在一条直线上的一条射线组成的两个角。如∠1与∠2有关概念:有关概念:1、下列图中的∠1与∠2是邻补角吗?为什么?1221(1)(2)否是邻补角的特点:1、顶点相同,2、有一条公共边,另一边互为反向延长线,3、是成对出现的。做一做OABCD)(1342)(对顶角(对顶角(11):):如果一个角的两如果一个角的两边是另一个角的两边的反向延长边是另一个角的两边的反向延长线,那么这两个角互为对顶角。线,那么这两个角互为对顶角。对顶角(对顶角(22):):两条直线相交所构成的四个角中,两条直线相交所构成的四个角中,有公共顶点但没有公共边的两个角是对顶角。有公共顶点但没有公共边的两个角是对顶角。∠1的两边OA、OC分别是∠3的两边OB、OD的反向延长线,所以∠1和∠3是对顶角。∠1的两边是OA和OC,∠3的两边是OB和OD,它们有公共顶点O,但没有公共边,所以∠1和∠3是对顶角,∠1和∠2有一边OC是公共的,所以∠1和∠2不是对顶角。有关概念:有关概念:2、下列各图中∠1、∠2是对顶角吗?请说明理由。否是否否(1)(2)(3)(4)12121212对顶角的特点:1、顶点相同,2、角的两边互为反向延长线,3、是成对出现的。对顶角相等对顶角相等..OABCD)(1342)(已知:直线已知:直线ABAB与与CDCD相交于相交于OO点点((如图如图),),说明说明∠1=∠3、∠2=∠4的理由解:因为直线解:因为直线ABAB与与CDCD相交于相交于OO点点,,所以∠1+∠2=180°、∠2+∠3=180°所以∠1=∠3同理可得:∠2=∠4对顶角的性质对顶角的性质::1、若∠1与∠2是对顶角,∠1=160,则∠2=______0;若∠3与∠4是邻补角,则∠3+∠4=______01801802、若∠1与∠2为对顶角,∠1与∠3互补,则∠2+∠3=0163、要测量两堵围墙所形成的角AOB的度数,但人不能进入围墙,如何测量?CDC练一练例1如图,直线a、b相交。∠1=40o,求∠2,∠3,∠4的度数。ba1234∠2=180°-∠1=180°-40°解:由邻补角的定义,可得=140°由对顶角相等,可得∠3=∠1=40°∠4=∠2=140°若∠1+∠3=50°,求各角的度数。若∠1=m°,求各角的度数。例题讲解2、如图,若∠1:∠2=2:7,求各角的度数。ba1234解:设∠1=2x°,则∠2=7x°根据邻补角的定义,得2x+7x=180x=20则∠1=40°,2=140∠°根据对顶角相等,得∠3=40°,4=140∠°例题讲解2、右图是对顶角量角器,你能说出用它测量角的原理吗?×√××答:对顶角相等。练习与反馈练习与反馈3、如图1,∠2与∠3互为邻补角,∠1=∠2,则∠1与∠3的关系为。互补AEDCB132图14、如图2,三条直线a...