九年级数学上册 13 正方形的性质与判定拓展训练(新版)北师大版试卷VIP专享VIP免费

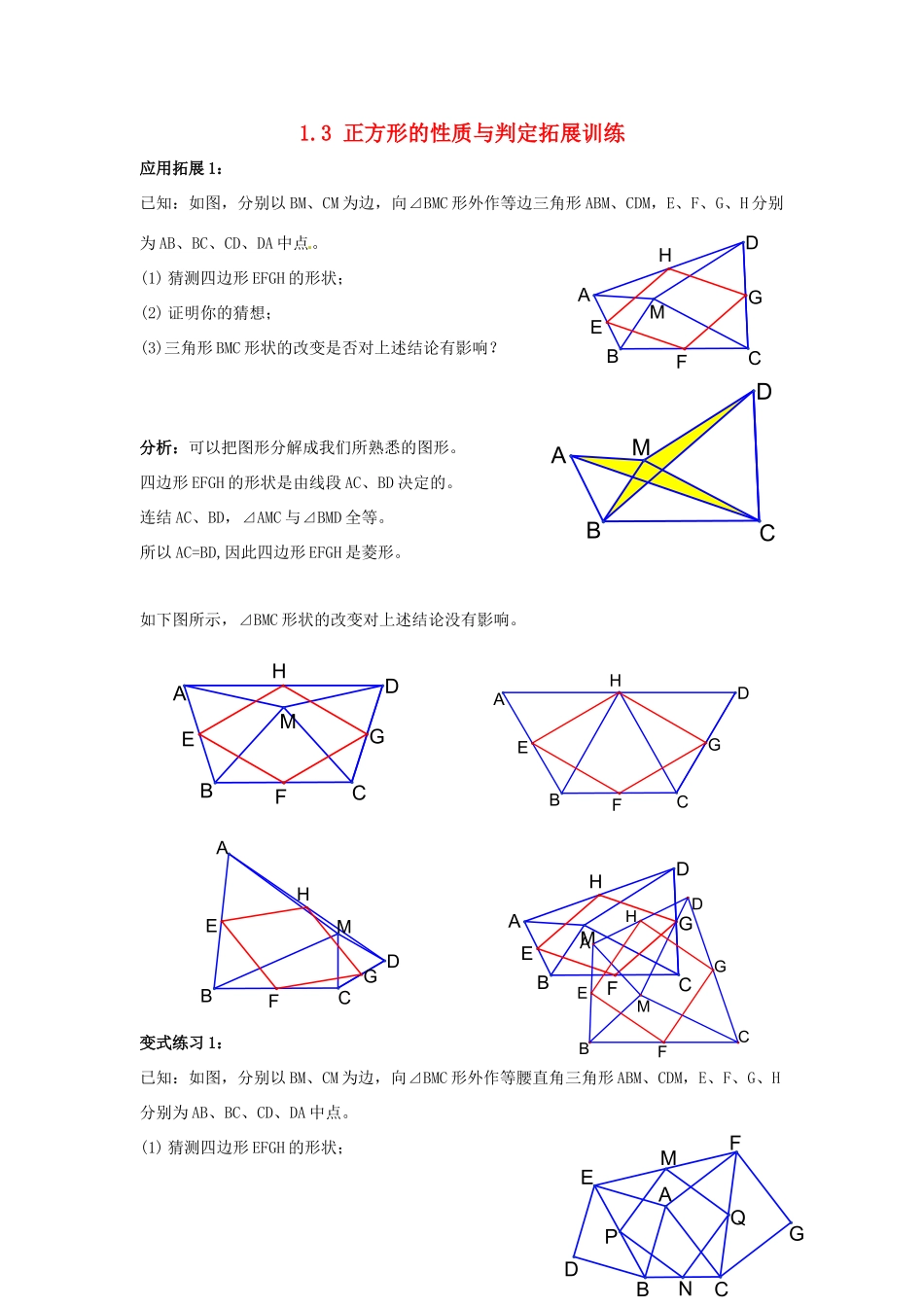
1.3正方形的性质与判定拓展训练应用拓展1：已知：如图，分别以BM、CM为边，向⊿BMC形外作等边三角形ABM、CDM，E、F、G、H分别为AB、BC、CD、DA中点。(1)猜测四边形EFGH的形状；(2)证明你的猜想；(3)三角形BMC形状的改变是否对上述结论有影响？分析：可以把图形分解成我们所熟悉的图形。四边形EFGH的形状是由线段AC、BD决定的。连结AC、BD，⊿AMC与⊿BMD全等。所以AC=BD,因此四边形EFGH是菱形。如下图所示，⊿BMC形状的改变对上述结论没有影响。变式练习1：已知：如图，分别以BM、CM为边，向⊿BMC形外作等腰直角三角形ABM、CDM，E、F、G、H分别为AB、BC、CD、DA中点。(1)猜测四边形EFGH的形状；HGFEDAMCBDAMCBHGFEDAMCBHGFEDACBHGFEDAMCBHGFEDAMCBNMQPFGEDBCAGHDFEAMBC(2)证明你的猜想；（3三角形BMC形状的改变是否对上述结论有影响？变式练习2：已知：如图，分别以AB、AC为边向⊿ABC形外作正方形ABDE、正方形ACGF，M、N、P、Q分别是EF、BC、EB、FC的中点。(1)猜测四边形MPNQ的形状；(2)试证明你猜想的结论。（3）⊿ABC形状的改变是否对上述结论有影响？应用拓展2：如图，四边形ABCD中，（1）若E、F、G、H分别为各边的中点，则四边形EFGH为平行四边形（2）若E、F、G、H分别为各边的四等份点，则四边形EFGH为平行四边形（3）若E、F分别AB、BC边的四等份点，G，H分别为边CD、DA的中点，则四边形EFGH为梯形。应用拓展3：如图，梯形ABCD中，AB∥CD，M是AD中点，N是BC中点，E是CD中点，F是AB中点。求证：若EF=MN，则BD⊥ME。变式练习1：求证：若AC=BD，则EF⊥MN；ABCDHEFGABCDEFGHABCDGHEFABCDFMNBCDAHGFE变式练习2：求证：若AC⊥BD，则EF=MN。应用拓展4：中点三角形的概念：顺次连结三角形的各边中点所组成的三角形叫做中点三角形我们可以得到以下结论：（1）DE=21BC，DF=21AC，EF=21AB（2）△ABC∽△DEF（3）C△DEF=21C△ABC（4）S△DEF=41S△ABC请你模仿上面题目，解答下面的题目：中点四边形的概念：顺次连结四边形的各边中点所组成的四边形叫做中点四边形。我们可以得到以下结论：（1）EF=HG=21AC，EH=FG=21BD（2）四边形EFGH是平行四边形（3）CEFGH=AC+BD（4）SEFGH=21SABCD拓展（1）：中点五边形呢？拓展（2）：中点六边形呢？拓展（3）：中点n边形呢？1ABSDEF=14SABCBADCEF