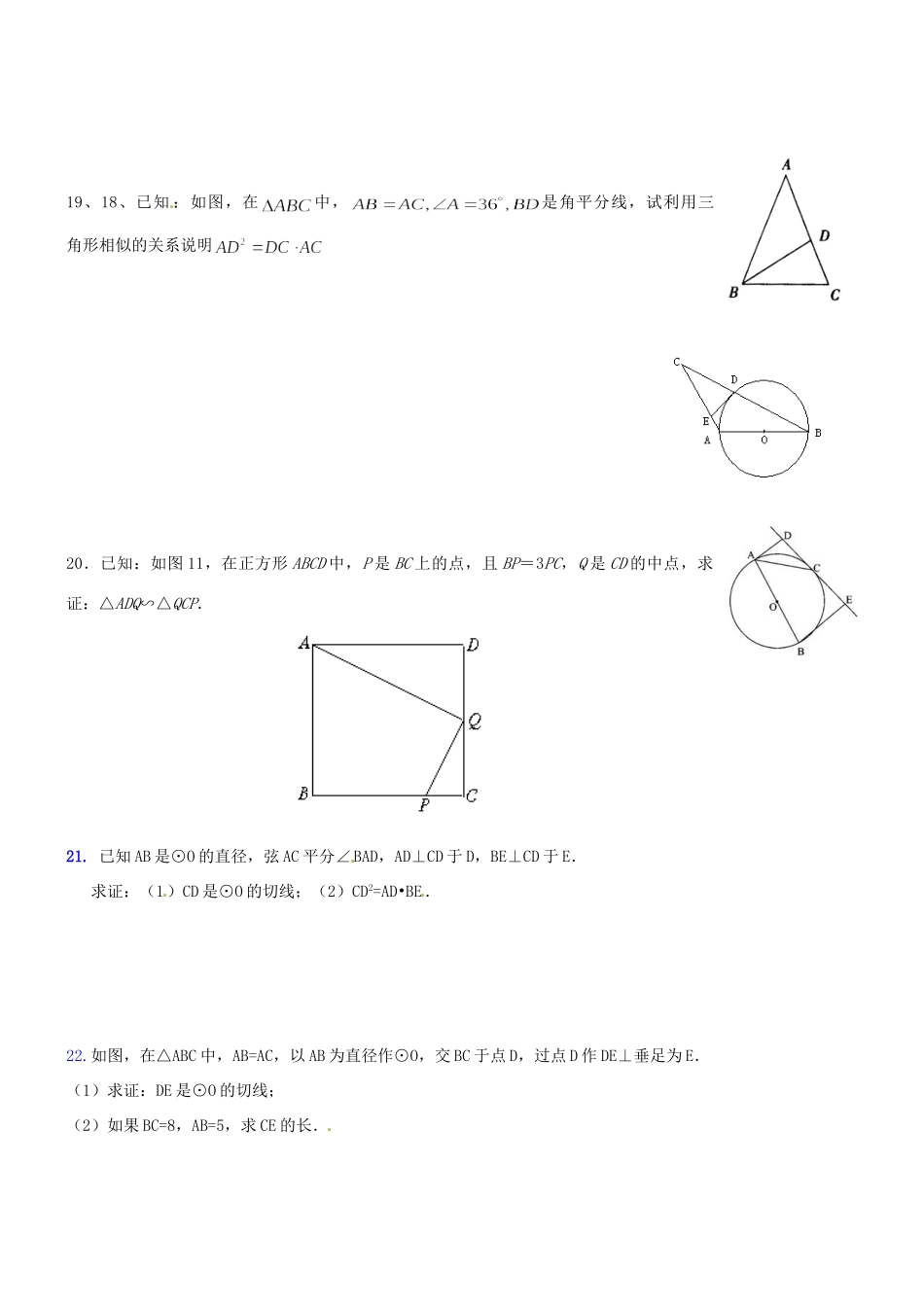
甘肃省民勤县第五中学九年级数学上册《相似三角形》测试题新人教版一选择题:1、下列命题中正确的是()①三边对应成比例的两个三角形相似②二边对应成比例且一个角对应相等的两个三角形相似③一个锐角对应相等的两个直角三角形相似④一个角对应相等的两个等腰三角形相似A、①③B、①④C、①②④D、①③④2、如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是()ABCD3、如图,D、E分别是AB、AC上两点,CD与BE相交于点O,下列条件中不能使ΔABE和ΔACD相似的是()A.∠B=∠CB.∠ADC=∠AEBC.BE=CD,AB=ACD.AD∶AC=AE∶AB4、在矩形ABCD中,E、F分别是CD、BC上的点,若∠AEF=90°,则一定有()AΔADE∽ΔAEFBΔECF∽ΔAEFCΔADE∽ΔECFDΔAEF∽ΔABF5、如图,E是平行四边形ABCD的边BC的延长线上的一点,连结AE交CD于F,则图中共有相似三角形()A1对B2对C3对D4对二、填空:6.如图,P为线段AB上一点,AD与BC交干E,∠CPD=∠A=∠B,BC交PD于E,AD交PC于G,则图中相似三角形有()7、如图,A、B、C、D是⊙O上的四个点,AB=AC,AD交BC于点E,AE=3,ED=4,则AB的长为()8.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB=9.数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为1.2米,落在地面上的影长为2.4米,则树高为10、如图,已知AB是⊙O的直径,C是AB延长线上一点,BC=OB,CE是⊙O的切线,切点为D,过点A作AE⊥CE,垂足为E,则CD:DE的值是()11、已知线段a=4cm,b=9cm,则线段a、b的比例中项为______cm12、已知⊿ABC的三边长分别为,,2,⊿A′B′C′的两边长分别是1和,如果⊿ABC与⊿A′B′C′相似,那么⊿A′B′C′的第三边长应该是13、如图,□ABCD中,EF∥AB,DE∶EA=2∶3,EF=4,则CD的长()14、在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,若要在AB上找一点E,使△ADE与原三角形相似,那么AE=15、如图,在△ABC中,点D在AB上,请再添一个适当的条件,使△ADC∽△ACB,那么可添加的条件是三、解答题:16、如图,ΔABC与ΔADB中,∠ABC=∠ADB=90°,AC=5cm,AB=4cm,如果图中的两个直角三角形相似,求AD的长.17、如图,在中,,BD平分,试说明:AB·BC=AC·CD18、如图,(1)∽吗?说明理由。(2)求AD的长。19、18、已知:如图,在中,是角平分线,试利用三角形相似的关系说明20.已知:如图11,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.21.已知AB是⊙O的直径,弦AC平分∠BAD,AD⊥CD于D,BE⊥CD于E.求证:(1)CD是⊙O的切线;(2)CD2=AD•BE.22.如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,过点D作DE⊥垂足为E.(1)求证:DE是⊙O的切线;(2)如果BC=8,AB=5,求CE的长.23.如图,为了求出海岛上的山峰AB的高度,在D和F处树立标杆DC和FE,标杆的高都是3丈,相隔1000步(1步等于5尺),并且AB、CD和EF在同一平面内,从标杆DC退后123步的G处,可看到山峰A和标杆顶端C在一直线上,从标杆FE退后127步的H处,可看到山峰A和标杆顶端E在一直线上.求山峰的高度AB及它和标杆CD的水平距离BD各是多少?(古代问题)