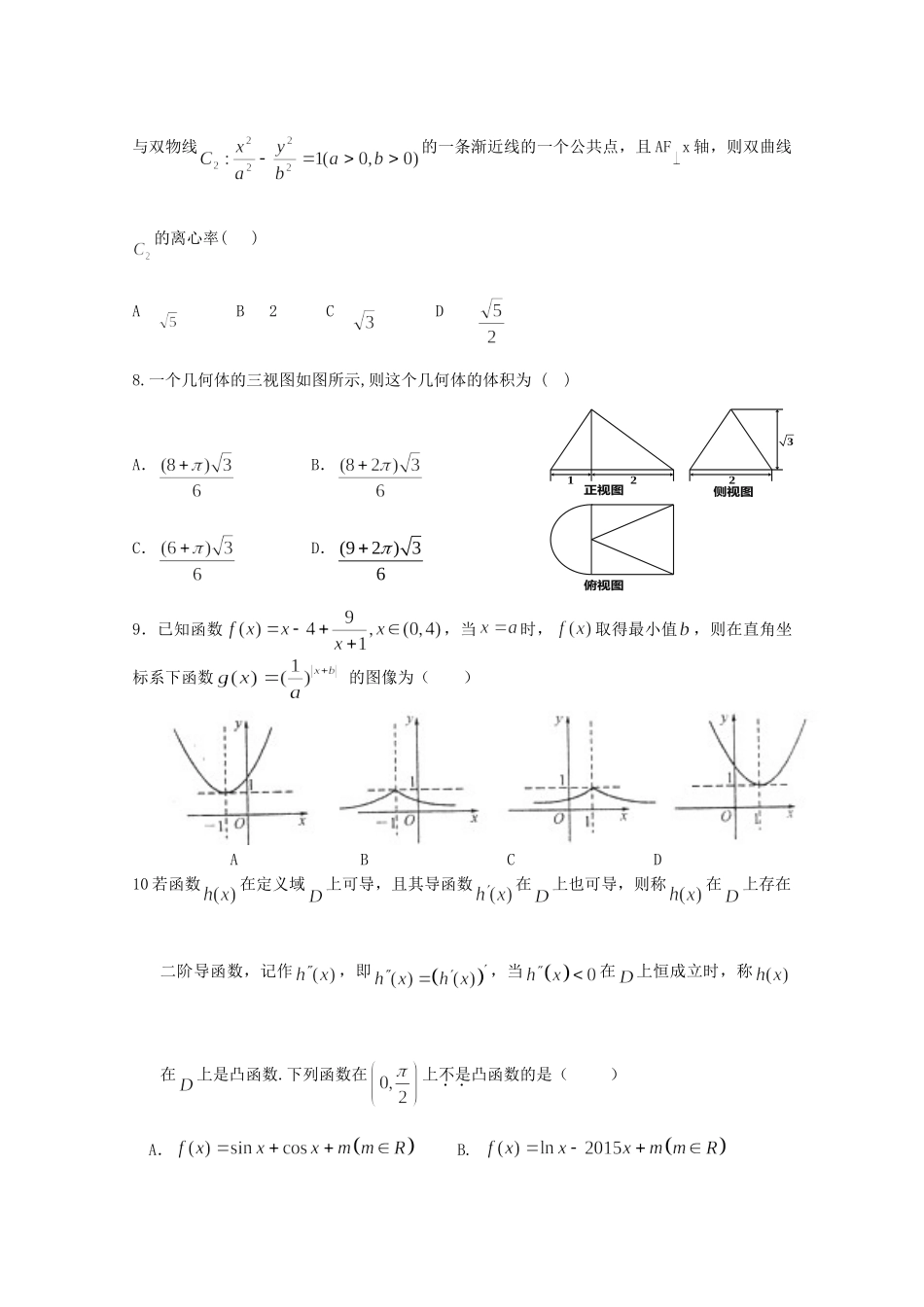
高三数学(文科)(考试时间:120分钟总分:150分)第Ⅰ卷(选择题50分)一、选择题:本大题共1小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的。1.函数的定义域是()A.B.C.D.2.函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的最小正周期为π,且其图象向右平移个单位后得到的函数为奇函数,则函数f(x)的图象()A.关于点(,0)对称B.关于点(,0)对称C关于直线x=对称D关于直线x=对称3已知点P在抛物线y2=4x上,点M在圆(x﹣3)2+(y﹣1)2=1上,点N坐标为(1,0),则|PM|+|PN|的最小值为()A.5B.4C.3D.+14.已知函数,在下列区间中,包含的零点的区间是()A.B.C.D.5.已知满足,则的最大值为()A.B.C.D.6.设、是两个不同的平面,、为两条不同的直线,命题:若平面∥,,,则∥;命题:∥,⊥,,则⊥,则下列命题为真命题的是()A.或B.且C.或D.且7设F是抛物线的焦点,点A是抛物线与双物线的一条渐近线的一个公共点,且AFx轴,则双曲线的离心率()AB2CD8.一个几何体的三视图如图所示,则这个几何体的体积为()A.B.C.D.(92)369.已知函数,当时,取得最小值,则在直角坐标系下函数的图像为()ABCD10若函数在定义域上可导,且其导函数在上也可导,则称在上存在二阶导函数,记作,即,当在上恒成立时,称在上是凸函数.下列函数在上不是凸函数的是()A.B.3122正视图侧视图俯视图C.D.第Ⅱ卷(非选择题共100分)二、填空题:本大题共58小题,每小题5分,共25分,把答案填在答题卷的相应位置11若等比数列的各项均为正数,且,则.12已知函数f(x)满足f(x)=2f(),当x∈[1,+∞)时,f(x)=lnx,若在区间(0,e2)内,函数g(x)=f(x)﹣ax与x轴有3个不同的交点,则实数a的取值范围是13已知a函数的图像过(0,1)点,则的最小值是14.若为双曲线的渐近线方程,则=15.给出下列命题:①若y=f(x)是奇函数,则y=|f(x)|的图象关于y轴对称;②若函数f(x)对任意x∈R满足f(x)•f(x+4)=1,则8是函数f(x)的一个周期③若logm3<logn3<0,则0<m<n<1;④若f(x)=e|x﹣a|在[1,+∞)上是增函数,则a≤1.其中正确命题的序号是_________.三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.16(本题满分12分)已知向量)sin,sin(cos),cos2,sin(cosxxxnxxxm。(1)求nmxf)(的最小正周期和单调减区间;(2)将函数)(xfy的图象向右平移8个单位,再将所得图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数)(xgy的图象,在△ABC中,角A、B、C的对边分别为cba,,,若2,22)B(,0)2A(bgf,求a的值.17.(本小题满分12分)如图2,在三棱柱中,平面,,,,、分别为、的中点.(Ⅰ)求证:平面;(Ⅱ)求三棱锥的体积.18(本题满分12分)已知数列的前n项和,数列{}满足,且求设为数列{}的前n项和,求19已知椭圆C:的一个顶点为A(2,0),离心率为,直线y=k(x-1)与椭圆C交于不同的两点M,N.(1)求椭圆C的方程(2)当AMN的面积为时,求k的值20.(本小题满分12分)已知函数,其中,且曲线在点处的切线垂直于直线.(Ⅰ)求的值;(Ⅱ)求函数的单调区间和极值.21.(本小题满分14分)在平面直角坐标系中,椭圆:的离C1B1A1FECBA图2心率为,上顶点在直线上.(I)求椭圆的方程;(II)过原点的直线与椭圆交于,两点(,不是椭圆的顶点).点在椭圆上,且,直线与轴、轴分别交于,两点.(i)设直线,的斜率分别为,,问是否存在实数,使得?若存在,求出的值;若不存在,请说明理由;(ii)求面积的最大值沂水一中12月份高三学情调查数学(文科)参考答案一选择题1C2B3C4C5B6C7A8A9B10D二填空题115012133+14215.①②④三、解答题:16(1)Txxf),432sin(2)()](83,8[Zkkk;(2).(1)..由得:,所以nmxf)(的单调减区间为:)](83,8[Zkkk.(2)将函数)(xfy的图象向右平移8个单位,所得函数为,再将所得图象上各点的横坐标伸长到原来的2倍,纵坐标不变,所得函数为,即.由题设得:.又.由正弦定理得:.17.解:(Ⅰ)法一:取中点,连...