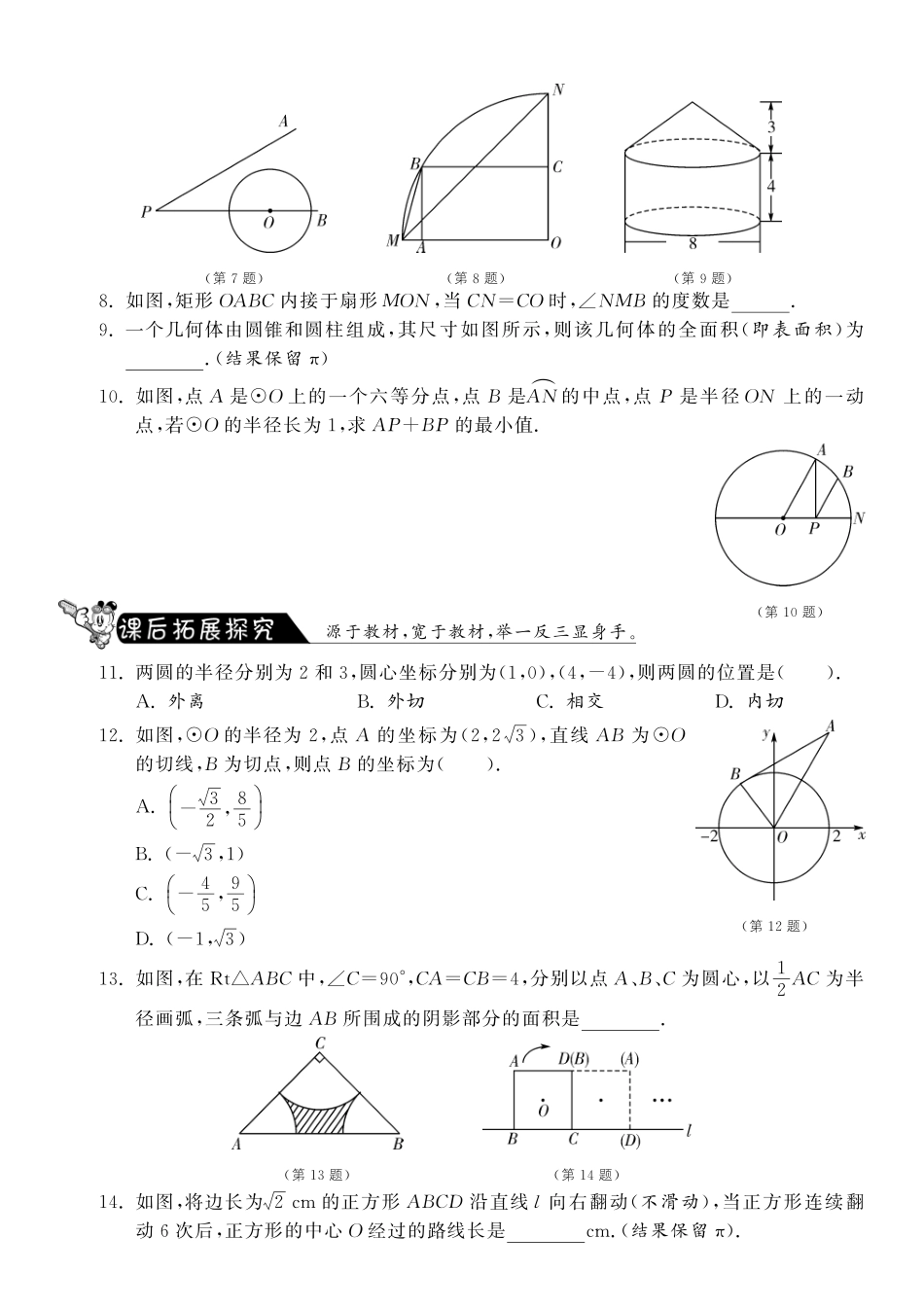
复习课开心预习梳理,轻松搞定基础.圆————圆的基本性质————圆的有关概念————弦—弧—垂径定理—定理:—推论:—圆周角定理————定理:—推论:—圆心角、弦、弧之间的关系————定理:—定理:—与圆有关的位置关系————点与圆的位置关系————点在圆外:即—点在圆上:即—点在圆内:即—直线与圆的位置关系————相离:即—相切:即—圆的切线————判定:—性质:—相交:即—圆与圆的位置关系————外离:即—外切:即—相交:即—内切:即—内含:即—圆的有关计算————弧长、扇形面积————有关概念:—有关公式:—圆锥的面积————有关概念—有关公式重难疑点,一网打尽.1.第三十届奥运会于2012年7月27日在英国伦敦开幕,奥运会旗图案有五个圆环组成,如图也是一幅五环图案,在这个五个圆中,不存在的位置关系是().A.外离B.内切C.外切D.相交(第1题)(第2题)2.如图,为做一个试管架,在acm长的木条上钻了4个圆孔,每个孔的直径为2cm,则x等于().A.a+85cmB.a-165cmC.a-45cmD.a-85cm3.已知AB是☉O的弦,OC⊥AB,垂足为C.若OA=2,OC=1,则AB的长为().A.5B.25C.3D.234.已知AC⊥BC于点C,BC=a,CA=b,AB=c,下列选项中☉O的半径为aba+b的是().5.如图,☉O是△ABC的外接圆,∠BAC=60°,若☉O的半径OC为2,则弦BC的长为().A.1B.3C.2D.23(第5题)(第6题)6.如图,把一个斜边长为2且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是().A.πB.3C.3π4+32D.11π12+347.如图,∠APB=30°,圆心在边PB上的☉O半径为1cm,OP=3cm,若☉O沿BP方向移动,当☉O与PA相切时,圆心O移动的距离为cm.(第7题)(第8题)(第9题)8.如图,矩形OABC内接于扇形MON,当CN=CO时,∠NMB的度数是.9.一个几何体由圆锥和圆柱组成,其尺寸如图所示,则该几何体的全面积(即表面积)为.(结果保留π)10.如图,点A是☉O上的一个六等分点,点B是AN︵的中点,点P是半径ON上的一动点,若☉O的半径长为1,求AP+BP的最小值.(第10题)源于教材,宽于教材,举一反三显身手.11.两圆的半径分别为2和3,圆心坐标分别为(1,0),(4,-4),则两圆的位置是().A.外离B.外切C.相交D.内切(第12题)12.如图,☉O的半径为2,点A的坐标为(2,23),直线AB为☉O的切线,B为切点,则点B的坐标为().A.-32,85æèçöø÷B.(-3,1)C.-45,95æèçöø÷D.(-1,3)13.如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以点A、B、C为圆心,以12AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是.(第13题)(第14题)14.如图,将边长为2cm的正方形ABCD沿直线l向右翻动(不滑动),当正方形连续翻动6次后,正方形的中心O经过的路线长是cm.(结果保留π).15.如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF,则以AC和BC的长为两根的一元二次方程是.(第15题)(第16题)16.如图,已知☉O是以坐标原点O为圆心,1为半径的圆,∠AOB=45°,点P在x轴上运动,若过点P且与OA平行的直线与☉O有公共点,设P(x,0),则x的取值范围是.17.如图所示为圆柱形大型储油罐固定在U型槽上的横截面图.已知图中ABCD为等腰梯形(AB∥DC),支点A与B相距8m,罐底最低点到地面CD距离为1m.设油罐横截面圆心为O,半径为5m,∠D=56°,求:U型槽的横截面(阴影部分)的面积.(参考数据:sin53°≈0.8,tan56°≈1.5,π≈3,结果保留整数)(第17题)18.如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD、CD.(1)求证:BD=CD;(2)请判断B、E、C三点是否在以点D为圆心,以DB为半径的圆上?并说明理由.(第18题)复习课1.B2.D3.D4.C5.D6.D7.18.30°9.68π10.211.B12.D13.8-2π14.33π15.x2-x+1=0(答案不唯一)16.-2≤x≤217.如图,连接AO、BO.过点A作AE⊥DC于点E,过点O作ON⊥DC于点N,ON交☉O于点M,交AB于点F.则OF⊥AB. OA=OB=5m,AB=8m,∴AF...