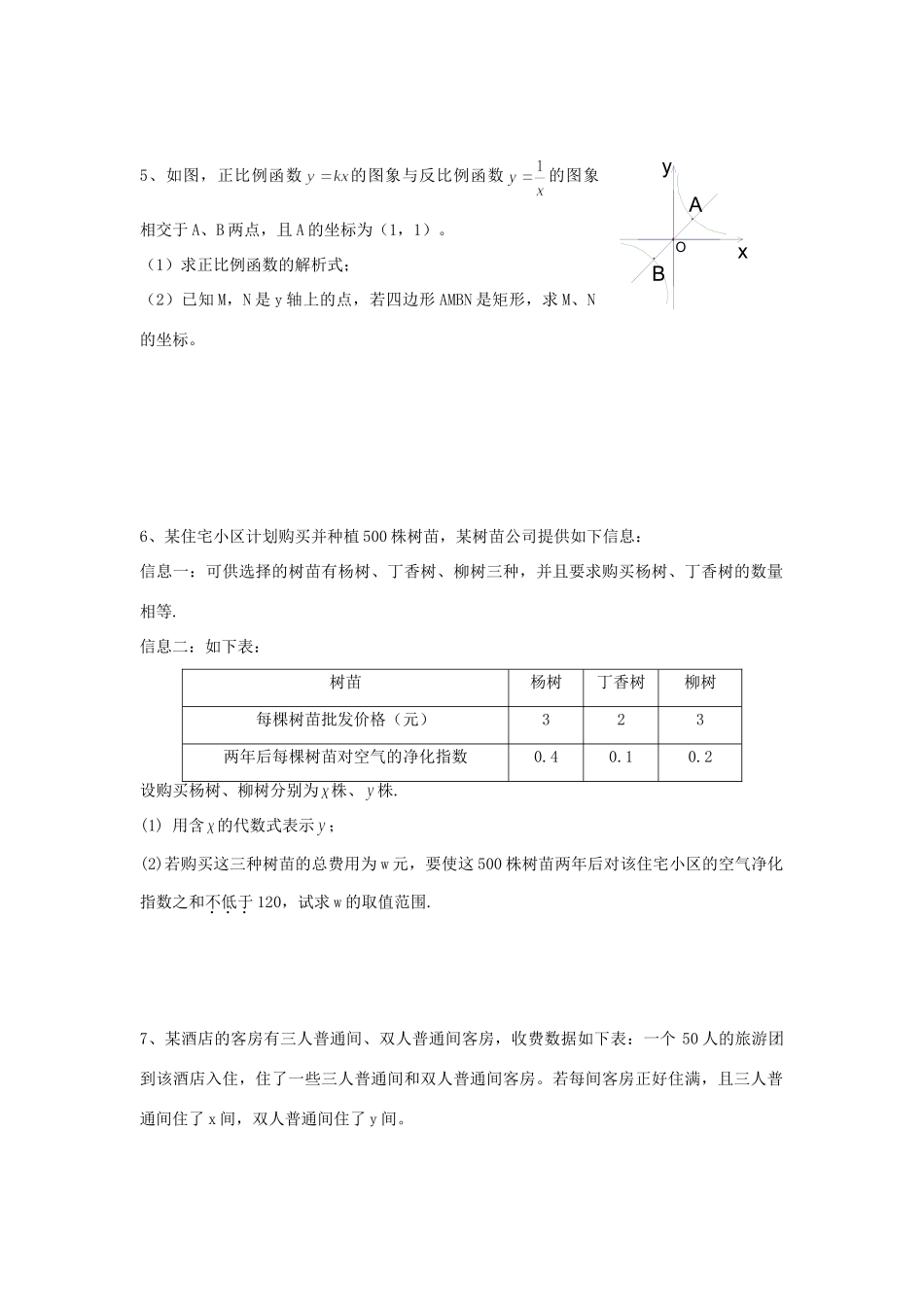
初三数学一次方程组、一次不等式和一次函数综合题1、阅读下面的例题:解方程:解:(1)当≥0时,原方程化为,解得:,(不合题意,舍去).(2)当0时,原方程化为,解得:(不合题意,舍去),∴原方程的根是,.请参照例题解方程,则此方程的根是.2、如图,正比例函数y=x与反比例函数的图象相交于A、C两点,AB轴于B,CD轴于D,则四边形ABCD的面积为.3、如图,一个蓄水桶,60分钟可将一满桶水放干.其中,水位h(cm)随着放水时间t(分)的变化而变化.h与t的函数的大致图像为()4、小明所在学校离家距离为2千米,某天他放学后骑自行车回家,行驶了5分钟后,因故停留10分钟,继续骑了5分钟到家.下面哪一个图象能大致描述他回家过程中离家的距离(千米)与所用时间(分)之间的关系().yxDCBAO(第2题图)5、如图,正比例函数的图象与反比例函数的图象相交于A、B两点,且A的坐标为(1,1)。(1)求正比例函数的解析式;(2)已知M,N是y轴上的点,若四边形AMBN是矩形,求M、N的坐标。6、某住宅小区计划购买并种植500株树苗,某树苗公司提供如下信息:信息一:可供选择的树苗有杨树、丁香树、柳树三种,并且要求购买杨树、丁香树的数量相等.信息二:如下表:树苗杨树丁香树柳树每棵树苗批发价格(元)323两年后每棵树苗对空气的净化指数0.40.10.2设购买杨树、柳树分别为株、株.(1)用含的代数式表示;(2)若购买这三种树苗的总费用为w元,要使这500株树苗两年后对该住宅小区的空气净化指数之和不低于120,试求w的取值范围.7、某酒店的客房有三人普通间、双人普通间客房,收费数据如下表:一个50人的旅游团到该酒店入住,住了一些三人普通间和双人普通间客房。若每间客房正好住满,且三人普通间住了x间,双人普通间住了y间。xyBOA(1)用含x的代数式表示y;(2)若该旅游团一天的住宿费要低于3000元,且旅客要求住进的三人普通间不多于双人普通间,那么该旅游团住进的三人普通间和双人普通间各多少间?8、某超市新进30千克的散装糖果,现决定将其分别用1.5千克和1千克装两种规格包装盒全部包装后再出售,已知这两种规格包装盒每个盒子成本分别为0.8元和0.6元.(1)若用规格为1.5千克包装盒装了x盒;规格为1千克包装盒装了y盒,试用含x的代数式表示y。(2)现超市要求1千克装的糖果数量不少于12千克,设所用包装盒成本共w元,问应怎样设计包装方案,才能使包装成本最低?并求出最低成本是多少元?9、近两年某地外向型经济发展迅速,一些著名跨国公司纷纷落户该地新区,对各类人才需求不断增加,现一公司面向社会招聘人员,其信息如下:[信息一]招聘对象:机械制造类和规划设计类人员共150名.[信息二]工资待遇:机械类人员工资为600元/月,规划设计类人员为1000元/月.设该公司招聘机械制造类和规划设计类人员分别为x人、y人.(1)用含x的代数式表示y;(2)若公司每月付给所招聘人员的工资为p元,要使本次招聘规划设计人员不少于机械制造人员的2倍,求p的取值范围.普通(元/间/天)三人间150双人间14010、一位水果销售商到果园购买荔枝和芒果,果园用两种规格不同的硬纸箱分别包装荔枝和芒果。(1)设每箱芒果的销售利润为x元,且每箱荔枝的销售利润比每箱芒果多7元,则每箱荔枝的销售利润为元(用含x的代数式表示)。(2)在(1)的条件下,该销售商第一次进货荔枝26箱,芒果18箱,售完后共获利534元,求每箱荔枝、芒果的销售利润各是多少元;(3)在(2)的条件下,销售商租用一辆车再次进货(已知这辆车完全装荔枝最多能装40箱,完全装芒果最多能装70箱),计划所购荔枝的箱数是芒果箱数的3倍少3箱,且售完后所获的利润不少于500元,销售商怎样进货获利最多?11、某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.(1)求商场经营该商品原来一天可获利润多少元?(2)设后来该商品每件降价x元,商场一天可获利润y元.①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?②求出y与x之间的函数关系式,并通过画该函数图像的草图,观察其图像的变化趋势,结合题意写出当x取何值时,商场获利润不少于2160元?