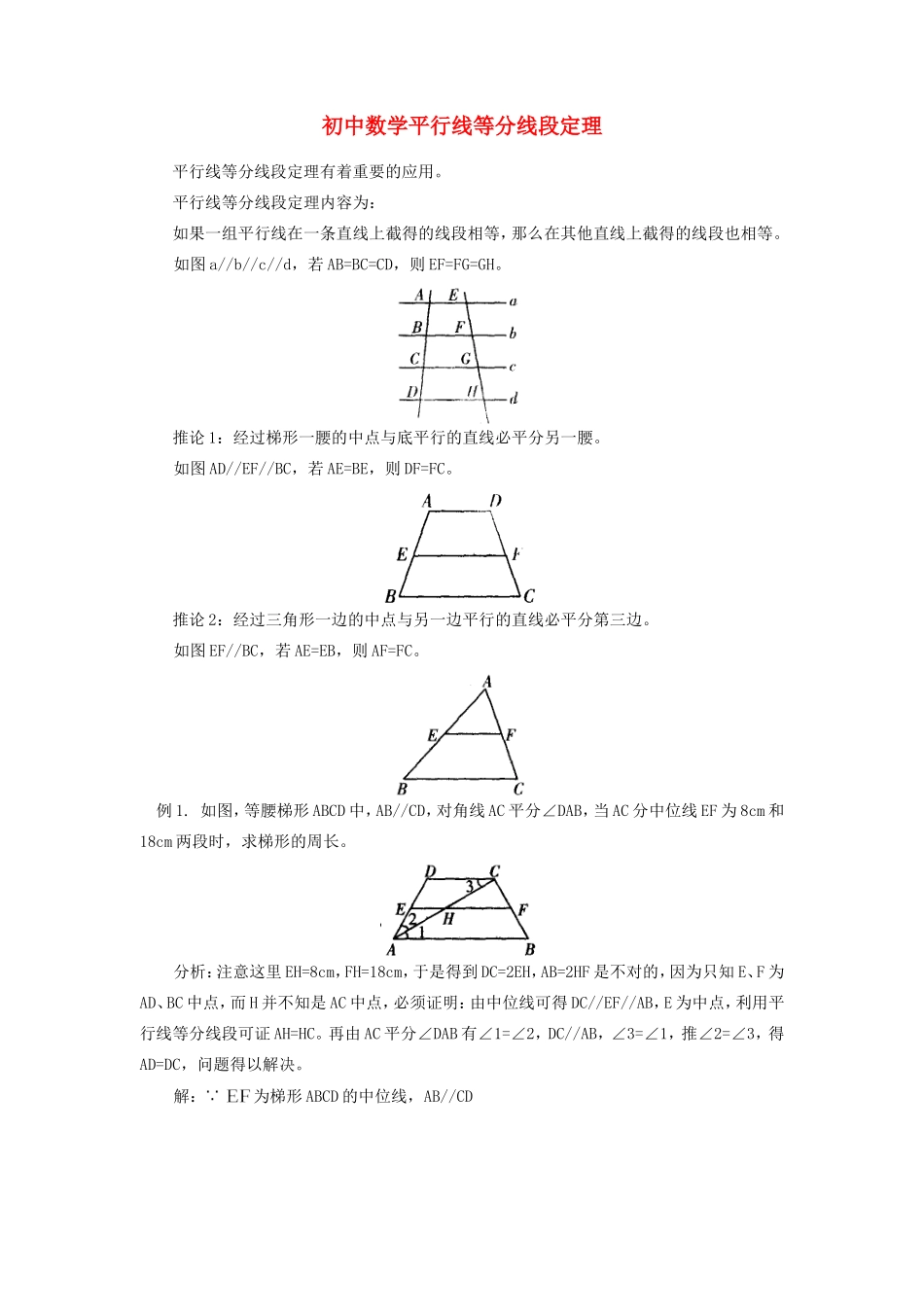
初中数学平行线等分线段定理平行线等分线段定理有着重要的应用。平行线等分线段定理内容为:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等。如图a//b//c//d,若AB=BC=CD,则EF=FG=GH。推论1:经过梯形一腰的中点与底平行的直线必平分另一腰。如图AD//EF//BC,若AE=BE,则DF=FC。推论2:经过三角形一边的中点与另一边平行的直线必平分第三边。如图EF//BC,若AE=EB,则AF=FC。例1.如图,等腰梯形ABCD中,AB//CD,对角线AC平分∠DAB,当AC分中位线EF为8cm和18cm两段时,求梯形的周长。分析:注意这里EH=8cm,FH=18cm,于是得到DC=2EH,AB=2HF是不对的,因为只知E、F为AD、BC中点,而H并不知是AC中点,必须证明:由中位线可得DC//EF//AB,E为中点,利用平行线等分线段可证AH=HC。再由AC平分∠DAB有∠1=∠2,DC//AB,∠3=∠1,推∠2=∠3,得AD=DC,问题得以解决。解:为梯形ABCD的中位线,AB//CD梯形ABCD的周长。点拨:该题关键在于证明H为AC的中点,才能使用三角形中位线定理,由角平分线、平行线可得等腰三角形,得到相等线段,从而代换出结果。例2.证明顺次连接对角线互相垂直的四边形各边中点,所得的四边形是矩形。已知:如图,在四边形ABCD中,于点O,E、F、G、H分别是边AB、BC、CD、DA的中点。求证:四边形EFGH是矩形。分析:由E、F、G,H为四边形ABCD各边的中点,联想到三角形中位线的性质,得到,可证四边形EFGH为平行四边形,又由,易证∠HEF=∠DOC=90°结论成立。证明:在中,E、H分别是AB、AD的中点。。(三角形中位线定理)同理,。,四边形EFGH是平行四边形。、F分别是AB、BC的中点,,于O,,又EH//BD,,四边形EFGH是矩形。点拨:顺次连结一个四边形各边的中点能否组成矩形、菱形、正方形,是使用三角形的中位线定理的典型题例,确定各边中点形成的四边形的形状,关键取决于已知四边形的对角线的关系:若已知四边形的对角线互相垂直,则所得的四边形是矩形。若已知四边形的对角线相等,则所得到的四边形是菱形。若已知四边形的对角线相等又互相垂直,则所得到的四边形是正方形。例3.如图,在梯形ABCD中,AD//BC(),E、F分别是对角线BD、AC的中点,求证:。分析:由于E、F是BD、AC的中点,EF既不是三角形的中位线,也不是梯形中位线。故连结AE并延长交BC于G,构造△AGC,证EF为△AGC的中位线,也就是证E为AG的中点。证明:连结AE并延长交BC于G,又F为AC中点,故EF是的中位线。。点拨:这里关键是构造三角形,使EF为其中位线。注意这里不能直接应用三角形中位线(或梯形中位线)的性质来解题,以致错误。例4.如图所示,中,,AD平分∠BAC,,点E是BC的中点,求证:①,②。分析:由条件E是BC的中点,结论DE∥AB,联想到三角形的中位线定理。于是延长CD交AB于F,证明D是CF的中点,这易证明。结论获解决。证明:①延长CD交AB于F。又BE=EC,的中位线,(三角形的中位线定理)。②由(1)知DE为的中位线,AC=AF,。点拨:在三角形中,若有一边的中点或倍分关系时,常作出三角形的中位线,或证明为中位线,利用三角形的中位线定理加以解决。年级初中学科数学版本期数内容标题平行线等分线段定理分类索引号G.622.46分类索引描述辅导与自学主题词平行线等分线段定理栏目名称专题辅导供稿老师审稿老师录入常丽霞一校林卉二校审核