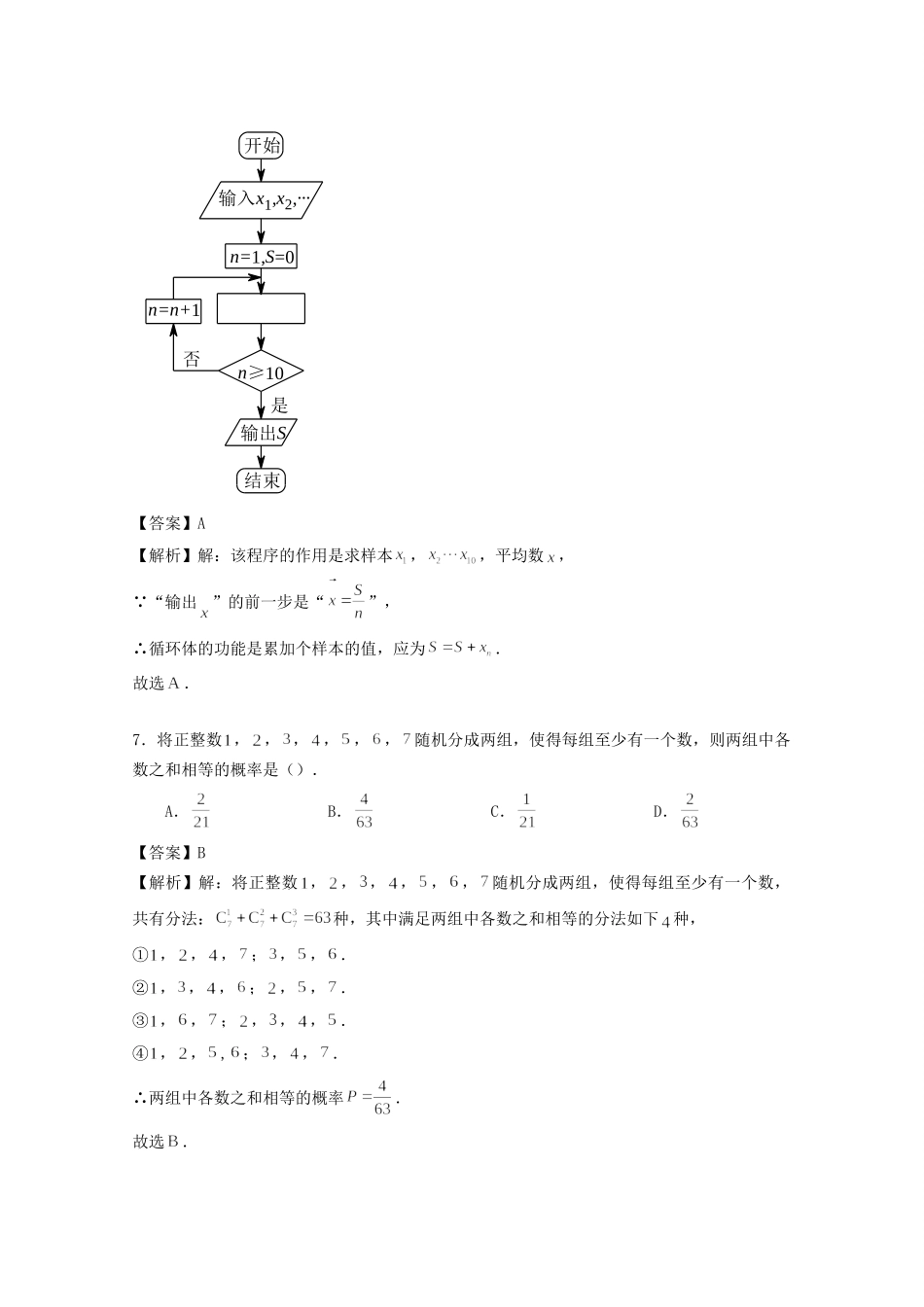
北京市西城八中2016-2017学年高一数学下学期期末考试试题(含解析)考试时间120分钟,满分150分一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,将答案填在括号里)1.已知,,则是的()条件.A.充分不必要B.必要不充分C.充要D.既不充分也不必要【答案】A【解析】解: ,可得,设集合为,又 ,可得,设集合为,则,可得是的充分不必要条件.2.下列函数中,在区间上为增函数的是().A.B.C.D.【答案】A【解析】解:项、在上为增函数,符合题目要求.故选.3.将函数的图像沿轴向左平移个单位,得到一个偶函数的图像,则的一个可能取值为().A.B.C.D.【答案】C【解析】解: 左移个单位,函数变为, 是偶函数,取为,则,∴,∴,取,得,即一个可能取值为.故选.4.在二项式的展开式中,含的项的系数是().A.B.C.D.【答案】C【解析】解:的展开项,令,可得,∴.故选.5.将名学生分到两个班级,每班至少人,不同的方法有()种.A.B.C.D.【答案】C【解析】解:名学生中有名学生分在一个班的种数为,有名学生分在一个班有种结果,∴种,共有种结果.故选.6.右图是求样本,,,平均数的程序框图,图中空白框中应填入的内容的().A.B.C.D.n=n+1n≥10n=1,S=0输入x1,x2,∙∙∙输出S是否开始结束【答案】A【解析】解:该程序的作用是求样本,,平均数, “输出”的前一步是“”,∴循环体的功能是累加个样本的值,应为.故选.7.将正整数,,,,,,随机分成两组,使得每组至少有一个数,则两组中各数之和相等的概率是().A.B.C.D.【答案】B【解析】解:将正整数,,,,,,随机分成两组,使得每组至少有一个数,共有分法:种,其中满足两组中各数之和相等的分法如下种,①,,,;,,.②,,,;,,.③,,;,,,.④,,,;,,.∴两组中各数之和相等的概率.故选.8.已知集合,其中,且,则中所有元素之和是().A.B.C.D.【答案】C【解析】解:根据集合的形式,可以把,,,看做四位二进制数,四位二进制共可以表示至, ,∴可表示至的数字,由等差数列求和可得.故选.二、填空题(本大题共6小题,每小题5分,共30分.把答案填在题中横线上)9.在中,若,,,__________.【答案】【解析】解: ,,,,由正弦定理,∴.10.在等比数列中,若,,则__________.【答案】【解析】解:设等比数列中公比为, ,∴,∴.11.已知,均为单位向量,它们的夹角为,那么__________.【答案】【解析】解: .12.设函数,对任意实数,关于的方程总有实数根,则的取值范围是__________.【答案】【解析】解: 对任意实数,关于的方程总有实数根,即对任意实数函数的图像与直线总有交点,奇函数的值域为,在同一坐标系中画出与的图像,1yx由图可得,当时,函数的值域为,∴.13.若,其中,则实数__________.__________.【答案】;【解析】解:由题意的展开式的通项为,令得, ,∴,解得,在展开式中令得,即.14.设为不等式组所表示的平面区域,为不等式组所表示的平面区域,其中,在内随机取一点,记点在内的概率为.()若,则__________.()的最大值是__________.【答案】;【解析】解:由题意可得,当时,如图,,4yx44如图,当取得最大值时,最大,最大值为.xy4三、解答题(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤)15.(本小题满分分)设的内角,,所对的边分别为,,,且,.()若,求角的度数.()求面积的最大值.【答案】().().【解析】() ,,由正弦定理,∴,∴.() ,∴, ,∴,∴,当且仅当时,等号成立,,∴的面积的最大值为.16.(本小题满分分)已知函数.()求函数的定义域及其单调减区间.()求函数的值域.【答案】()定义域为,单调递减区间为.().【解析】解:() , ,即单调递减区间为, 中,,定义域为.() ,∴.17.(本小题满分分)一名学生骑自行车上学,从他家到学校的途中有个交通岗,假设他在各个交通岗遇到红灯的事件是相互独立的,并且概率都是.求:()这...