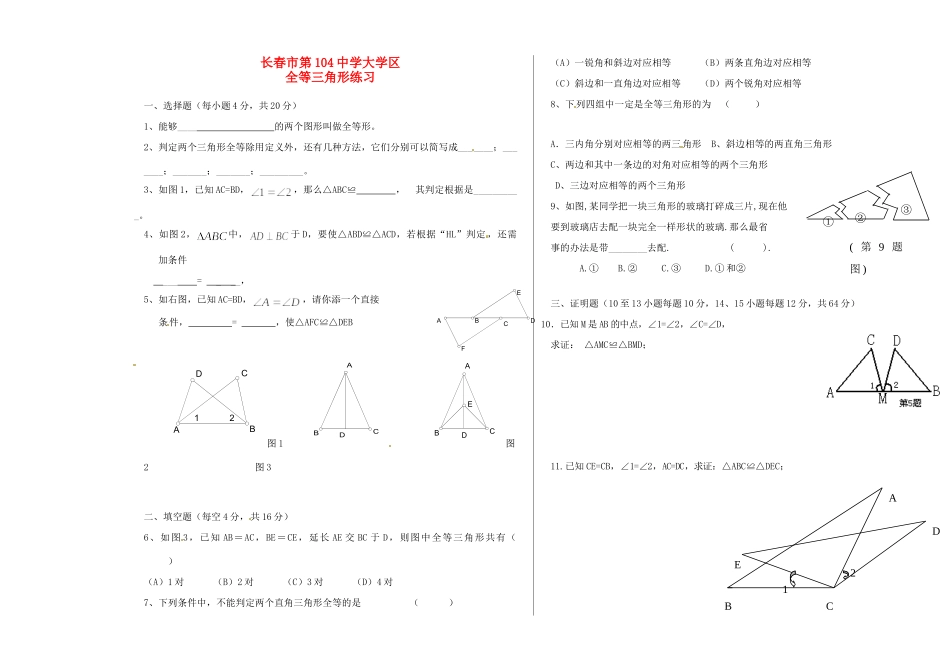
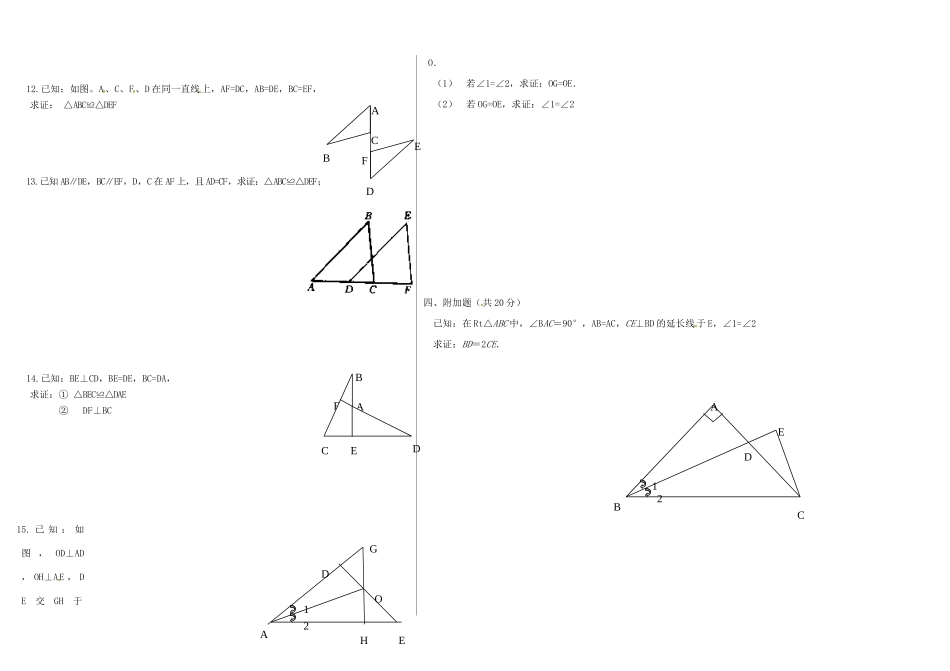
长春市第104中学大学区全等三角形练习一、选择题(每小题4分,共20分)1、能够____的两个图形叫做全等形。2、判定两个三角形全等除用定义外,还有几种方法,它们分别可以简写成_______;_______;_______;_______;_________。3、如图1,已知AC=BD,,那么△ABC≌,其判定根据是__________。4、如图2,中,于D,要使△ABD≌△ACD,若根据“HL”判定,还需加条件___=___,5、如右图,已知AC=BD,,请你添一个直接条件,=,使△AFC≌△DEB图1图2图3二、填空题(每空4分,共16分)6、如图3,已知AB=AC,BE=CE,延长AE交BC于D,则图中全等三角形共有()(A)1对(B)2对(C)3对(D)4对7、下列条件中,不能判定两个直角三角形全等的是()(A)一锐角和斜边对应相等(B)两条直角边对应相等(C)斜边和一直角边对应相等(D)两个锐角对应相等8、下列四组中一定是全等三角形的为()A.三内角分别对应相等的两三角形B、斜边相等的两直角三角形C、两边和其中一条边的对角对应相等的两个三角形D、三边对应相等的两个三角形9、如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带________去配.().A.①B.②C.③D.①和②三、证明题(10至13小题每题10分,14、15小题每题12分,共64分)10.已知M是AB的中点,∠1=∠2,∠C=∠D,求证:△AMC≌△BMD;11.已知CE=CB,∠1=∠2,AC=DC,求证:△ABC≌△DEC;ADEBFCBCADBCAEDABCD12BECDA12(第9题图)③①②12.已知:如图。A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF,求证:△ABC≌△DEF13.已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,求证:△ABC≌△DEF;14.已知:BE⊥CD,BE=DE,BC=DA,求证:①△BEC≌△DAE②DF⊥BC15.已知:如图,OD⊥AD,OH⊥AE,DE交GH于O.(1)若∠1=∠2,求证:OG=OE.(2)若OG=OE,求证:∠1=∠2四、附加题(共20分)已知:在Rt△ABC中,∠BAC=90°,AB=AC,CE⊥BD的延长线于E,∠1=∠2求证:BD=2CE.BCDEFABCDEA21BCDEFAA1EOD2GH