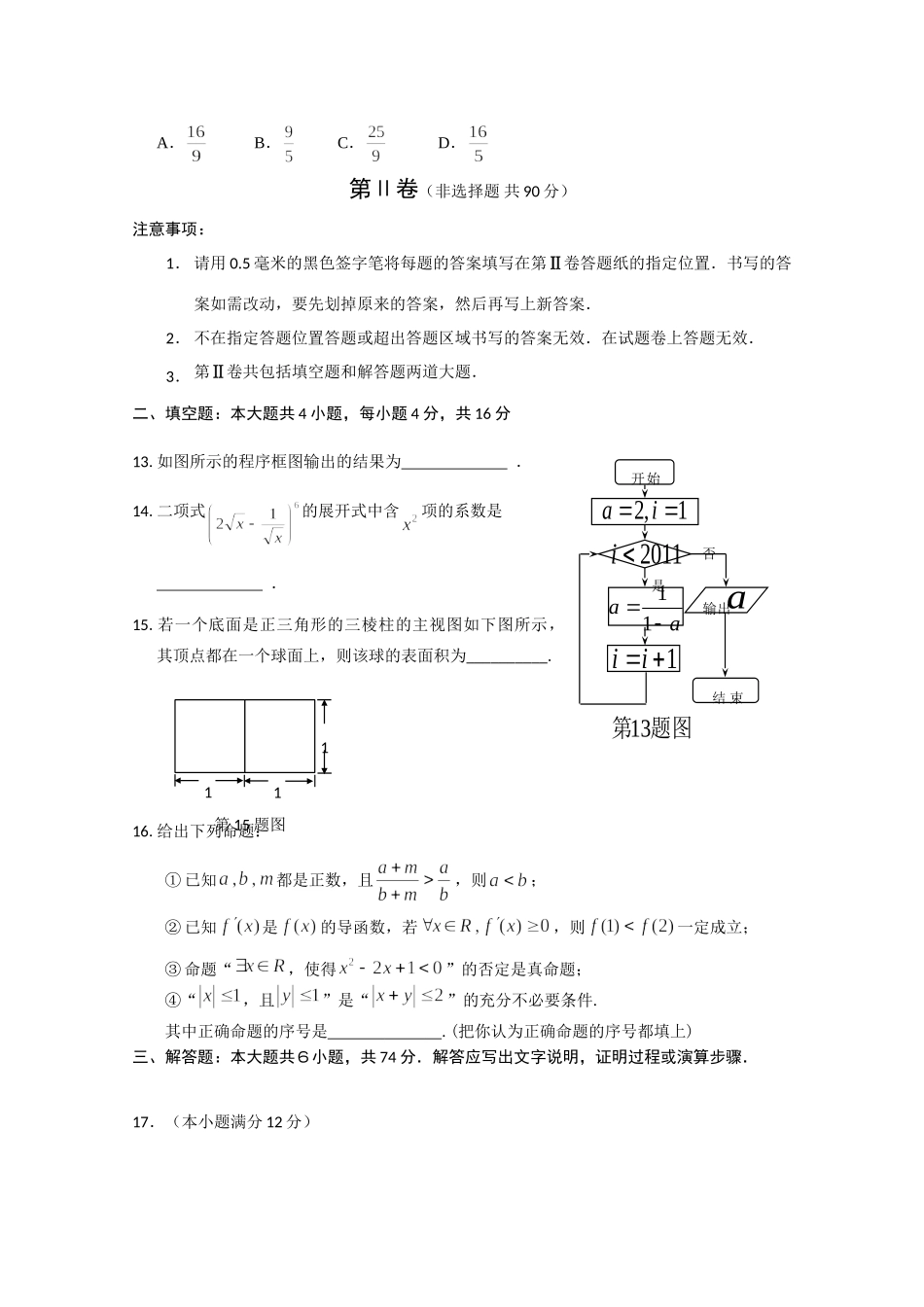
绝密★启用前2011年威海市高考模拟考试理科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共6页.考试时间120分钟.满分150分.答题前,考生务必用0.5毫米的黑色签字笔将自己的姓名、座号、考号填写在第Ⅰ卷答题卡和第Ⅱ卷答题纸规定的位置.参考公式:样本数据的标准差其中为样本平均数球的面积公式第Ⅰ卷(选择题共60分)注意事项:1.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.2.第Ⅰ卷只有选择题一道大题.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数(是虚数单位)的虚部是A.B.C.D.2.已知是实数集,,则A.B.C.D.3.现有个数,其平均数是,且这个数的平方和是,那么这个数组的标准差是A.B.C.D.4.设为等比数列{}na的前项和,,则A.B.C.D.155.已知函数,若存在,使得恒成立,则的值是A.B.C.D.6.已知、表示直线,,,表示平面,给出下列四个命题,其中真命题为(1)则,,,mnnm(2)mnnm则,,,(3)则∥(4)则,,,nmnmA.(1)、(2)B.(3)、(4)C.(2)、(3)D.(2)、(4)7.若等边的边长为,平面内一点满足,则A.B.C.D.8.已知三角形的三边长成公差为的等差数列,且最大角的正弦值为,则这个三角形的周长是A.B.C.D.9.过直线上一点引圆的切线,则切线长的最小值为A.B.C.D.10.已知函数的导函数为,且满足,则A.B.C.D.11.已知函数.若都是区间内的数,则使成立的概率是A.B.C.D.12.已知双曲线的标准方程为,为其右焦点,是实轴的两端点,设为双曲线上不同于的任意一点,直线与直线分别交于两点,若,则的值为否开始输出结束是2011i1,2iaaa11题图第131iiaA.B.C.D.第Ⅱ卷(非选择题共90分)注意事项:1.请用0.5毫米的黑色签字笔将每题的答案填写在第Ⅱ卷答题纸的指定位置.书写的答案如需改动,要先划掉原来的答案,然后再写上新答案.2.不在指定答题位置答题或超出答题区域书写的答案无效.在试题卷上答题无效.3.第Ⅱ卷共包括填空题和解答题两道大题.二、填空题:本大题共4小题,每小题4分,共16分13.如图所示的程序框图输出的结果为.14.二项式的展开式中含项的系数是.15.若一个底面是正三角形的三棱柱的主视图如下图所示,其顶点都在一个球面上,则该球的表面积为__________.16.给出下列命题:①已知都是正数,且,则;②已知是的导函数,若,则一定成立;③命题“,使得”的否定是真命题;④“,且”是“”的充分不必要条件.其中正确命题的序号是.(把你认为正确命题的序号都填上)三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)第15题图111已知向量共线,且有函数.(Ⅰ)若,求的值;(Ⅱ)在中,角的对边分别是,且满足,求函数的取值范围.18.(本小题满分12分)已知等差数列的前项和为,公差成等比数列.(Ⅰ)求数列的通项公式;(Ⅱ)设是首项为1,公比为3的等比数列,求数列nb的前n项和nT.19.(本小题满分12分)如图,在正三棱柱中,,是上的动点,且,是的中点.(Ⅰ)若,求证:;(Ⅱ)若直线与平面所成角的大小为,试求的值.ACBA11C11B11MNBxyAOPQ20.(本小题满分12分)四枚不同的金属纪念币,投掷时,两枚正面向上的概率均为,另两枚(质地不均匀)正面向上的概率均为().将这四枚纪念币同时投掷一次,设ξ表示出现正面向上的枚数.(Ⅰ)求ξ的分布列(用表示);(Ⅱ)若有一枚正面向上对应的概率最大,求的取值范围.21.(本小题满分12分)已知函数在点的切线方程为.(Ⅰ)求函数的解析式;(Ⅱ)设,求证:在上恒成立;(Ⅲ)已知,求证:.22.(本小题满分14分)已知椭圆的中心在原点,焦点在轴上,离心率等于,它的一个顶点恰好是抛物线的焦点.(Ⅰ)求椭圆的方程;(Ⅱ)是椭圆上两点,、是椭圆位于直线两侧的两动点,(i)若直线的斜率为求四边形面积的最大值;(ii)当、运动时,满足,试问直线的斜率...