九年级数学上册 期末考试模拟题1 北师大版试卷VIP免费

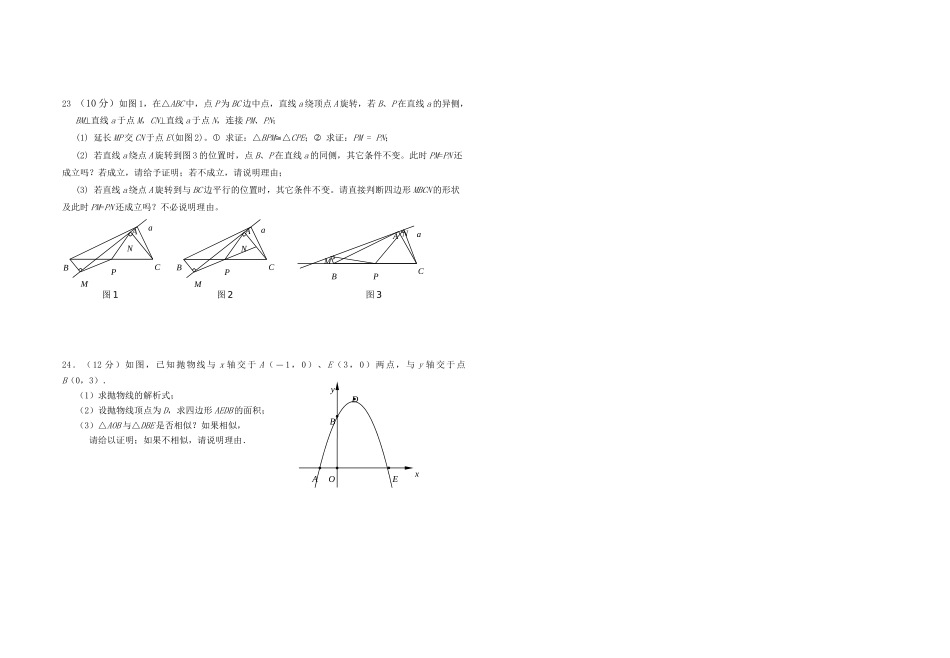
九年级期末1一、选择题（每小题3分，共27分）1、一元二次方程xx32的根为（）A、3xB、01x，32xC、3xD、31x，02x2、菱形具有而平行四边形不一定具有的性质是（）A、对角相等B、对边相等C、邻边相等D、对边平行3.既是轴对称图形，又是中心对称图形的是【】A.矩形B.平行四边形C.正三角形D.等腰梯形4.已知正比例函数)0(11kxky与反比例函数)0(22kxky的图象有一个交点的坐标为(-2,-1),则它们的另一个交点的坐标是【】A.(2,1)B.(-2,-1)C.(-2,1)D.(2,-1)5.在一个四边形ABCD中,依次连接各边的中点得到的四边形是菱形,则对角线AC与BD需要满足条件是【】A.垂直B.相等C.垂直且相等D.不再需要条件6.已知点A(-2,y1),(-1,y2),(3,y3)都在反比例函数xy4的图象上,则【】A.y1＜y2＜y3B.y3＜y2＜y1C.y3＜y1＜y2D.y2＜y1＜y37.下列说法中，错误的是【】Ａ.一组对边平行且相等的四边形是平行四边形Ｂ.两条对角线互相垂直且平分的四边形是菱形Ｃ.四个角都相等的四边形是矩形Ｄ.邻边都相等的四边形是正方形8、若二次函数)2(2mmxmxy的图象经过原点，则m的值必为()A．0或2B．0C．2D．无法确定9、已知二次函数cbxaxy2的图象如图，下列结论：①0cba;②0cba;③0abc;④ab2；⑤，△0正确的个数是()A4个B3个C2个D1个二、填空题（每题3分，共18分）10、把抛物线23xy向上平移2个单位,再向右平移3个单位，则所得的抛物线是___________11、菱形的两条对角线长分别为6和8，则此菱形的面积为___________。12、在Rt△ABC中，∠C=900，sinA=1213，则sinB=.13、如果反比例函数xky3的图象过点（2，-3），那么k=。14、为了估计不透明的袋子里装有多少白球，先从袋中摸出10个球都做上标记，然后放回袋中去，充分摇匀后再摸出10个球，发现其中有一个球有标记，那么你估计袋中大约有______个白球15、已知某工厂计划经过两年的时间，把某种产品从现在的年产量100万台提高到121万台，那么每年平均增长的百分数是，按此年平均增长率，预计到第4年该工厂的年产量应为台.三、解答题16、（6分）解方程：22)2(2323xxxyxO-117、（6分）画出图中三棱柱的三视图。18、（8分）如图，甲转盘被分成3个面积相等的扇形，乙转盘被分成4个面积相等的扇形，每一个扇形都标有相应的数字．同时转动两个转盘，当转盘停止后，设甲转盘中指针所指区域内的数字为x，乙转盘中指针所指区域内的数字为y（当指针指在边界线上时，重转一次，直到指针指向一个区域为止）.（1）请你用画树状图或列表格的方法，求出点,xy落在第二象限内的概率；（2）直接写出点,xy落在函数1yx图象上的概率.19、（9分）如图，点Ａ是双曲线xky与直线y=-x-(k+1)在第二象限内的交点，ＡＢ⊥x轴于B，且Ｓ△ABO＝23.（１）求这两个函数的解析式；（２）求直线与双曲线的两个交点Ａ、Ｃ的坐标和△AOC的面积.20.（6分）如图，菱形ABCD的对角线AC与BD相交于点O，点E、F分别为边AB、AD的中点，连接EF、OE、OF。求证：四边形AEOF是菱形。21.（9分）星期天，小强去水库大坝游玩，他站在大坝上的A处看到一棵大树的影子刚好落在坝底的B处（点A与大树及其影子在同一平面内），此时太阳光与地面成600角.在A处测得树顶D的俯角为150.如图所示，已知AB与地面的夹角为600，AB为8米.请你帮助小强计算一下这颗大树的高度？(结果精确到1米.参考数据2≈1.43≈1.7)22、（9分）某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价一元，日销售量将减少20千克。（1）现要保证每天盈利6000元，同时又要让顾客得到实惠，那么每千克应涨价多少元？（2）若该商场单纯从经济角度看，那么每千克应涨价多少元，能使商场获利最多。ABCDEFO23（10分）如图1，在△ABC中，点P为BC边中点，直线a绕顶点A旋转，若B、P在直线a的异侧，BM直线a于点M，CN直线a于点N，连接PM、PN；(1)延长MP交CN于点E(如图2)。求证：△BPM△CPE；求证：PM=PN；(2)若直线a绕点A旋转到图3的位置时，点B、P在直线a的同侧，其它条件不变。此时PM=PN还成立吗？若成立，...