《露在外面的面》教学设计与反思VIP专享VIP免费

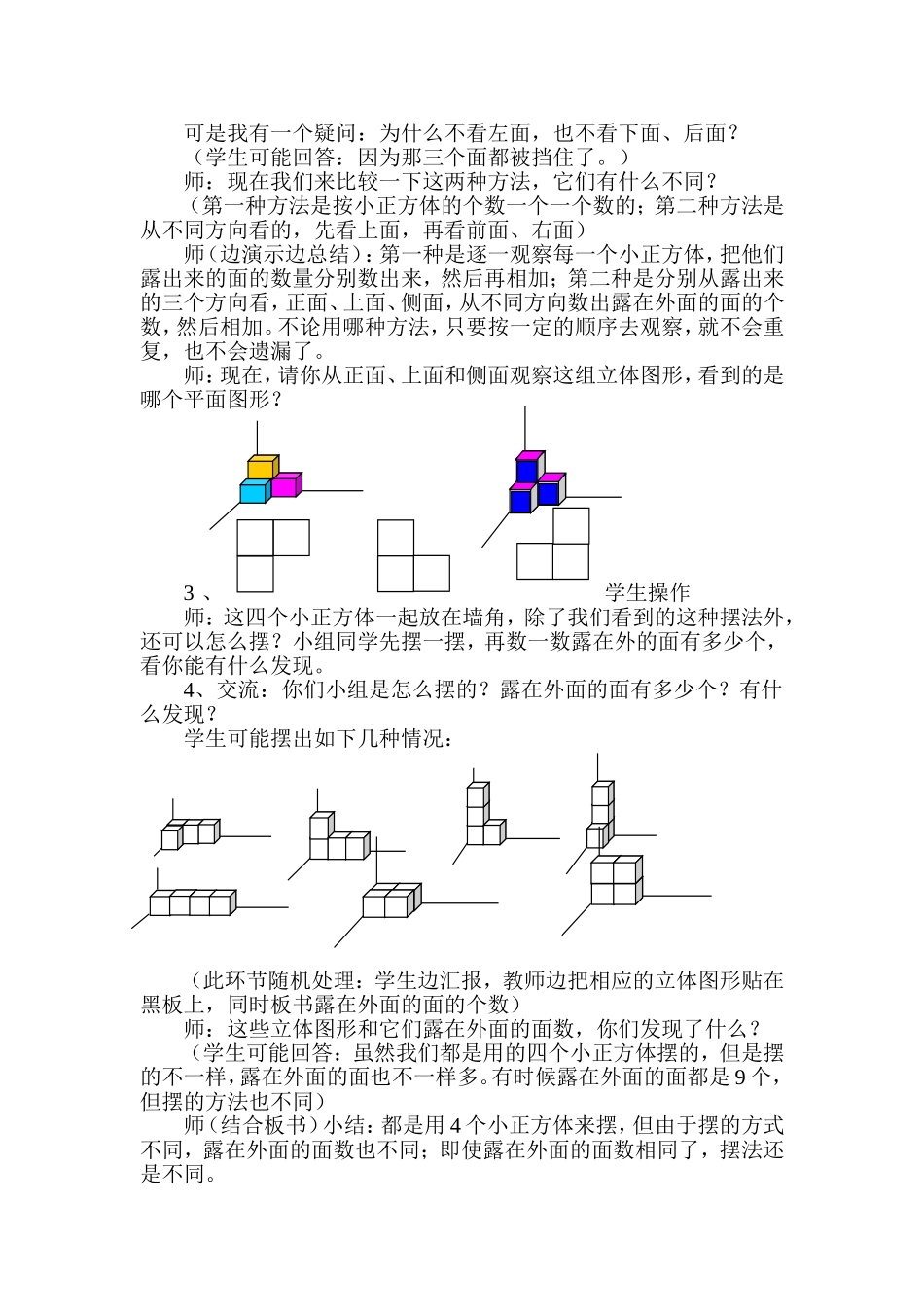
《露在外面的面》教学设计与反思城北中心校刘伟【教学内容】露在外面的面【教学目标】1、能够认识长方体和正方体，具有初步的立体空间想象能力。2、结合具体的多个长方体和正方体的堆放情景，经历探究多个长方体和正方体堆放时露在外面表面积的过程，能够准确的计算出多个长方体和正方体堆放时露在外面的表面积。3、使学生感受到长方体和正方体的表面积与生活的密切联系，培养学习数学的良好兴趣。【教学重难点】能够准确计算出多个正方体堆放时露在外面表面积。【教学准备】多媒体课件，每组8个完全相同的小正方体，记录卡，纸板等。【教学过程】一、谈话引入，运用方法。1、师：请看大屏幕，这是一组立体图形，看谁能最先看出：它是由几个小正方体组成的？（有8个小正方体）师：能说一说你是怎么看的吗？2、师：看来仅有观察还是不够的，还要在观察基础上加入合理的推想，把你视线所及看不到的在脑海中想到，才会得出正确结论。这节课，我们就继续用观察和推想这两种方法来探索《露在外面的面》（板书课题）二、操作体验，探索新知。1、师（请看大屏幕）：一个小正方体放在墙角，有几个面露在外面？哪几个？2、继续看大屏幕，这有几个小正方体？（学生可能回答：有4个小正方体）师：它有几个面露在外面？你怎么想的？（学生可能回答：露在外面的有9个面。上面的小正方体有3个面露在外面，前边的小正方体也露出3个面，右边的小正方体也一样，3+3+3=9，所以一共有9个面）师追问：不是有四个小正方体吗？你怎么只数了三个？（学生可能回答：有一个小正方体的面全被挡住了，一个也没露出来，就不用看了）师生一起按照上面、左面和右面的顺序数露在外面的面。师：他是这么数的，谁和他想法不一样？（学生可能回答：我先看正面，一共有三个小正方形；再看上面，也有三个小正方形；再看右面，也有三个小正方形。3+3+3=9，所以一共有9个面露在外面）师：谁听清了，他是怎么数的？（生重复方法）师生共同按这一方法数。可是我有一个疑问：为什么不看左面，也不看下面、后面？（学生可能回答：因为那三个面都被挡住了。）师：现在我们来比较一下这两种方法，它们有什么不同？（第一种方法是按小正方体的个数一个一个数的；第二种方法是从不同方向看的，先看上面，再看前面、右面）师（边演示边总结）：第一种是逐一观察每一个小正方体，把他们露出来的面的数量分别数出来，然后再相加；第二种是分别从露出来的三个方向看，正面、上面、侧面，从不同方向数出露在外面的面的个数，然后相加。不论用哪种方法，只要按一定的顺序去观察，就不会重复，也不会遗漏了。师：现在，请你从正面、上面和侧面观察这组立体图形，看到的是哪个平面图形？3、学生操作师：这四个小正方体一起放在墙角，除了我们看到的这种摆法外，还可以怎么摆？小组同学先摆一摆，再数一数露在外的面有多少个，看你能有什么发现。4、交流：你们小组是怎么摆的？露在外面的面有多少个？有什么发现？学生可能摆出如下几种情况：（此环节随机处理：学生边汇报，教师边把相应的立体图形贴在黑板上，同时板书露在外面的面的个数）师：这些立体图形和它们露在外面的面数，你们发现了什么？（学生可能回答：虽然我们都是用的四个小正方体摆的，但是摆的不一样，露在外面的面也不一样多。有时候露在外面的面都是9个，但摆的方法也不同）师（结合板书）小结：都是用4个小正方体来摆，但由于摆的方式不同，露在外面的面数也不同；即使露在外面的面数相同了，摆法还是不同。现在我们算一算，不同摆法中，露在外面的面的面积是多少，已知正方体棱长10厘米，从黑板上的立体图形中选一个你自己喜欢的摆法，快算一算吧。学生汇报5、师：上课前，我们观察过这组立体图形，现在请你再看一看，它露在外面的小正方形有多少个？（一共有26个）师：你是怎么看的？（学生可能回答：先看前面，一共有6个，后面和前面一样多，也有6个；右面有5个，左面也有5个；上面有4个，所以就有26个小正方形露在外面）师：他能有序地进行观察，前、后、左、右、上，还发现了相对的面露出来的小正方形的个数是一样多的：左右一样多，前后一样多。可真了不起！师：...