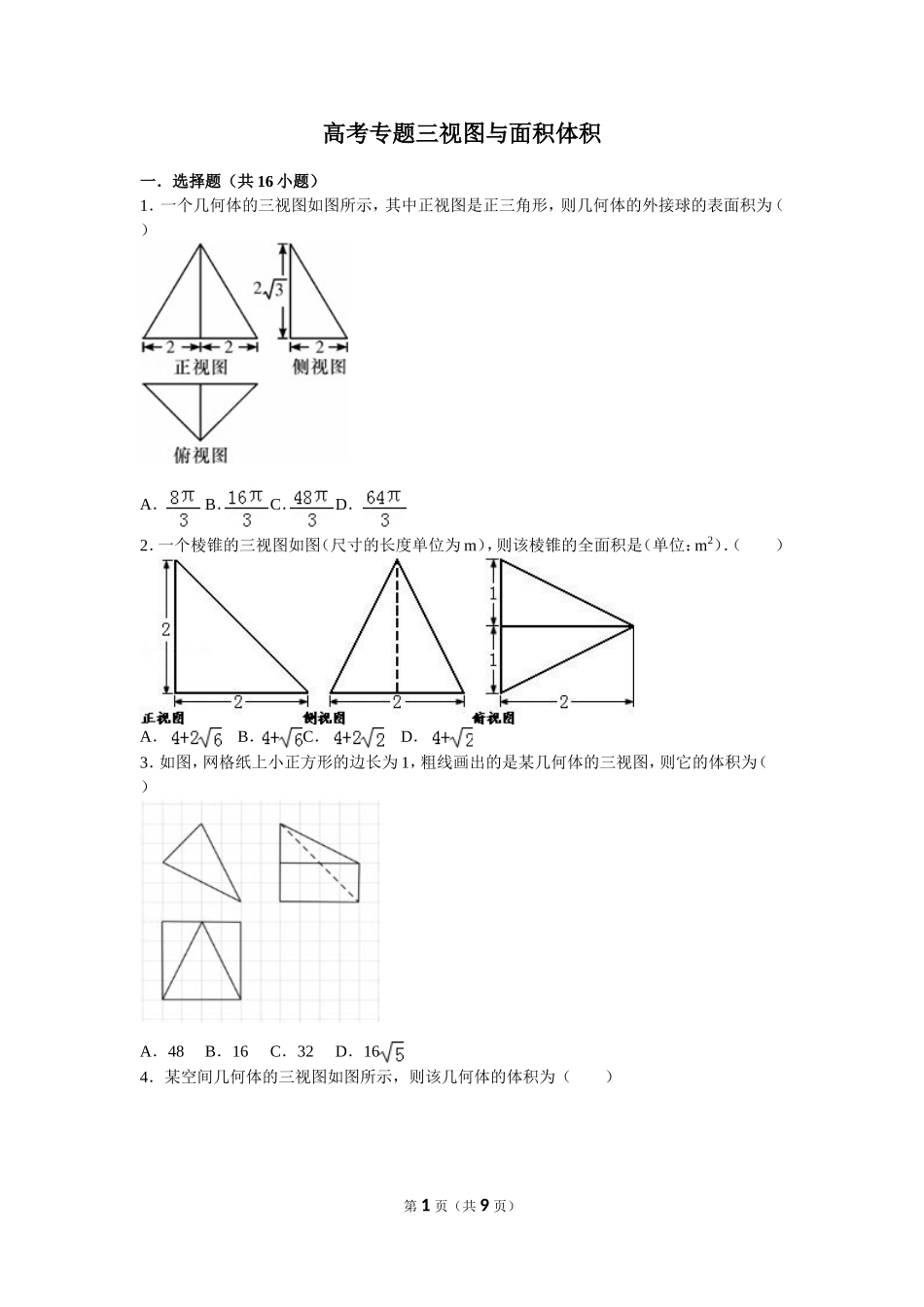
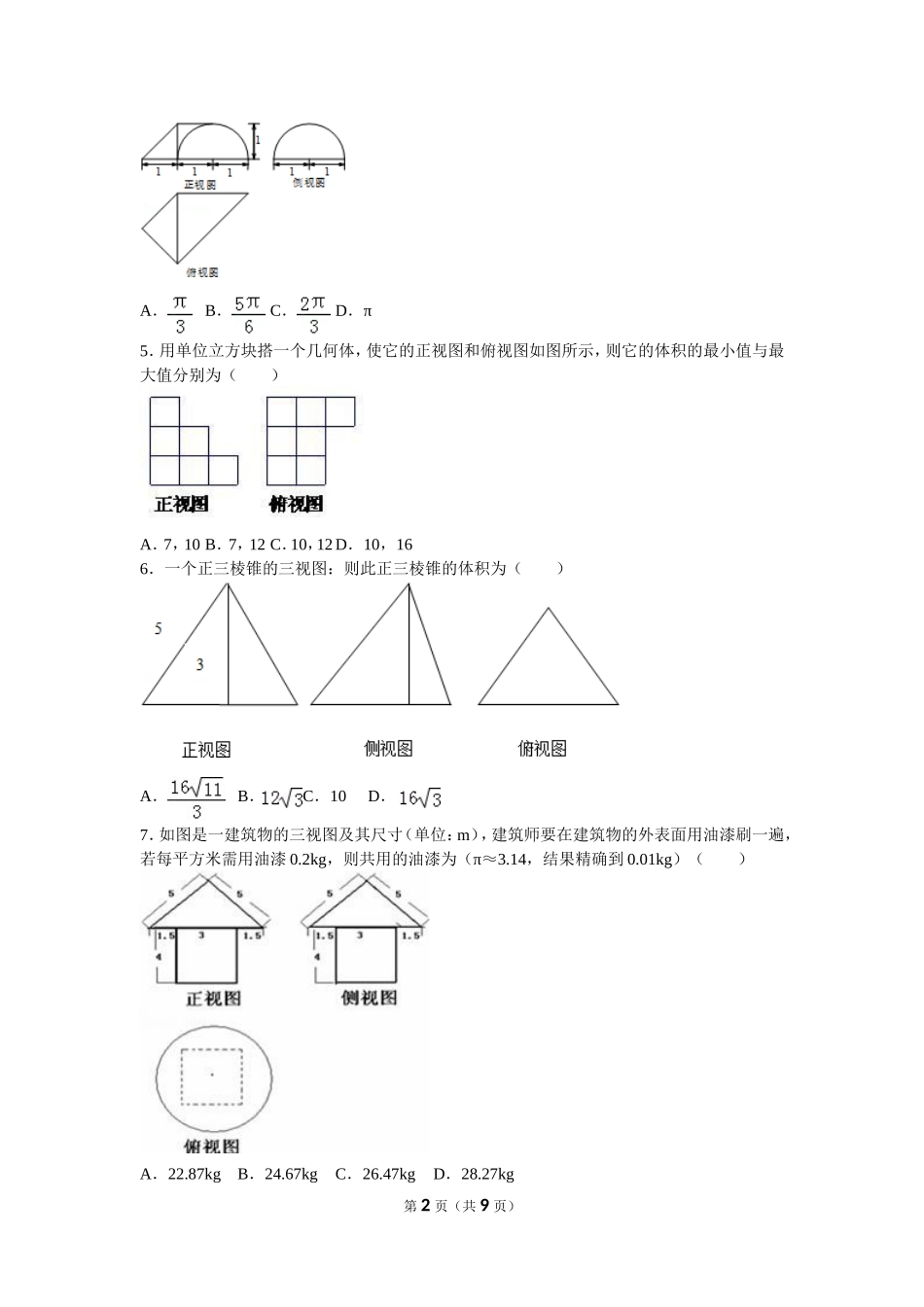
高考专题三视图与面积体积一.选择题(共16小题)1.一个几何体的三视图如图所示,其中正视图是正三角形,则几何体的外接球的表面积为()A.B.C.D.2.一个棱锥的三视图如图(尺寸的长度单位为m),则该棱锥的全面积是(单位:m2).()A.B.C.D.3.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则它的体积为()A.48B.16C.32D.164.某空间几何体的三视图如图所示,则该几何体的体积为()第1页(共9页)A.B.C.D.π5.用单位立方块搭一个几何体,使它的正视图和俯视图如图所示,则它的体积的最小值与最大值分别为()A.7,10B.7,12C.10,12D.10,166.一个正三棱锥的三视图:则此正三棱锥的体积为()A.B.C.10D.7.如图是一建筑物的三视图及其尺寸(单位:m),建筑师要在建筑物的外表面用油漆刷一遍,若每平方米需用油漆0.2kg,则共用的油漆为(π≈3.14,结果精确到0.01kg)()A.22.87kgB.24.67kgC.26.47kgD.28.27kg第2页(共9页)8.一个棱锥的三视图如图,则该棱锥的全面积(单位:cm2)为()A.48+12B.48+24C.36+12D.36+249.某几何体的三视图如图所示,它的表面积为()A.B.C.D.π10.在如图所示的空间直角坐标系Oxyz﹣中,一个四面体的顶点坐标分别为(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出的编号为①,②,③,④的四个图,则该四面体的正视图和俯视图分别为()A.①和②B.③和①C.④和③D.④和②11.如图,已知三棱锥的底面是直角三角形,直角边长分别为3和4,过直角顶点的侧棱长为4,且垂直于底面,该三棱锥的正视图是()第3页(共9页)A.B.C.D.12.已知圆锥的母线长与底面半径长之比为3:1,一个正方体有四个顶点在圆锥的底面内,另外的四个顶点在圆锥的侧面上(如图),则圆锥与正方体的表面积之比为()A.π:1B.3π:1C.3π:2D.3π:413.棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,则图中三角形(正四面体的截面)的面积是()A.B.C.D.14.已知某几何体的三视图如图所示,过该几何体最短两条棱的中点作平面α,使得α平分该几何体的体积,则可以作此种平面α()A.恰好1个B.恰好2个C.至多3个D.至少4个15.一条长为2的线段,它的三个视图分别是长为的三条线段,则ab的最大值为()第4页(共9页)A.B.C.D.316.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的()A.外接球的半径为B.表面积为C.体积为D.外接球的表面积为4π二.填空题(共14小题)17.一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在同一个球面上,则这个球的表面积是.18.已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的外接球体积为.19.一个几何体三视图如图,则此几何体体积为.20.某几何体的三视图如图所示,则这个几何体的体积是.第5页(共9页)21.设某几何体的三视图如图(尺寸的长度单位为:m),若该几何体的各个顶点都在同一球面上,则此球的表面积等于m2(答案用含有π的式子表示)22.一个三棱锥的三视图如图所示,其正视图、侧视图、俯视图的面积分别为4,6,12,则这个几何体的体积为.23.一个几何体的三视图如图所示,主视图、左视图、俯视图均为腰长为1的等腰直角三角形,则其外接球的表面积为.24.设某几何体的三视图如图(尺寸的长度单位为m)则该几何体的体积为m3.第6页(共9页)25.如图为一个几何体的三视图,AB=BC=1,BB1=2,则此几何体的表面积为.26.如图为一个棱长为2cm的正方体被过其中三个顶点的平面削去一个角后余下的几何体,试画出它的正视图.27.如图,正四面体ABCD的棱长为1,平面α过棱AB,且CD∥α,则正四面体上的所有点在平面α内的射影构成的图形面积是.28.如图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是.(要求:把可能的图的序号都填上)第7页(共9页)29.一个水平放置的△ABC用斜二测画法画出的直观图是如图273﹣﹣所示的边长为1的正△A'B'C',则在真实图形中AB边...