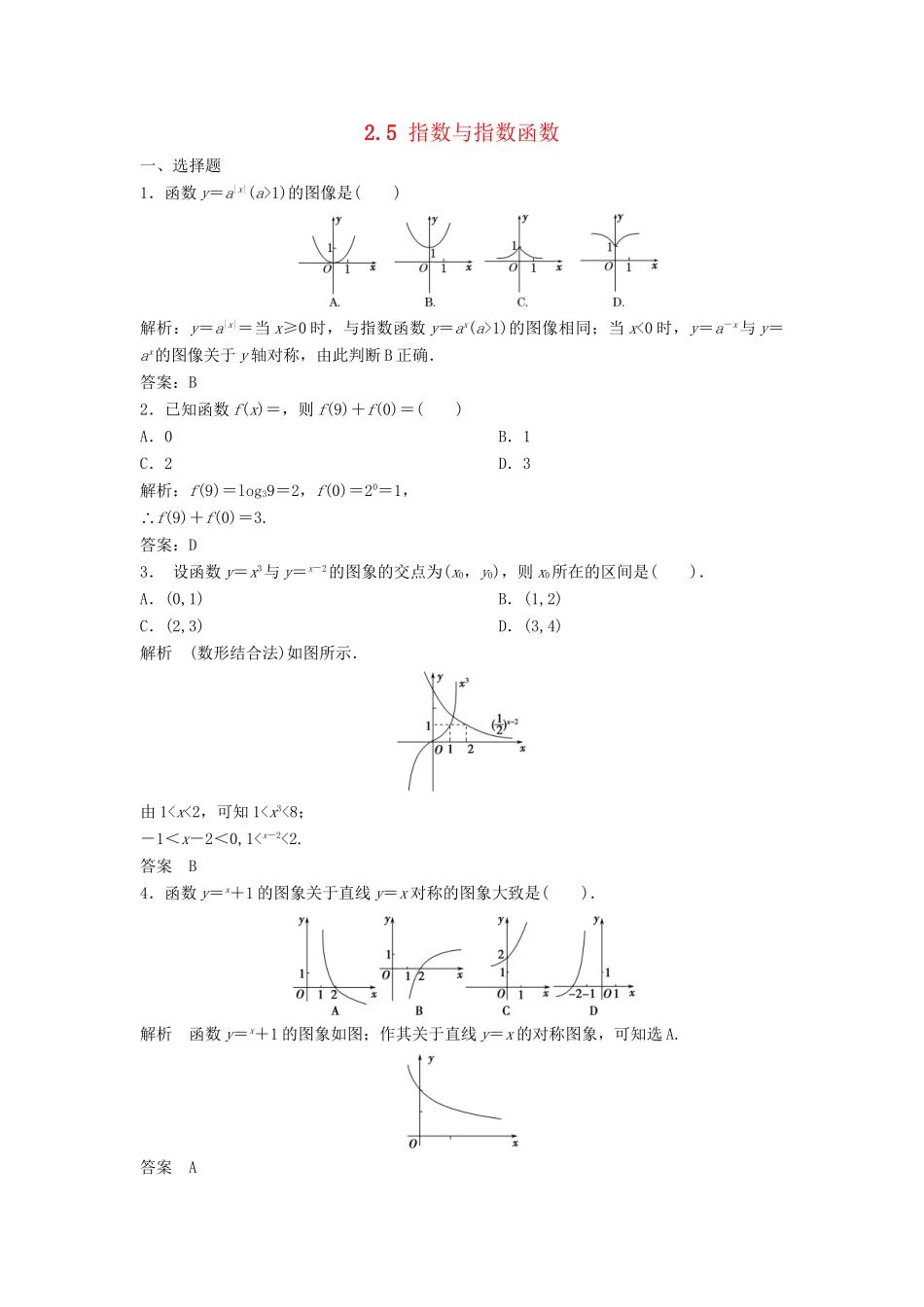
2.5指数与指数函数一、选择题1.函数y=a|x|(a>1)的图像是()解析:y=a|x|=当x≥0时,与指数函数y=ax(a>1)的图像相同;当x<0时,y=a-x与y=ax的图像关于y轴对称,由此判断B正确.答案:B2.已知函数f(x)=,则f(9)+f(0)=()A.0B.1C.2D.3解析:f(9)=log39=2,f(0)=20=1,∴f(9)+f(0)=3.答案:D3.设函数y=x3与y=x-2的图象的交点为(x0,y0),则x0所在的区间是().A.(0,1)B.(1,2)C.(2,3)D.(3,4)解析(数形结合法)如图所示.由1
1,b>0,且ab+a-b=2,则ab-a-b的值为()A.B.2或-2C.-2D.2解析:(ab+a-b)2=8⇒a2b+a-2b=6,∴(ab-a-b)2=a2b+a-2b-2=4.又ab>a-b(a>1,b>0),∴ab-a-b=2.答案:D6.已知函数f(x)=|2x-1|,af(c)>f(b),则下列结论中,一定成立的是()A.a<0,b<0,c<0B.a<0,b≥0,c>0C.2-a<2cD.2a+2c<2解析:作出函数f(x)=|2x-1|的图象如右图中实线所示,又af(c)>f(b),结合图象知f(a)<1,a<0,c>0.∴0<2a<1,∴f(a)=|2a-1|=1-2a.∴f(c)<1,∴0f(c),即1-2a>2c-1.∴2a+2c<2.答案:D7.设函数f(x)=-,[x]表示不超过x的最大整数,则函数y=[f(x)]的值域是().A.{0,1}B.{0,-1}C.{-1,1}D.{1,1}解析由f(x)=-=1--=-,由于(2x+1)在R上单调递增,所以-在R上单调递增,所以f(x)为增函数,由于2x>0,当x→∞-,2x→0,∴f(x)>-,当x→∞→+,0,∴f(x)<,∴-<f(x)<,∴y=[f(x)]={0,-1}.答案B二、填空题8.8×+(×)6=________.解析:原式=2×2+6=2+22×33=2+4×27=110.答案:1109.若直线y=2a与函数y=|ax-1|(a>0,且a≠1)的图象有两个公共点,则a的取值范围是________.解析(数形结合法)由图象可知0<2a<1,∴0<a<.答案10.若函数y=2-x+1+m的图象不经过第一象限,则m的取值范围是________.解析:函数y=2-x+1+m=()x-1+m, 函数的图象不经过第一象限,∴()0-1+m≤0,即m≤-2.答案:(∞-,-2]11.若函数f(x)=ax-x-a(a>0,且a≠1)有两个零点,则实数a的取值范围是________.解析令ax-x-a=0即ax=x+a,若01,y=ax与y=x+a的图象如图所示.答案(1∞,+)12.已知正数a满足a2-2a-3=0,函数f(x)=ax,若实数m、n满足f(m)>f(n),则m、n的大小关系为________.解析: a2-2a-3=0,∴a=3或a=-1(舍).函数f(x)=ax在R上递增,由f(m)>f(n)得m>n.答案:m>n三、解答题13.已知f(x)=ex-e-x,g(x)=ex+e-x(e=2.71828…)(1)求[f(x)]2-[g(x)]2的值;(2)若f(x)f(y)=4,g(x)g(y)=8,求的值.解析(1)[f(x)]2-[g(x)]2=(ex-e-x)2-(ex+e-x)2=(e2x-2+e-2x)-(e2x+2+e-2x)=-4.(2)f(x)f(y)=(ex-e-x)(ey-e-y)=ex+y+e-x-y-ex-y-e-x+y=[ex+y+e-(x+y)]-[ex-y+e-(x-y)]=g(x+y)-g(x-y)∴g(x+y)-g(x-y)=4①同理,由g(x)g(y)=8,可得g(x+y)+g(x-y)=8,②由①②解得g(x+y)=6,g(x-y)=2,∴=3.14.已知函数f(x)=b·ax(其中a,b为常量,且a>0,a≠1)的图象经过点A(1,6),B(3,24).(1)求f(x);(2)若不等式()x+()x-m≥0在x∈(∞-,1]时恒成立,求实数m的取值范围.解析:(1)把A(1,6),B(3,24)代入f(x)=b·ax,得结合a>0且a≠1,解得∴f(x)=3·2x.(2)要使()x+()x≥m在(∞-,1]上恒成立,只需保证函数y=()x+()x在(∞-,1]上的最小值不小于m即可. 函数y=()x+()x在(∞-,1]上为减函数,∴当x=1时,y=()x+()x有最小值.∴只需m≤即可.∴m的取值范围(∞-,]15.已知函数f(x)=ax2-4x+3.(1)若a=-1,求f(x)的单调区间;(2)若f(x)有最大值3,求a的值.解析:(1)当a=-1时,f(x)=-x2-4x+3,令t=-x2-4x+3,由于t(x)在(∞-,-2)上单调递增,在[-2∞,+)上单调递减,...