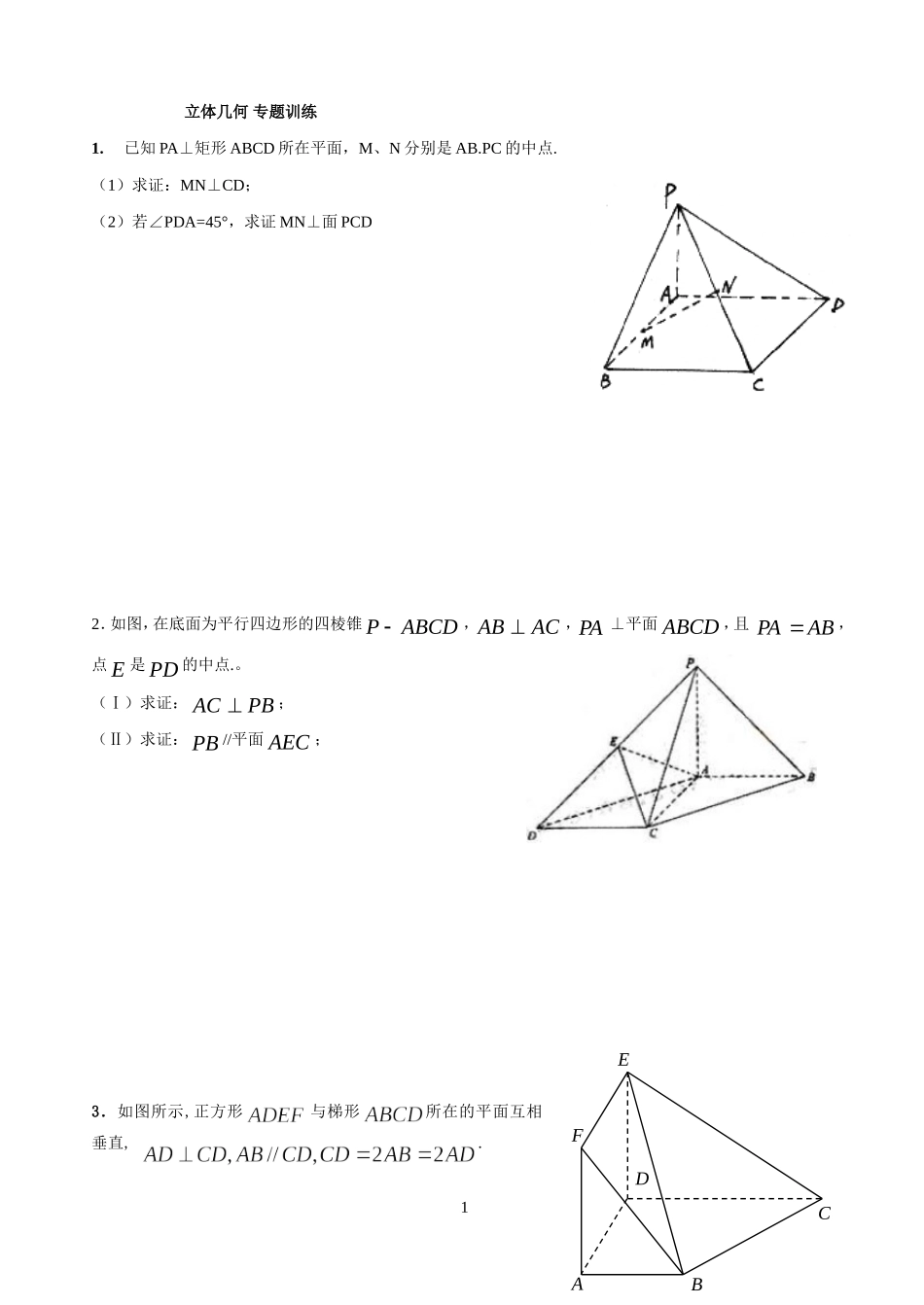
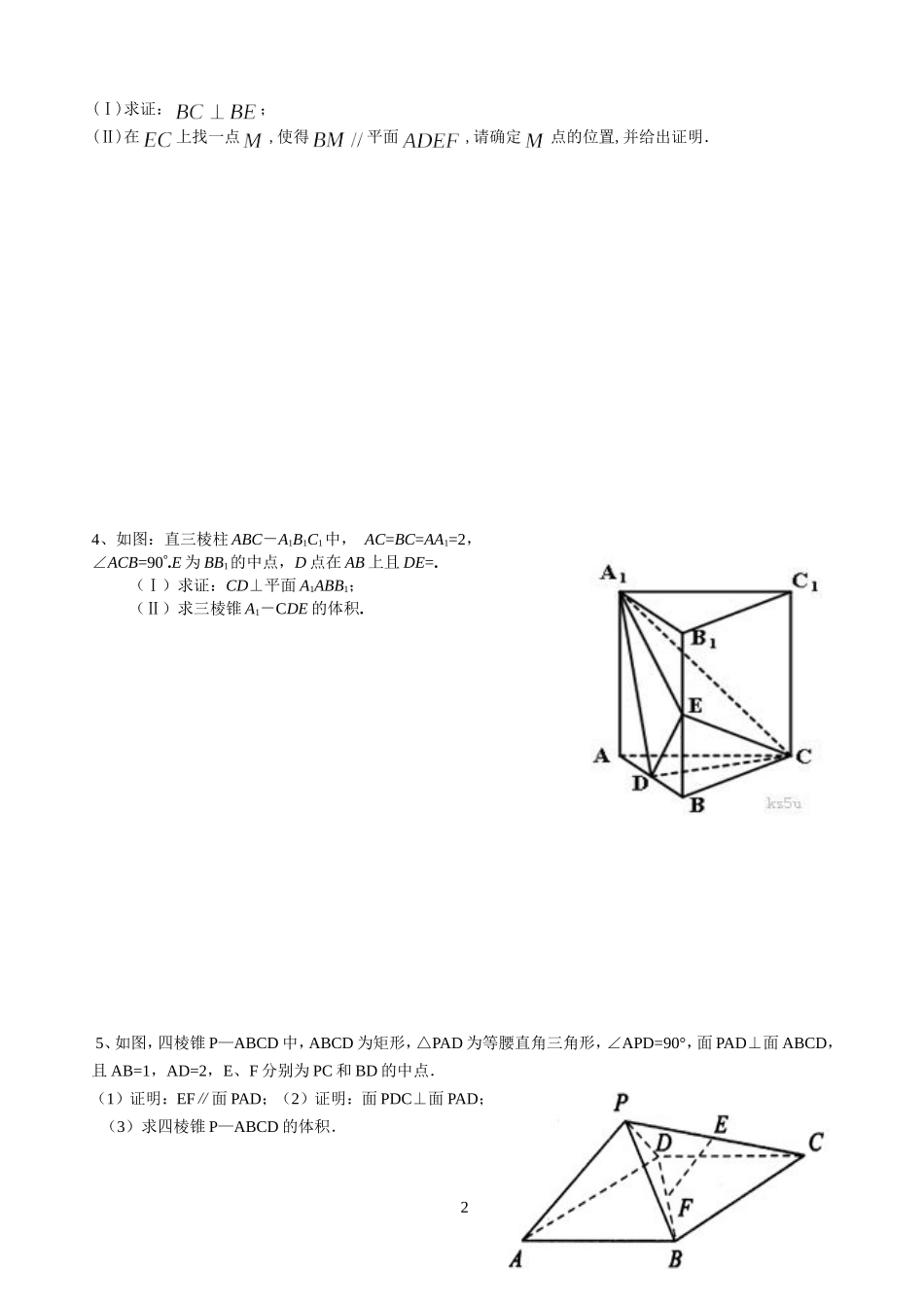
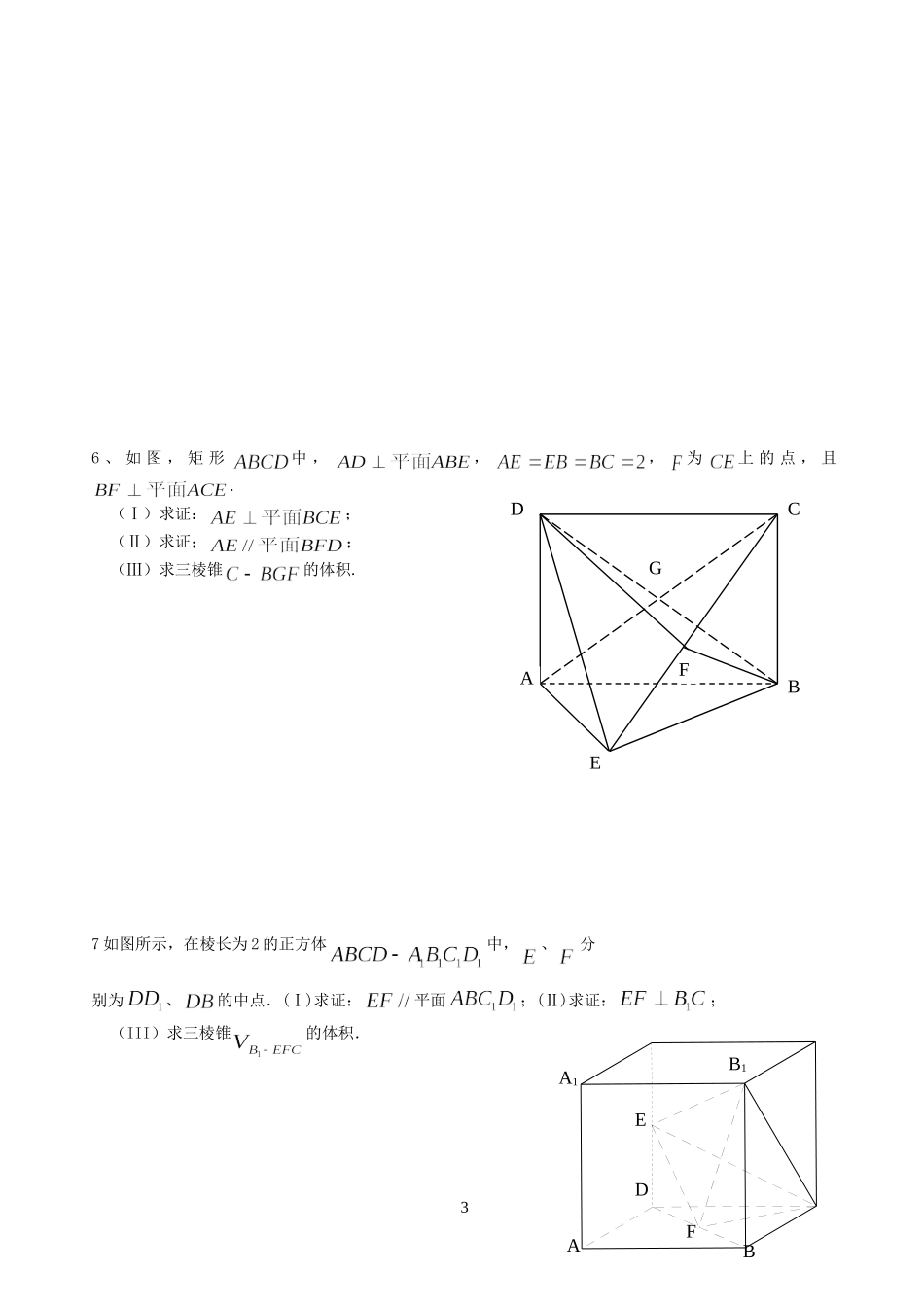
立体几何专题训练1.已知PA⊥矩形ABCD所在平面,M、N分别是AB.PC的中点.(1)求证:MN⊥CD;(2)若∠PDA=45°,求证MN⊥面PCD2.如图,在底面为平行四边形的四棱锥ABCDP,ACAB,PA⊥平面ABCD,且ABPA,点E是PD的中点.。(Ⅰ)求证:PBAC;(Ⅱ)求证:PB//平面AEC;3.如图所示,正方形与梯形所在的平面互相垂直,.1EBACDF(Ⅰ)求证:;(Ⅱ)在上找一点,使得平面,请确定点的位置,并给出证明.4、如图:直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90.E为BB1的中点,D点在AB上且DE=.(Ⅰ)求证:CD⊥平面A1ABB1;(Ⅱ)求三棱锥A1-CDE的体积.5、如图,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.(1)证明:EF∥面PAD;(2)证明:面PDC⊥面PAD;(3)求四棱锥P—ABCD的体积.26、如图,矩形中,,,为上的点,且.(Ⅰ)求证:;(Ⅱ)求证;;(Ⅲ)求三棱锥的体积.7如图所示,在棱长为2的正方体中,、分别为、的中点.(Ⅰ)求证:平面;(Ⅱ)求证:;(III)求三棱锥的体积.3ABCDEFGABDEFA1B1ABCDPEF8、如图,在四棱锥中,底面ABCD是正方形,侧棱底面ABCD,,E是PC的中点,作交PB于点F.(I)证明:PA∥平面EDB;(II)证明:PB⊥平面EFD;(III)求三棱锥的体积.9已知在侧棱垂直于底面三棱柱ABC—A1B1C1中AC=3,AB=5,(Ⅰ)求证:(Ⅱ)求证:AC1//平面CDB1;(Ⅲ)求三棱锥A1—B1CD的体积.410.如图,四棱锥PABCD中,四边形ABCD为矩形,PAD为等腰三角形,90APD,平面PAD平面ABCD,且1,2,ABADE.F分别为PC和BD的中点.(1)证明://EF平面PAD;(2)证明:平面PDC平面PAD;(3)求四棱锥PABCD的体积.11.如图,四棱锥中,平面,四边形是矩形,、分别是、的中点.若,.(Ⅰ)求证:平面;(Ⅱ)求点到平面的距离;51A1B1CABDC第18题图12、如图,在三棱柱111ABCABC中,3AC,平面,4BC,5AB,14AA,点D是AB的中点,(1)求证:1ACBC;(2)求证:11ACCDB平面;(3)求三棱锥11CCDB的体积。6