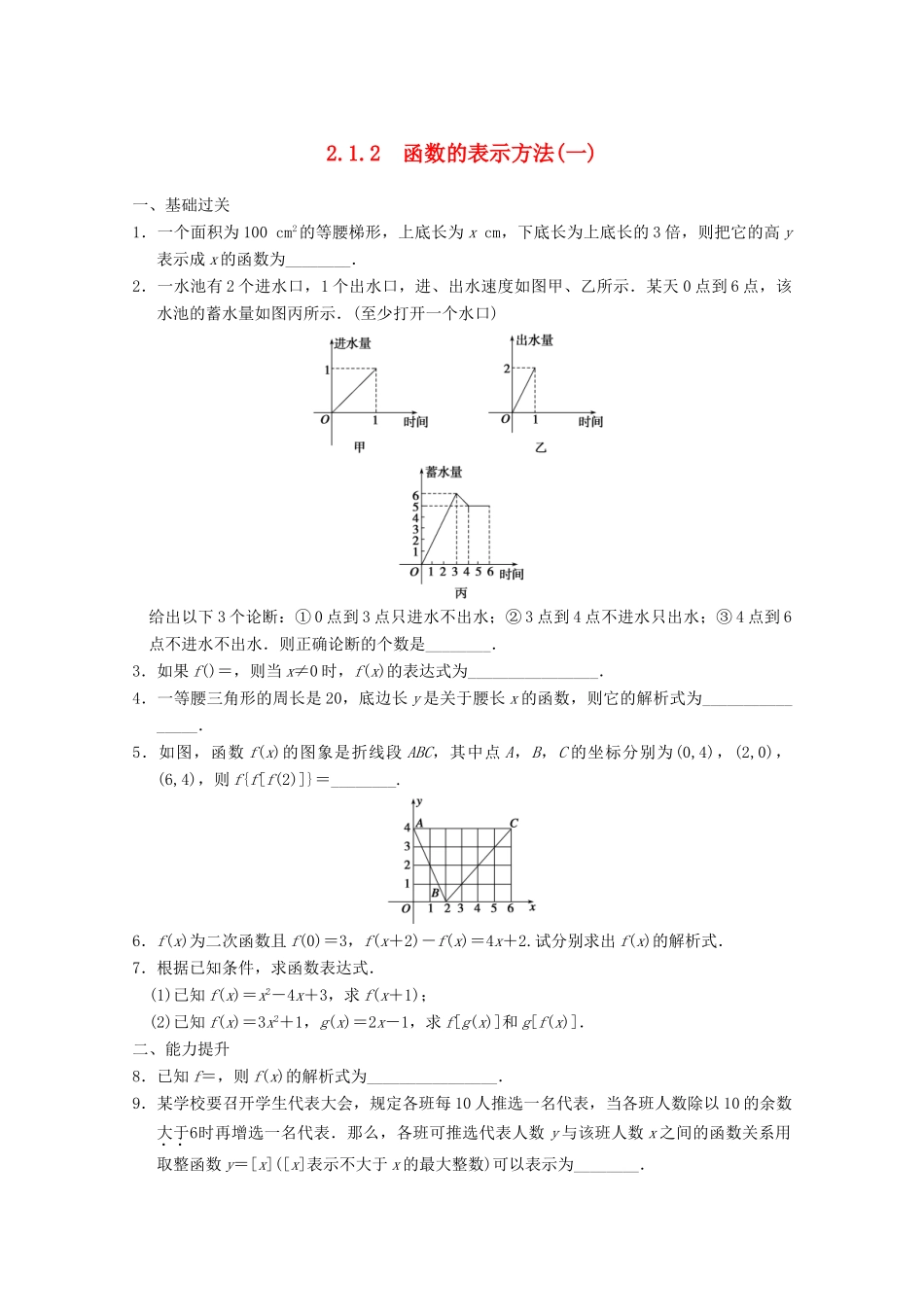
2.1.2函数的表示方法(一)一、基础过关1.一个面积为100cm2的等腰梯形,上底长为xcm,下底长为上底长的3倍,则把它的高y表示成x的函数为________.2.一水池有2个进水口,1个出水口,进、出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水.则正确论断的个数是________.3.如果f()=,则当x≠0时,f(x)的表达式为________________.4.一等腰三角形的周长是20,底边长y是关于腰长x的函数,则它的解析式为________________.5.如图,函数f(x)的图象是折线段ABC,其中点A,B,C的坐标分别为(0,4),(2,0),(6,4),则f{f[f(2)]}=________.6.f(x)为二次函数且f(0)=3,f(x+2)-f(x)=4x+2.试分别求出f(x)的解析式.7.根据已知条件,求函数表达式.(1)已知f(x)=x2-4x+3,求f(x+1);(2)已知f(x)=3x2+1,g(x)=2x-1,求f[g(x)]和g[f(x)].二、能力提升8.已知f=,则f(x)的解析式为________________.9.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为________.①y=[]②y=[]③y=[]④y=[]10.已知f(x)是一次函数,若f(f(x))=4x+8,则f(x)的解析式为________________________.11.有一种螃蟹,从海上捕获不放养最多只能存活两天,如果放养在塘内,可以延长存活时间,但每天也有一定数量的蟹死去,假设放养期内蟹的个体重量基本保持不变.现有一经销商,按市场价收购了这种活蟹1000kg放养在塘内,此时市场价为每千克30元.据测算,此后每千克活蟹的市场价每天可上升1元.但是,放养一天需各种费用支出400元,且平均每天还有10kg蟹死去,假定死蟹均于当天全部售出,售价都是每千克20元.(1)设x天后每千克活蟹的市场价为P元,写出P关于x的函数关系式;(2)如果放养x天后将活蟹一次性出售,并记1000kg蟹的销售总额为Q元,写出Q关于x的函数关系式.三、探究与拓展12.设f(x)是R上的函数,且满足f(0)=1,并且对任意实数x,y,有f(x-y)=f(x)-y(2x-y+1),求f(x)的解析式.答案1.y=(x>0)2.13.f(x)=4.y=20-2x(5