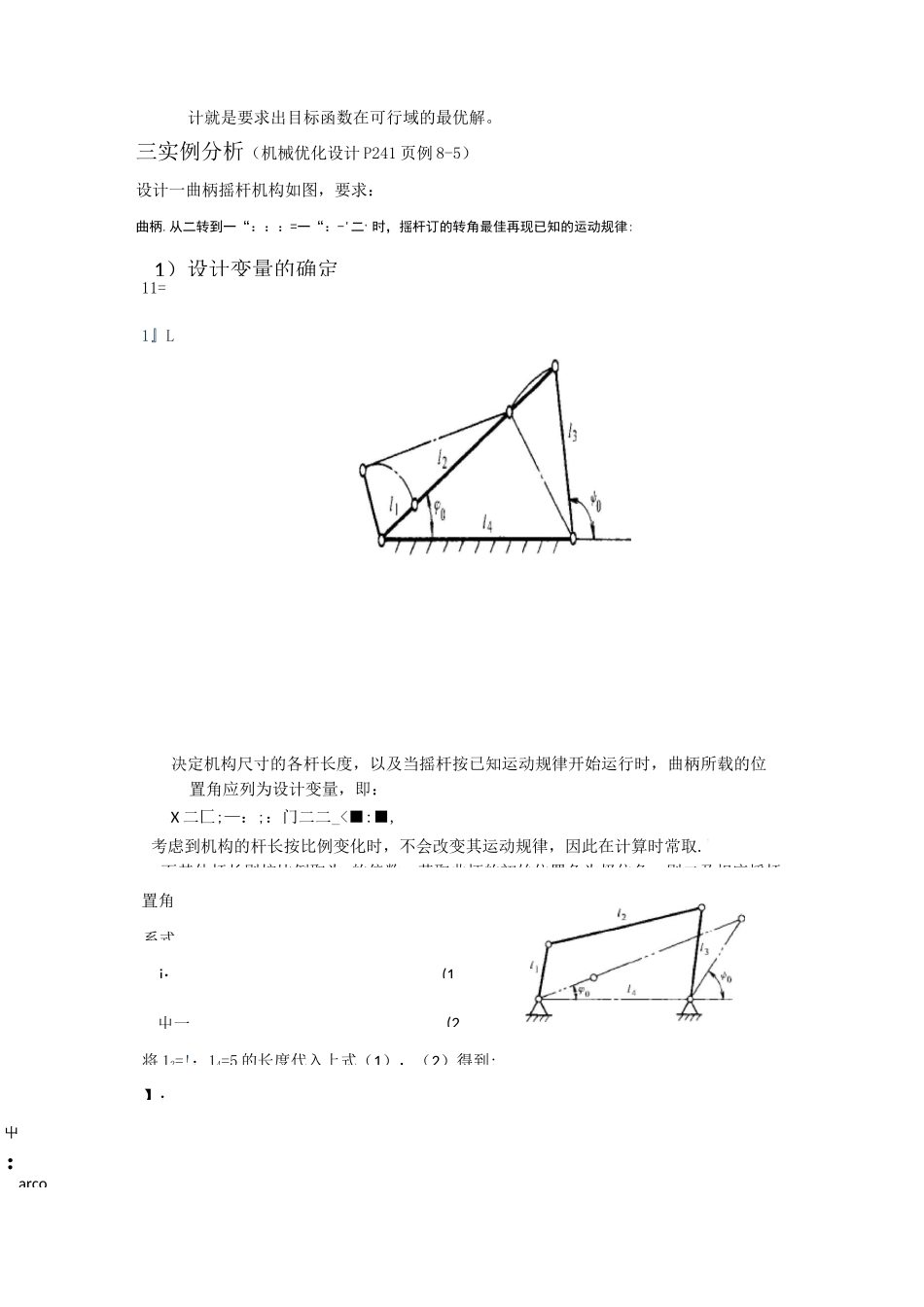
机械优化设计在matlab中的应用东南大学机械工程学院**一优化设计目的:在生活和工作中,人们对于同一个问题往往会提出多个解决方案,并通过各方面的论证从中提取最佳方案。最优化方法就是专门研究如何从多个方案中科学合理地提取出最佳方案的科学。由于优化问题无所不在,目前最优化方法的应用和研究已经深入到了生产和科研的各个领域,如土木工程、机械工程、化学工程、运输调度、生产控制、经济规划、经济管理等,并取得了显著的经济效益和社会效益。二优化设计步骤:1.机械优化设计的全过程一般可以分为如下几个步骤:1)建立优化设计的数学模型;2)选择适当的优化方法;3)编写计算机程序;4)准备必要的初始数据并伤及计算;5)对计算机求得的结果进行必要的分析。其中建立优化设计数学模型是首要的和关键的一步,它是取得正确结果的前提。优化方法的选取取决于数学模型的特点,例如优化问题规模的大小,目标函数和约束函数的性态以及计算精度等。在比较各种可供选用的优化方法时,需要考虑的一个重要因素是计算机执行这些程序所花费的时间和费用,也即计算效率。2.建立数学模型的基本原则与步骤①设计变量的确定;设计变量是指在优化设计的过程中,不断进行修改,调整,一直处于变化的参数称为设计变量。设计变量的全体实际上是一组变量,可用一个列向量表示:x二,.,,-..:.II。②目标函数的建立;选择目标函数是整个优化设计过程中最重要的决策之一。当对某以设计性能有特定的要求,而这个要求有很难满足时,则针对这一性能进行优化会得到满意的效果。目标函数是设计变量的函数,是一项设计所追求的指标的数学反映,因此它能够用来评价设计的优劣。目标函数的一般表达式为:f(x)=,要根据实际的设计要求来设计目标函数。③约束条件的确定。一个可行性设计必须满足某些设计限制条件,这些限制条件称为约束条件,简称约束。由若干个约束条件构成目标函数的可行域,而可行域内的所有设计点都是满足设计要求的,一般情况下,其设计可行域可表示为在可行域中,任意设计点满足全部约束条件,称为可行解,但不是最优解,而优化设11=1』L1)设计变量的确定决定机构尺寸的各杆长度,以及当摇杆按已知运动规律开始运行时,曲柄所载的位置角应列为设计变量,即:X二匚;—:;:门二二_<■:■,考虑到机构的杆长按比例变化时,不会改变其运动规律,因此在计算时常取.',而其他杆长则按比例取为.的倍数。若取曲柄的初始位置角为极位角,则二及相应摇杆置角系式i:(1屮一(2将12=!;14=5的长度代入上式(1),(2)得到:】:屮:=arco计就是要求出目标函数在可行域的最优解。三实例分析(机械优化设计P241页例8-5)设计一曲柄摇杆机构如图,要求:曲柄.从二转到一“:::=一“:-'二,时,揺杆订的转角最佳再现已知的运动规律:(32)目标函数的建立目标函数可根据已知的运动规律与机构实际运动规律之间的偏差最小为指标来建立,即f(x)=n_屮_疋::一min式中屮三一期望输出角,屮::=V.〔「:);m—输入角等分数;屮:一实际输出角,由下图得:a)0W<屮=(皿_囚_囲iIit_%+區式中西=arcos(已=arcosf将输入角分成30等分,并用近似公式计算,可得目标函数的表达式:f(x)W二壯:-巴:由题意知,传动角的变化范围是三7■三-三,,则上式中变量的最后形式可以写成:览一一3cp=虧时的机构实际输出角,有式⑶可知其计算公式为:屮i=-n-ai-pt(nt<2n)需pL=%/26-lOccsqp!/26—lOcoscpt+24Bi=arcosI\10^/26-10coscpL将::带入(4)(5)2J26—lOcostpi心屮三:为当二二二时的理想输出角,其值在题目中已经给出:2X(q>{-npa)A2+353)约束条件的确①曲柄摇杆机构应满足曲柄存在条件,可得Si区)=h—k—02(葢)=—lg—Sa00=h—L三。Sife}=I]+Ij—lg—1卫兰0丽何=h+h——一L—g百仗〕=I]十—k—k—②曲柄摇杆机构的传动角下::::胃口下...鑒:之g?w=aregsfc)=7把约束条件简化(:.=5,-三,JgiW=1-<0氏〔刃=i—世冬0Sg00=1-5兰0giW=S-<0g5W=阳一x;-4<0gfiW=毛一Kj-4<&arcoarea26—10coscpt+症一症—下论乂13+1J-(11+1J2nn;miH-arC0E<0x=g7(x)二云十云—1.414阳—16<0ga(x)=36--1,414Xi<0其中E满足条件,故最后一共...