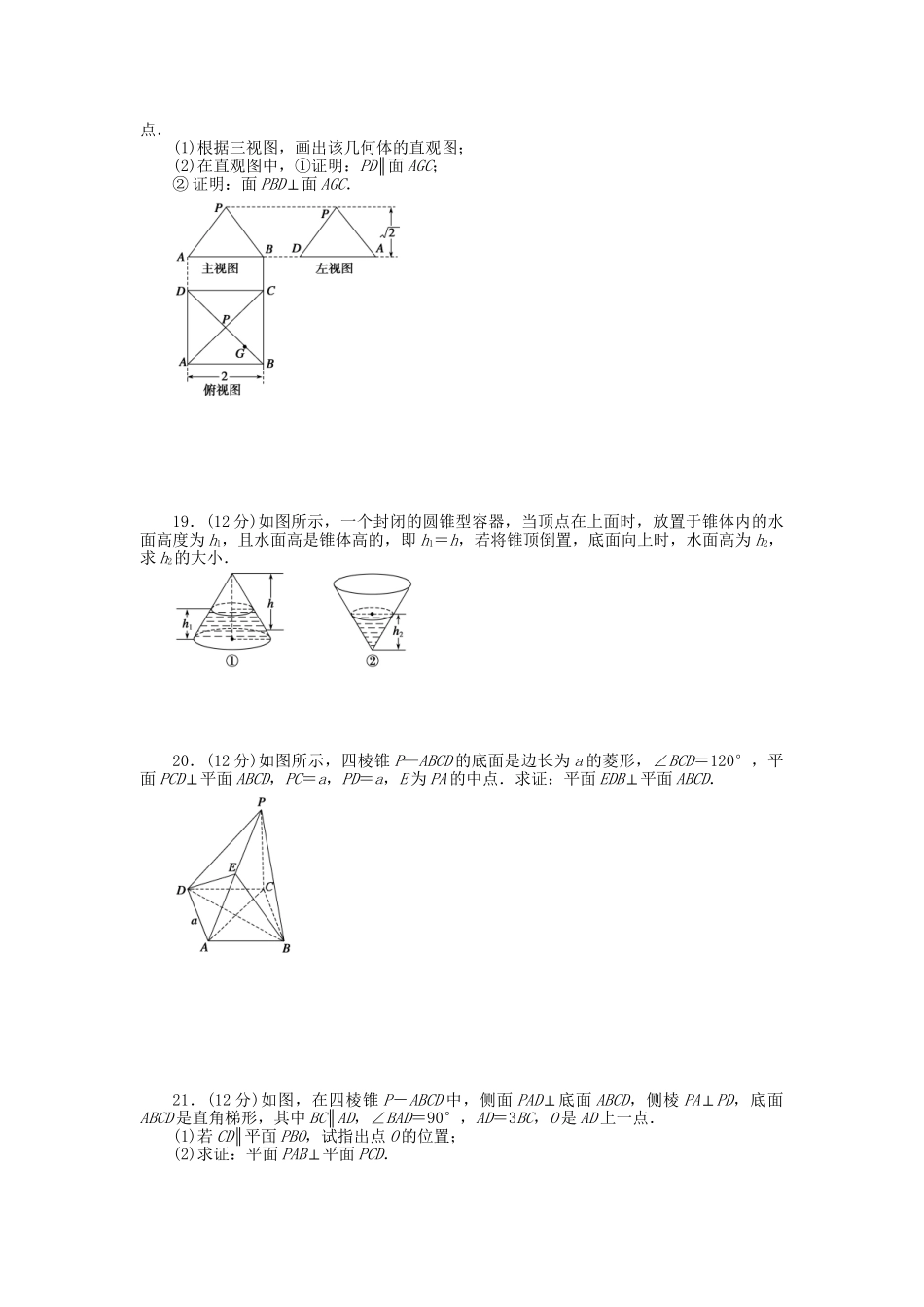
第一章立体几何初步(B)(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分)1.在空间四边形ABCD的边AB,BC,CD,DA上分别取E、F、G、H四点,如果EF,GH交于一点P,则()A.P一定在直线BD上B.P一定在直线AC上C.P一定在直线AC或BD上D.P既不在直线AC上,也不在直线BD上2.下列说法不正确的是()A.圆柱的侧面展开图是一个矩形B.圆锥的过轴的截面是一个等腰三角形C.直角三角形绕它的一条边旋转一周形成的曲面围成的几何体是圆锥D.圆台平行于底面的截面是圆面3“”.水平放置的正方体的六个面分别用前面、后面、上面、下面、左面、右面表示,“如图所示,是一个正方体的表面展开图,若图中2”在正方体的上面,则这个正方体的下面是()A.0B.9C.快D.乐4.如图,△O′A′B′是水平放置的△OAB的直观图,则△AOB的面积是()A.6B.3C.6D.125.下列命题正确的是()A.一条直线与一个平面平行,它就和这个平面内的任意一条直线平行B.平行于同一个平面的两条直线平行C.平面外的两条平行直线中的一条与一个平面平行,则另一条直线也与此平面平行D.与两个相交平面的交线平行的直线,必平行于这两个平面6.如果OA∥O1A1,OB∥O1B1,那么∠AOB与∠A1O1B1()A.相等B.互补C.相等或互补D.以上均不对7.正方体ABCD-A1B1C1D1中与AD1垂直的平面是()A.平面DD1C1CB.平面A1DB1C.平面A1B1C1D1D.平面A1DB8.一个几何体的三视图如图所示,则这个几何体的体积等于()A.4B.6C.8D.129.若圆台两底面周长的比是1∶4,过高的中点作平行于底面的平面,则圆台被分成两部分的体积比是()A.B.C.1D.10.设α、β是两个不同的平面,l是一条直线,以下命题正确的是()A.若l⊥α,α⊥β,则lβB.若l∥α,α∥β,则lβC.若l⊥α,α∥β,则l⊥βD.若l∥α,α⊥β,则l⊥β11.已知从球的一内接长方体的一个顶点出发的三条棱长分别为3,4,5,则此球的表面积为()A.25πB.50πC.125πD.均不正确12.如图,在空间四边形ABCD中,E、H分别是AB、AD的中点,F、G分别是CB、CD上的点,且==,若BD=6cm,梯形EFGH的面积为28cm2,则平行线EH、FG间的距离为()A.8cmB.6cmC.4cmD.9cm二、填空题(本大题共4小题,每小题5分,共20分)13.设平面α∥平面β,A、C∈α,B、D∈β,直线AB与CD交于点S,且点S位于平面α,β之间,AS=8,BS=6,CS=12,则SD=________.14.已知用斜二测画法,画得正方形的直观图的面积为18,则原正方形的面积为________.15.空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.①若AC=BD,则四边形EFGH的形状是______;②若AC⊥BD,则四边形EFGH的形状是______.16.如图,四棱锥S-ABCD中,底面ABCD为平行四边形,E是SA上一点,当点E满足条件:____________时,SC∥平面EBD.三、解答题(本大题共6小题,共70分)17.(10分)画出如图所示的四边形OABC的直观图.(要求用斜二测画法,并写出画法)18.(12分)某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.(1)根据三视图,画出该几何体的直观图;(2)在直观图中,①证明:PD∥面AGC;②证明:面PBD⊥面AGC.19.(12分)如图所示,一个封闭的圆锥型容器,当顶点在上面时,放置于锥体内的水面高度为h1,且水面高是锥体高的,即h1=h,若将锥顶倒置,底面向上时,水面高为h2,求h2的大小.20.(12分)如图所示,四棱锥P—ABCD的底面是边长为a的菱形,∠BCD=120°,平面PCD⊥平面ABCD,PC=a,PD=a,E为PA的中点.求证:平面EDB⊥平面ABCD.21.(12分)如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.(1)若CD∥平面PBO,试指出点O的位置;(2)求证:平面PAB⊥平面PCD.22.(12分)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.(1)证明:EF∥平面PAD;(2)求三棱锥E-ABC的体积V.第一章立体几何初步(B)答案1.B[如图, P∈HG,HG面ACD,∴P∈面ACD,同理P∈面BAC,面BAC∩面ACD=AC;∴P∈AC,选B.]2.C3.B4.D[△OAB为直角...