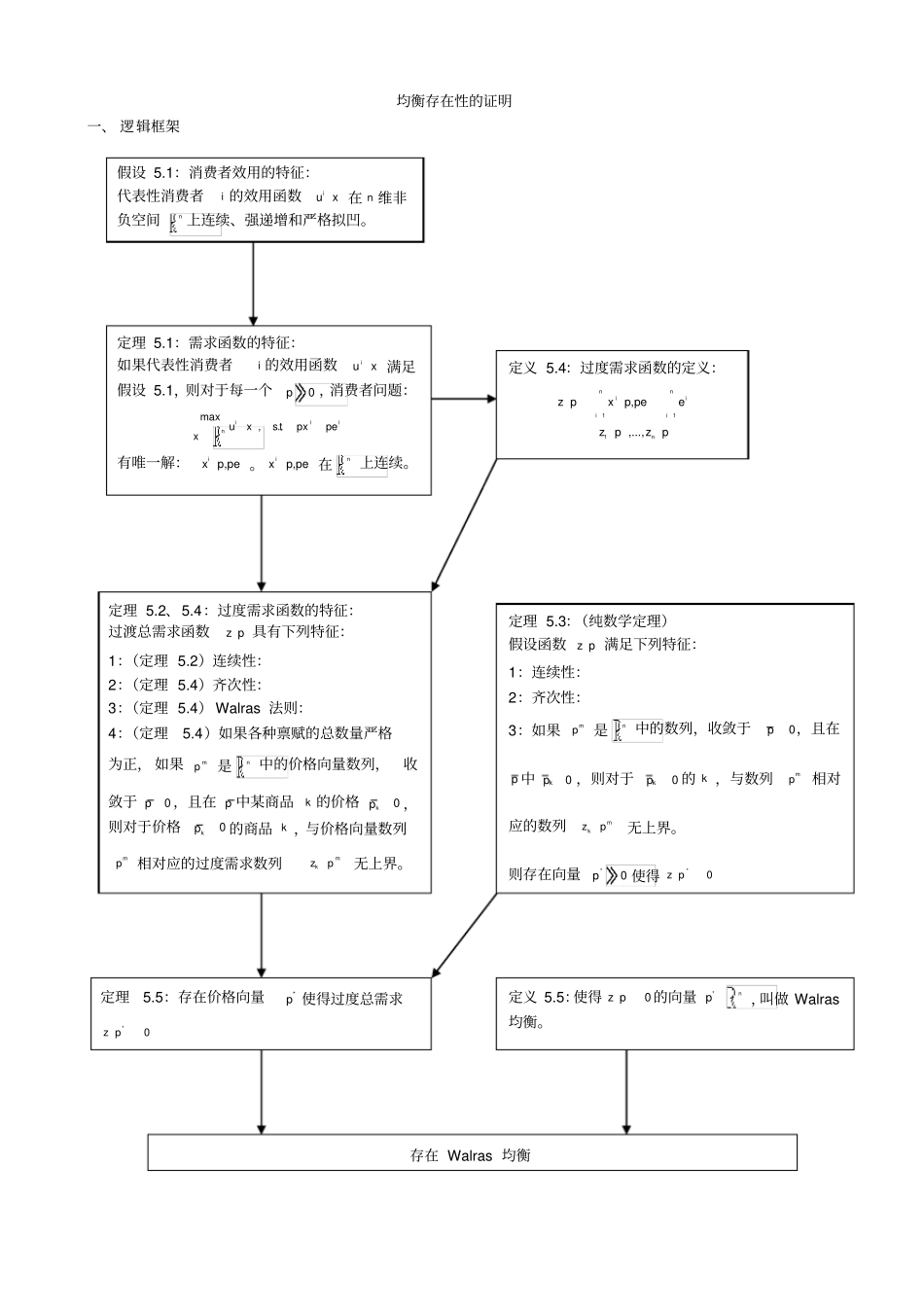
均衡存在性的证明一、逻辑框架假设5.1:消费者效用的特征:代表性消费者i的效用函数iux在n维非负空间n上连续、强递增和严格拟凹。定理5.1:需求函数的特征:如果代表性消费者i的效用函数iux满足假设5.1,则对于每一个0p,消费者问题:max,..iiinuxstxpxpe有唯一解:ixp,pe。ixp,pe在n上连续。定义5.4:过度需求函数的定义:111,...,nniiiinzpxp,peezpzp定理5.2、5.4:过度需求函数的特征:过渡总需求函数zp具有下列特征:1:(定理5.2)连续性:2:(定理5.4)齐次性:3:(定理5.4)Walras法则:4:(定理5.4)如果各种禀赋的总数量严格为正,如果mp是n中的价格向量数列,收敛于0p,且在p中某商品k的价格0kp,则对于价格0kp的商品k,与价格向量数列mp相对应的过度需求数列mkzp无上界。定理5.3:(纯数学定理)假设函数zp满足下列特征:1:连续性:2:齐次性:3:如果mp是n中的数列,收敛于0p,且在p中0kp,则对于0kp的k,与数列mp相对应的数列mkzp无上界。则存在向量*p0使得0*zp定理5.5:存在价格向量*p使得过度总需求0*zp定义5.5:使得0zp的向量*np,叫做Walras均衡。存在Walras均衡证明定理5.4(3):如果每个消费者的效用函数都满足假设5.1,并且各种禀赋的总数量严格为正,10Iiie,如果mp是n中的价格向量数列,收敛于0p,且在p中某商品k的价格0kp,则对于价格0kp的商品k,与价格向量数列mp相对应的过度需求数列mkzp无上界。解释:1.mp定义在n中,即对于所有的m,有0mp。2.当m,mpp,p的特征为0p且0p;同时,由于在p中某些坐标为零,0kp,所以,p并不严格大于零向量,如,1211,,...,,0,,...,kknpppppp。也就是说,当m时,mpp,0mkp。3.p中为零的坐标,第k个坐标,k可能等于k,也可能不等于k,对一切等于零的坐标或商品,0kp,其需求为无穷大。由于当m时mkkpp,所以,mkp,即mkp无上界。证明:设严格为正的价格数列mp收敛于0p,对于某商品k,有0kp。由于10Iiie,且0p,所以Iii=1pe>0,IIiii=1i=1pepe>0,所以,至少一位消费者有ipe>0。对应于价格向量数列mp,该消费者有需求数列immixp,pe:对于所有的m,argmax,..immiiiinustxp,pexpxpex我们要证明该消费者的需求数列无上界。反证法。设immixp,pe有界,则有收敛子数列。假设数列immixp,pe收敛于*x,即当m时,*mimmixxp,pex。对于所有的m,有mmmipxpe。有limlimmmmimmxpppxpe,得*0ipepx。令*0,...,0,1,0,...,0xx,其中第k项为1。效用函数强递增,因此有,*uuxx。且有*0ipxpxpe**1,0*0,...,0,1,0,...,0100nkjjjkppipxpxppxpxpe效用函数连续,所以,存在一个0,1t,使得*utuxx且*tipxpxpe为什么设计tx?由于在m时,mpp,*mxx,所以,在m足够大时,有mutuxx,mmtipxpe,所以,mx不是消费当m足够大时,mx在*x的邻域内。mx*xtx*x者问题在mp下的解。这与假设相矛盾,所以,与特征为收敛于0p且在p中某商品k的价格0kp的价格向量数列mp相对应的需求数列mx无上界。1,...,mmmnxxx无上界,意味着其全部或部分或至少一个元素无上界。假设是商品k的需求mkx无上界。由于此消费者的收入mipe收敛于ipe,所以收入数列mipe有界。也就意味着mmikkpxpe,因为mkx无上界,所以0mkp,即lim0mkkmpp。由于对商品k的需求mkx无上界,而此商品的供给固定,所以其过度需求数列mkzp无上界。定理5.3:(纯数学定理)假设函数zp满足下列特征:1:连续性:2:齐次性:3:如果mp是n中的数列,收敛于0p,且在p中0kp,则对于0kp的k,与数列mp相对应的数列mkzp无上界。则存在向量*p0使得0zp解题思想:应用Brouwer不动点定理解题步骤:1、构造单纯形用1,...,nPPP表示各商品的货币价格。用1111,...,,...,mnnnmmmmPPppPPp表示相对价格。函数zp满足齐次性,11nmmPzPzPzp,寻找使0zP的解,等同于寻找使0zp的解。相对价格向量的特点:11nkkp,价格向量为单纯形中的点。但是,应用不动点定理,函数在定义域上必须是连续的,但是,当某些商品的价格为零如图中的价格向量2p时,该商品的需求为无穷大,呈现不连续的特征。必须把这种情况排除除去,即设法保证0p。商品1商品2商品31p2p定理A1.11:Brouwer不动点定理设nS是非空集、紧集和凸集。设:fSS是连续映射,那么在集合S中,存在...