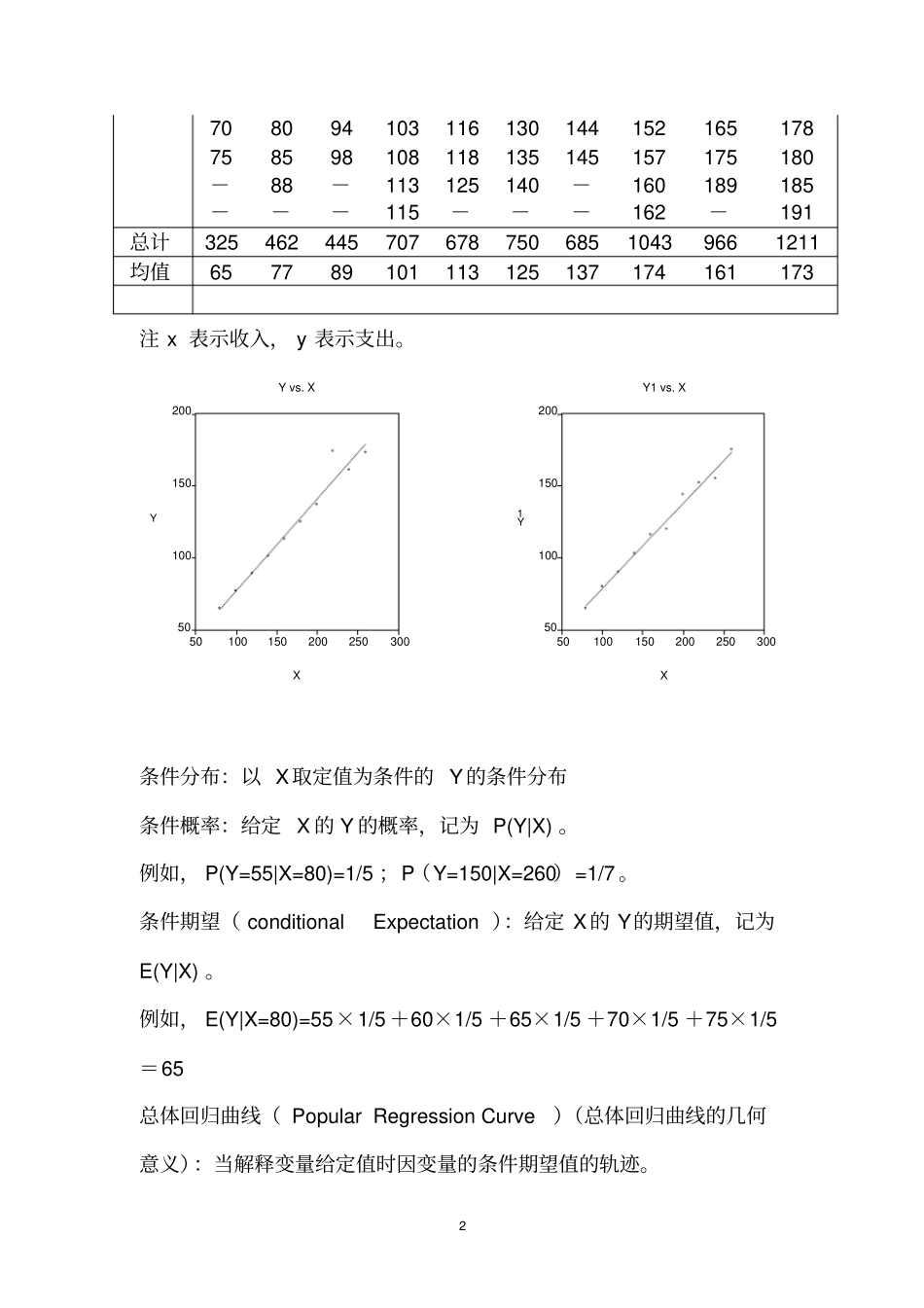
1第三部分初计量经济(13周)经典单方程计量经济模型:一元线形回归模型经典单方程计量经济模型:多元线形回归模型经典单方程计量经济模型:放宽基本假定模型第一章一元线性回归(双变量)(1)回归分析的基本概念(2)前提建设(3)参数估计:OLS的参数估计ML的参数估计(4)统计检验(5)预测(6)时间案例与操作(7)思考与作业§1经典正态线性回归模型(CNLRM)1、一个例子XY801001201401601802002202402605565798010211012013513715060708493107115136137145152657490951101201401401551752708094103116130144152165178758598108118135145157175180-88-113125140-160189185---115---162-191总计32546244570767875068510439661211均值657789101113125137174161173注x表示收入,y表示支出。5010015020050100150200250300XYYvs.X5010015020050100150200250300XY1Y1vs.X条件分布:以X取定值为条件的Y的条件分布条件概率:给定X的Y的概率,记为P(Y|X)。例如,P(Y=55|X=80)=1/5;P(Y=150|X=260)=1/7。条件期望(conditionalExpectation):给定X的Y的期望值,记为E(Y|X)。例如,E(Y|X=80)=55×1/5+60×1/5+65×1/5+70×1/5+75×1/5=65总体回归曲线(PopularRegressionCurve)(总体回归曲线的几何意义):当解释变量给定值时因变量的条件期望值的轨迹。3总结总体:总体函数:PRF:Yi=1+2Xi+ui=E(Y|Xi)+ui总体方程:PRF:Yi=1+2Xi=E(Y|Xi)样本:样本函数:SRF:iY=1?+2?iX+iu?=iY?+iu?样本方程:SRF:iY=1?+2?iX+iu?=iY?2、总体回归函数(PRF)E(Y|Xi)=f(Xi)当PRF的函数形式为线性函数,则有,E(Y|Xi)=1+2Xi其中1和2为未知而固定的参数,称为回归系数。1和2也分别称为截距和斜率系数。上述方程也称为线性总体回归函数。43、PRF的随机设定将个别的YI围绕其期望值的离差(Deviation)表述如下:ui=Yi-E(Y|Xi)或Yi=E(Y|Xi)+uiPRF:Yi=1+2Xi+ui=E(Y|Xi)+ui其中ui是一个不可观测的可正可负的随机变量,称为随机扰动项或随机误差项。4、“线性”的含义“线性”可作两种解释:对变量为线性,对参数为线性。本课“线性”回归一词总是指对参数为线性的一种回归(即参数只以它的1次方出现)。模型对参数为线性?模型对变量为线性?是不是是LRMLRM不是NLRMNLRM注:LRM=线性回归模型;NLRM=非线性回归模型。看几个例子:5、随机干扰项的意义(补充内容)随机扰动项是从模型中省略下来的而又集体地影响着Y的全部变量的替代物。显然的问题是:为什么不把这些变量明显地引进到模型中5来?换句话说,为什么不构造一个含有尽可能多个变量的复回归模型呢?理由是多方面的:(1)理论的含糊性(2)数据的欠缺(3)核心变量与周边变量(4)内在随机性(5)替代变量(6)省略原则(7)错误的函数形式总之把所有没有模型中没有包含,但有关的变量全部纳入干扰项之中。6、样本回归函数(SRF)(1)样本回归函数iY?=1?+2?iX其中Y?=E(Y|Xi)的估计量;1?=1的估计量;2?=2的估计量。估计量(Estimator):一个估计量又称统计量,是指一个规则、公式或方法,是用已知的样本所提供的信息去估计总体参数。在应用中,由估计量算出的数值称为估计值。样本回归函数的随机形式为:SRF:iY=1?+2?iX+iu?=iY?+iu?其中iu?表示(样本)残差项(residual)。6(2)样本回归线的几何意义7、经典线性回归模型(CLRM)的基本假定:假定1:干扰项的均值为零。即,E(ui|Xi)=0假定2:同方差性或ui的方差相等。即,Var(ui|Xi)=2假定3:各个干扰项无自相关。即,Cov(ui,uj|Xi,Xj)=0假定4:ui和Xi的协方差为零。即,Cov(ui,Xi)=E(uiXi)=0假定5:回归模型对参数而言是线性的假定6:2~(,)iuNu§2估计问题(和2)一、普通最小二乘法1、问题:PRF:Yi=1+2Xi+uiSRF:iY=1?+2?iX+iu?=iY?+iu?iu?=iY-iY?=iY-(1?+2?iX)XiXPRF:E(Y|Xi)=1+2XiSRF:iY?=1?+2?iXiu?iuYiYiY?E(Y|Xi)7minf(1?,2?)=miniu?2=min[iY-(1?+2?iX)]22、正规方程(Normalequation)由1?f=0,以及2?f=0得到的方程组称为正规方程。即,iY=n1?+2?iXiYiX=1?iX+2?iX2二、的估计1、公式:解上述正规方程组得到1?和2?估计值:222)())((?iiiiiixyxXXYYXXXY2?1?...