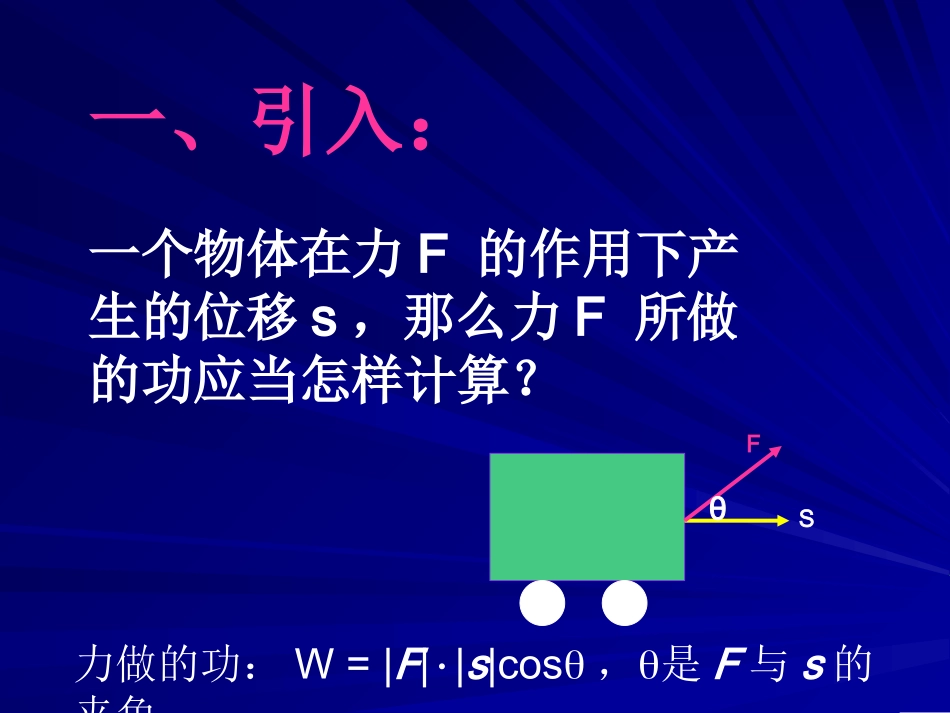
平面向量的数量积一、引入:一个物体在力F的作用下产生的位移s,那么力F所做的功应当怎样计算?SFθ力做的功:W=|F||s|cos,是F与s的夹角向量的数量积1.两个非零向量夹角的概念说明:(1)当θ=0时,a与b同向;(2)当θ=π时,a与b反向;(3)当θ=π/2时,a与b垂直,记a⊥b;(4)注意在两向量的夹角定义中,两向量必须是同起点的.范围0≤≤180baOabO已知非零向量a与b,作=a,=b,则∠AOB=θ(0≤θ≤π)叫a与b的夹角.OB�OA�平面向量数量积(内积)的定义:已知两个非零向量a与b,它们的夹角是θ,则数量|a||b|cos叫a与b的数量积,记作ab,即有ab=|a||b|cos,(0≤θ≤π).规定0与任何向量的数量积为0。探究:两个向量的数量积与向量同实数积有很大区别(1)两个向量的数量积是一个实数,不是向量,符号由cos的符号所决定。(2)两个向量的数量积称为内积,写成ab;符号“·”在向量运算中不是乘号,既不能省略,也不能用“×”代替.(3)在实数中,若a0,且ab=0,则b=0;在数量积中,若a0,且ab=0,能不能推出b=0?为什么?(4)由ab=bc能否推出a=c?(5)在实数中,有(ab)c=a(bc),但是(ab)ca(bc)显然,这是因为左端是与c共线的向量,而右端是与a共线的向量,而一般a与c不共线。3.“投影”的概念:定义:|b|cos叫做向量b在a方向上的投影。投影也是一个数量,不是向量;当为锐角时投影为正值;当为钝角时投影为负值;当为直角时投影为0;当=0时投影为|b|;当=180时投影为|b|。4.向量的数量积的几何意义:数量积ab等于a的长度与b在a方向上投影|b|cos的乘积。5.两个向量的数量积的性质:设a、b为两个非零向量,e是与b同向的单位向量。1ea=ae=|a|cos2abab=03当a与b同向时,ab=|a||b|;当a与b反向时,ab=|a||b|。特例:aa=|a|2或aaa||4cos=||||baba5|ab|≤|a||b|例1判断正误,并简要说明理由.①a·0=0;②0·a=0;③0-=;④|a·b|=|a||b|;⑤若a≠0,则对任一非零b有a·b≠0;⑥a·b=0,则a与b中至少有一个为0;⑦对任意向量a,b,с都有(a·b)с=a•(b·с);⑧a与b是两个单位向量,则a2=b2.BAAB�例2已知|a|=3,|b|=6,当①a∥b,②a⊥b,③a与b的夹角是60°时,分别求a·b.例3判断下列命题的真假:在△ABC中,若,则△ABC是锐角三角形;在△ABC中,若,则△ABC是钝角三角形;△ABC为直角三角形的充要条件是0ABBC�0ABBC�0ABBC�例3判断下列命题的真假:在△ABC中,若,则△ABC是锐角三角形;在△ABC中,若,则△ABC是钝角三角形;△ABC为直角三角形的充要条件是0ABBC�0ABBC�0ABBC�例4试证明:若四边形ABCD满足则四边形ABCD为矩形.0,0,ABCDABBC�且五、作业:习题5.61~6.《优化设计》P81强化训练1~8.例5设正三角形ABC的边长为2,,,,.ABcBCaCAbabbcca�求