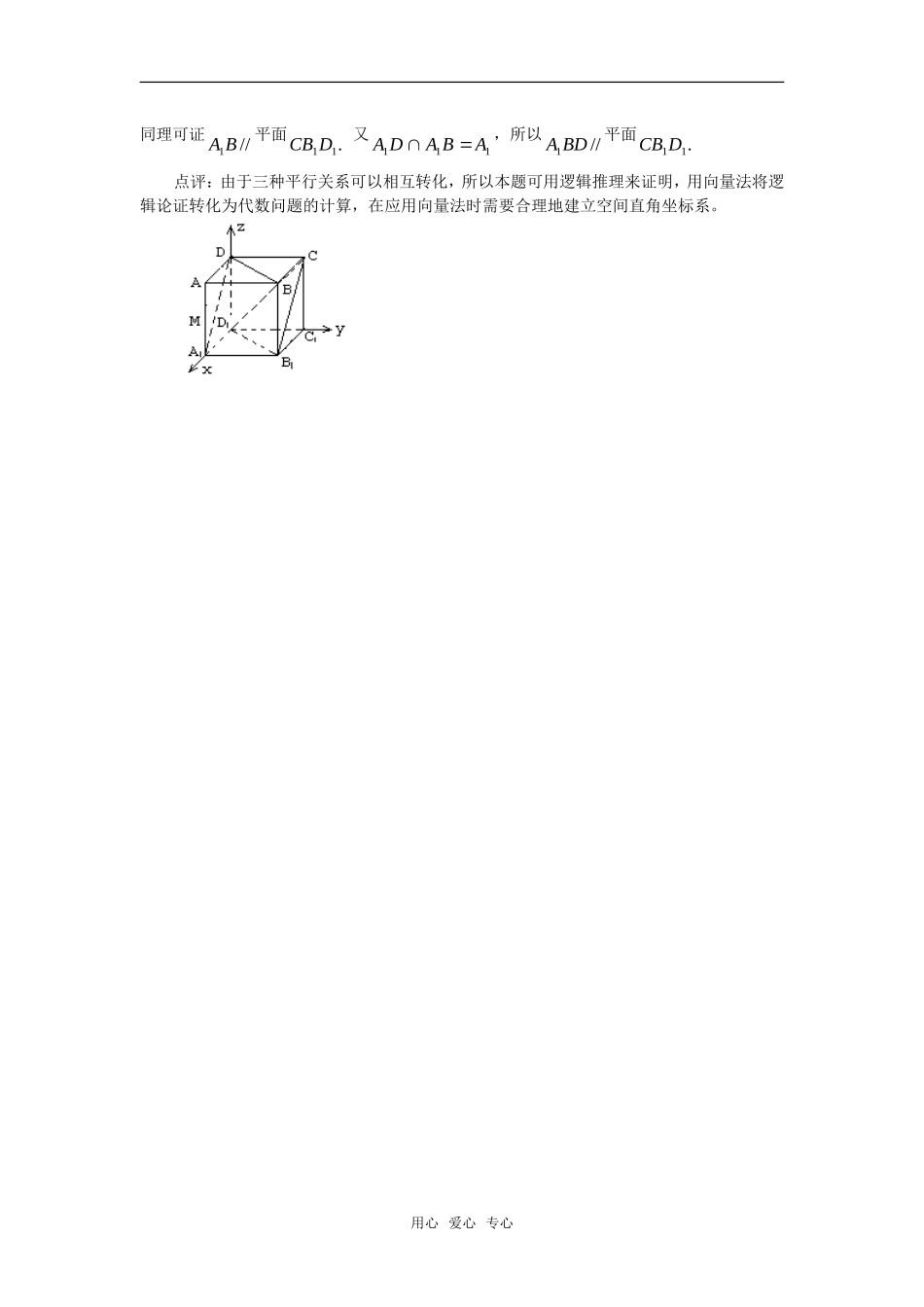
空间向量在平行中的应用向量是研究图形性质的有力工具,任何一个空间向量都可用三个不在同一平面内的向量来表示,从而使得对空间图形性质的研究代数化,以棱柱、棱锥为依托,与空间角、距离等有关的问题,可采用空间向量的知识求解。我们可以以空间不共面的(特别是过一顶点的互相垂直的)三个向量为基底,证共线、共面问题,线面平行问题。例1、已知正方体1111DCBAABCD中,点E、F、G、H、K、M分别为所有棱的中点,如图,求证:EF、GH、KM共面。分析:证EF、GH、KM共面,等价于证0KMGHEF.证明:设cBBbBFaBE2,,1,则abEFcGC,1,.,cbKMacGH所以.0)(cbacabKMGHEF所以MKHGEF,因为GH与KM不共线,所以KMGHEF,,是共面向量故EF、GH、KM共面。例2、如图,已知四边形ABCD,ABEF为两个正方形,M、N分别在其对角线BF和AC上,且FM=AN,求证:MN//平面EBC.证明:在正方形ABCD,ABEF中,因为BE=AB,FM=AN,FB=AC,所以存在实数,使.,ACANBFMF所以EBADABBABEACEBBFANFAMFMN)(.)1()()(BCBEBEBCBEEBADBE所以BCBEMN,,共面,因为M、N不在平面EBC内,所以MN//平面EBC.点评:向量p与两个不共线的向量a、b共面的充要条件是存在实数对x,y使p=xa+yb,利用共面向量定理可以证明线面平行问题。例3、正方体1111DCBAABCD中,求证://1BDA平面.11DCB证明:如图,分别以DDCDAD11111,,三边所在直线为x轴、y轴、z轴建立空间直角坐标系,设正方体的棱长为1,则)1,0,0(),1,1,0(),0,1,1(),0,0,1(11DCBA,则)1,0,1(),1,0,1(11CBDA,所以CBDA11//,即直线CBDA11//,所以//1DA平面.11DCB用心爱心专心同理可证//1BA平面.11DCB又DA111ABA,所以//1BDA平面.11DCB点评:由于三种平行关系可以相互转化,所以本题可用逻辑推理来证明,用向量法将逻辑论证转化为代数问题的计算,在应用向量法时需要合理地建立空间直角坐标系。用心爱心专心