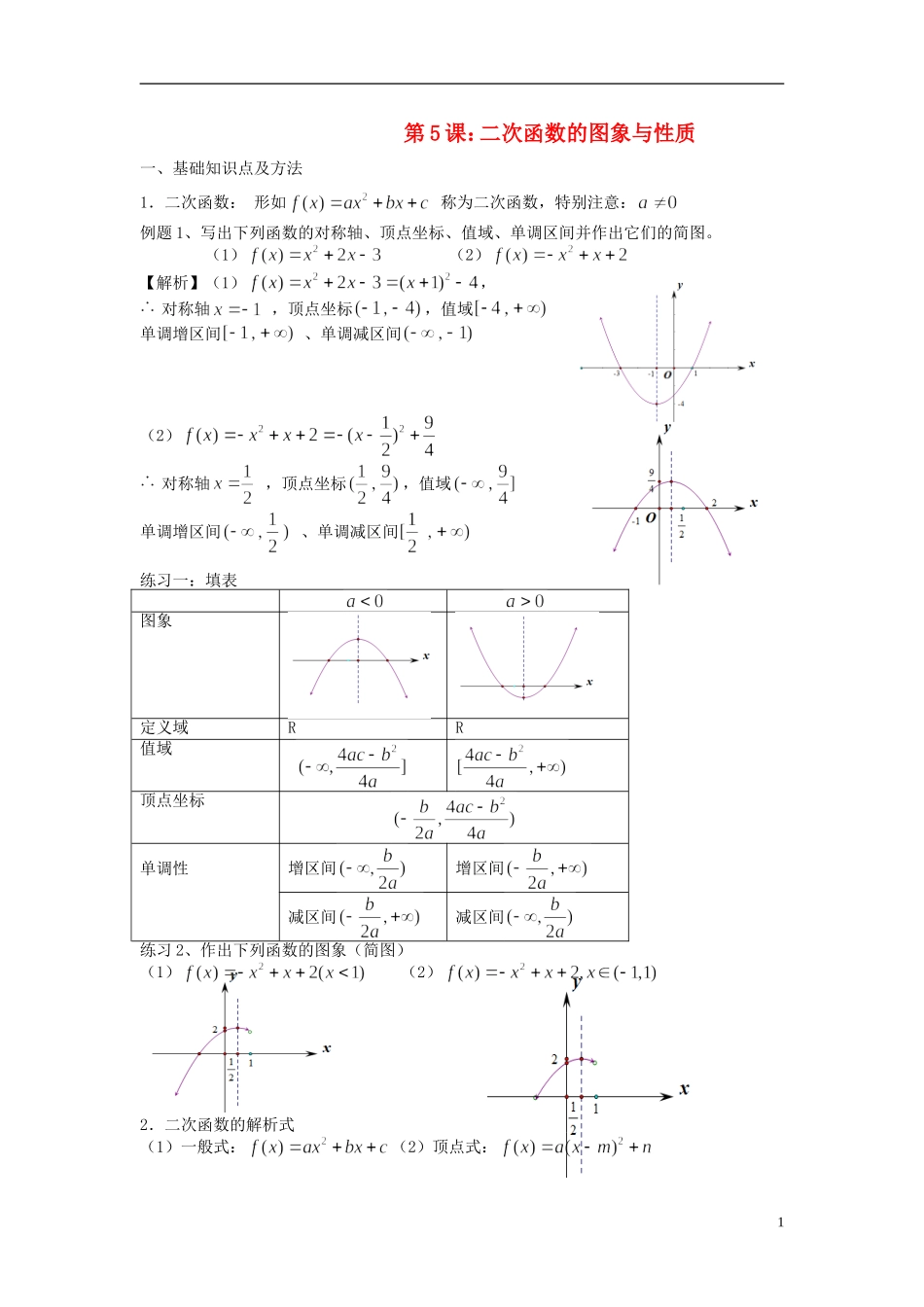
第5课:二次函数的图象与性质一、基础知识点及方法1.二次函数:形如称为二次函数,特别注意:例题1、写出下列函数的对称轴、顶点坐标、值域、单调区间并作出它们的简图。(1)(2)【解析】(1),对称轴,顶点坐标,值域单调增区间、单调减区间(2)对称轴,顶点坐标,值域单调增区间、单调减区间练习一:填表图象定义域RR值域顶点坐标单调性增区间增区间减区间减区间练习2、作出下列函数的图象(简图)(1)(2)2.二次函数的解析式(1)一般式:(2)顶点式:1(3)交点式:例题二:已知二次函数的图象过点求这个二次函数的解析式,并写出函数的值域和单调区间?【解析】设该二次函数为.由条件得.∴所求的二次函数的解析式为.值域为,递增区间为,递减区间为3.二次函数图象的对称性应用变式1:二次函数满足且的最大值为8,求此二次函数的解析式?【解析】方法1:设f(x)=ax2+bx+c(a≠0),依题意有解之,得∴所求二次函数为y=-4x2+4x+7.方法2:设f(x)=a(x-m)2+n,a≠0.∵f(2)=f(-1),∴抛物线对称轴为x==.∴m=.又根据题意函数有最大值为n=8,∴y=f(x)=a2+8.∵f(2)=-1,∴a2+8=-1,解之,得a=-4.∴f(x)=-42+8=-4x2+4x+7.变式2:二次函数满足则()ABCD无法比较的大小【答案】C【解析】∵二次函数满足,∴二次函数的对称轴为.∵,∴.加问:试比较的大小?【解析】由上面解条及图象可知,当时,;当时,4.二次函数的单调性应用例题3:如果函数在区间内是单调增函数,则的取值范围【答案】【解析】的对称轴为,所以的递增区间为在区间内是单调增函数,,的取值范围是变式:若函数在区间内是单调函数,则的取值范围2【答案】【解析】的对称轴为,所以的递增区间为,递减区间为在区间内是单调函数,,或的取值范围是第5课:二次函数的图象与性质作业题1.画出函数的图象由图象可知,的定义域为R顶点坐标为,对称轴为值域为,递增区间为2.画出函数的图象由图可知的递增区间为的递减区间为3.函数对任意的均有,那么、、的大小关系为()A.B.C.D.【答案】C4.若函数f(x)=x2+ax+c满足f(-1)=f(3),则()A.f(0)>f(2)B.f(0)