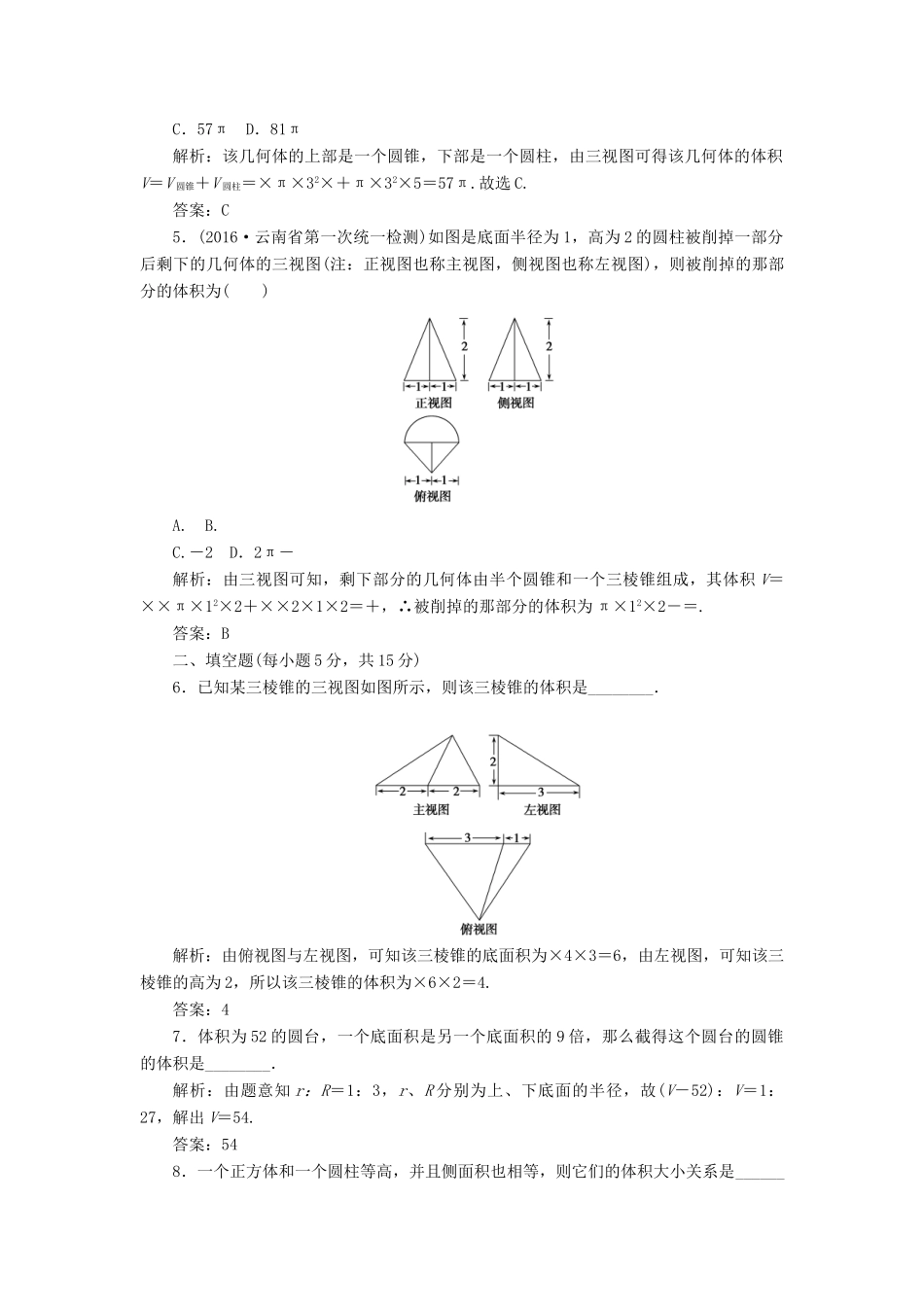
课时作业12柱、锥、台的体积|基础巩固|(25分钟,60分)一、选择题(每小题5分,共25分)1.一个长方体沿相邻三个面的对角线截去一个三棱锥,则三棱锥的体积与原来长方体体积之比为()A.1:3B.1:6C.1:8D.1:4解析:设长方体的长、宽、高分别为a,b,c,则V三棱锥=c=.又V长方体=abc.故选B.答案:B2.正四棱锥的侧棱长为2,侧棱与其在底面上的射影所成的角为60°,则该棱锥的体积为()A.3B.6C.9D.18解析:如图所示O为正四棱锥底面中心,∠PCO=60°,PC=2,则在Rt△POC中,PO=3,OC=,AC=2,AB==,∴V锥=×××3=6,故选B.答案:B3.若棱台的上、下底面面积分别为4,16,高为3,则该棱台的体积为()A.26B.28C.30D.32解析:所求棱台的体积V=×(4+16+)×3=28.答案:B4.已知某几何体的三视图如图所示,则它的体积为()A.12πB.45πC.57πD.81π解析:该几何体的上部是一个圆锥,下部是一个圆柱,由三视图可得该几何体的体积V=V圆锥+V圆柱=×π×32×+π×32×5=57π.故选C.答案:C5.(2016·云南省第一次统一检测)如图是底面半径为1,高为2的圆柱被削掉一部分后剩下的几何体的三视图(注:正视图也称主视图,侧视图也称左视图),则被削掉的那部分的体积为()A.B.C.-2D.2π-解析:由三视图可知,剩下部分的几何体由半个圆锥和一个三棱锥组成,其体积V=××π×12×2+××2×1×2=+,∴被削掉的那部分的体积为π×12×2-=.答案:B二、填空题(每小题5分,共15分)6.已知某三棱锥的三视图如图所示,则该三棱锥的体积是________.解析:由俯视图与左视图,可知该三棱锥的底面积为×4×3=6,由左视图,可知该三棱锥的高为2,所以该三棱锥的体积为×6×2=4.答案:47.体积为52的圆台,一个底面积是另一个底面积的9倍,那么截得这个圆台的圆锥的体积是________.解析:由题意知r:R=1:3,r、R分别为上、下底面的半径,故(V-52):V=1:27,解出V=54.答案:548.一个正方体和一个圆柱等高,并且侧面积也相等,则它们的体积大小关系是________.解析:设正方体棱长为a,则圆柱高为a,又设圆柱底面圆的半径为r,则4a2=2πra,即r=.∴V正方体=a3,V圆柱=πr2a=a3.∵4>π>0,∴V正方体