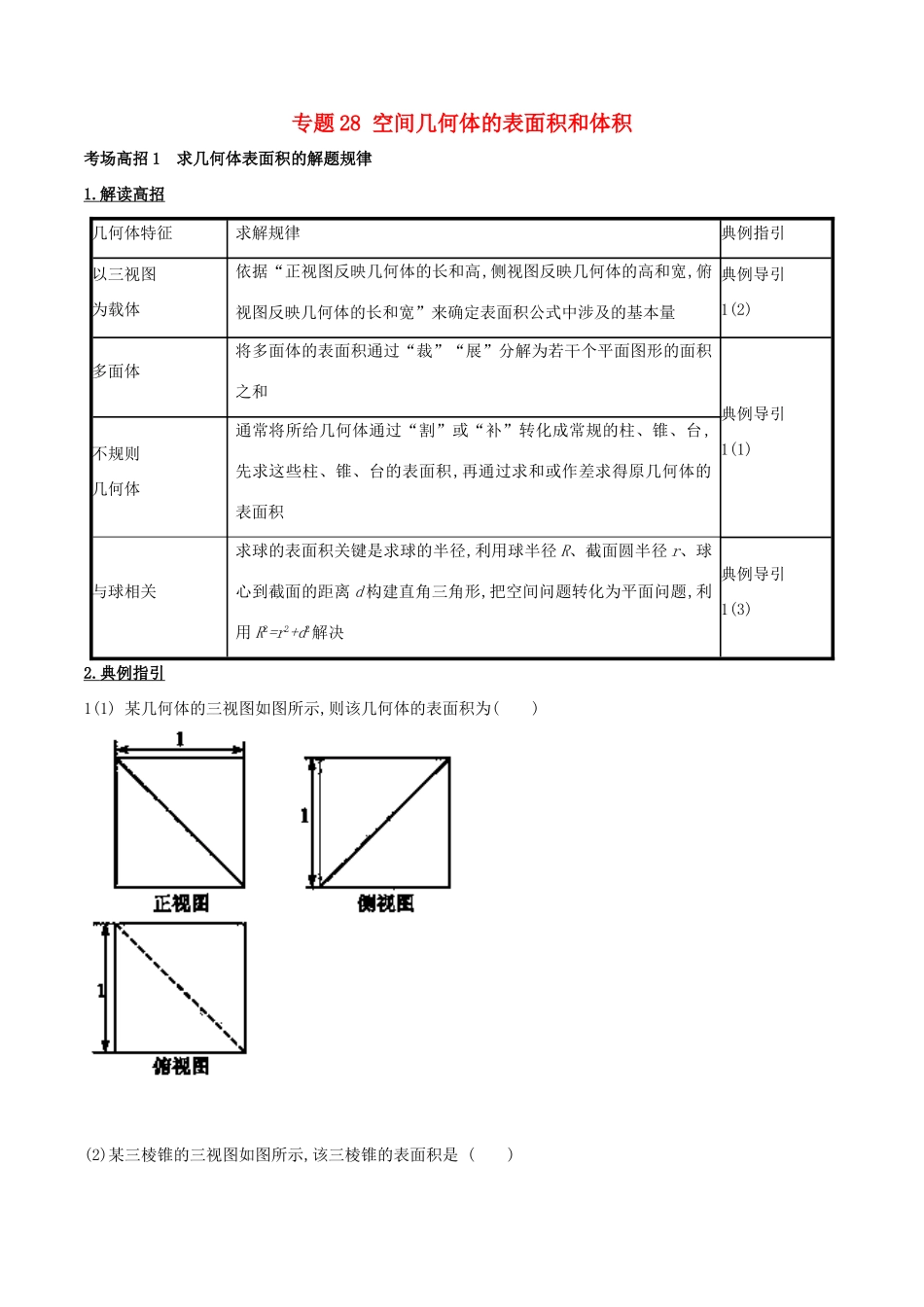
专题28空间几何体的表面积和体积考场高招1求几何体表面积的解题规律1.解读高招几何体特征求解规律典例指引以三视图为载体依据“正视图反映几何体的长和高,侧视图反映几何体的高和宽,俯视图反映几何体的长和宽”来确定表面积公式中涉及的基本量典例导引1(2)多面体将多面体的表面积通过“裁”“展”分解为若干个平面图形的面积之和典例导引1(1)不规则几何体通常将所给几何体通过“割”或“补”转化成常规的柱、锥、台,先求这些柱、锥、台的表面积,再通过求和或作差求得原几何体的表面积与球相关求球的表面积关键是求球的半径,利用球半径R、截面圆半径r、球心到截面的距离d构建直角三角形,把空间问题转化为平面问题,利用R2=r2+d2解决典例导引1(3)2.典例指引1(1)某几何体的三视图如图所示,则该几何体的表面积为()(2)某三棱锥的三视图如图所示,该三棱锥的表面积是()A.28+6B.30+6C.56+12D.60+12(3)(2017广东惠州二调)已知球O的半径为R,A,B,C三点在球O的球面上,球心O到平面ABC的距离为R,AB=AC=BC=3,则球O的表面积为.【答案】(1)D(2)B(3)16π3.亲临考场1.(2016课标Ⅰ,理6)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是()A.17πB.18πC.20πD.28π【答案】B由三视图知该几何体是平行六面体,且底面是边长为3的正方形,侧棱长为3,所以该几何体的表面积为S=2×3×6+2×3×3+2×3×3=54+18,故选B.2.(2016课标Ⅲ,理9)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()A.18+36B.54+18C.90D.81考点63几何体的体积考场高招2求几何体的体积的四大方法1.解读高招方法解读典例指引直接法对于规则几何体,直接利用公式计算即可.若已知三视图求体积,应注意三视图中的垂直关系在几何体中的位置,确定几何体中的线面垂直等关系,进而利用公式求解典例导引2(3)解法一割补法对于不规则几何体,常通过分割或者补形的手段将此几何体变为一个或几个规则的、体积易求的几何体,然后再计算.常见的有将三棱锥还原为三棱柱或长方体,将三棱柱还原为平行六面体,将台体还原为锥体等典例导引2(1)转化法经常是转换底面与高,将原来不易求解面积的底面转换为容易求面积的底面,或将原来不易看出的高转换为易看出并易求解的高.常用的转化方法有平行转移和比例转移,应根据试题的特点灵活选择典例导引2(2)等积利用三棱锥的“等积性”可以把任何一个面作为三棱锥的底面.(1)求体积时,可选择容易计算的底面和高来求解;(2)利用“等积性”可求“点典例导引2(3)法到面的距离”,方法是在面中选取三个点,与已知点构成三棱锥后进行求解解法二2.典例指引2(1)(2017河南九校质量考评)在直三棱柱ABC-A1B1C1中,M,N分别为棱A1B1,A1C1的中点,则平面BMNC将三棱柱分成的两部分的体积比为()A.8∶7B.8∶5C.7∶5D.7∶4(2)(2017河北唐山模拟)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,BC=2AD=4,AB=CD,∠ABC=60°,N为线段PC上一点,CN=3NP,M为AD的中点.①证明:MN∥平面PAB;②求点N到平面PAB的距离.(3)(2017广东汕头期末统考)如图,正四面体SABC的侧面积为48,O为底面正三角形ABC的中心.①求证:SA⊥BC;②求点O到侧面SBC的距离.(1)【解析】设直三棱柱ABC-A1B1C1的高为h,底面积为4S,则×h×3S+=hS+=hS+=hS+h·4S=Sh,所以两部分的体积比为Sh=7∶5,故选C. CN=3NP,∴点N到平面PAB的距离d=AC=.(3)①【证明】如图所示,D为BC的中点,连接AD,SD, △ABC是等边三角形,D是BC的中点,∴AD⊥BC. △SBC是等边三角形,D是BC的中点,∴SD⊥BC. AD∩SD=D,AD,SD⊂平面SAD,∴BC⊥平面SAD. SA⊂平面SAD,∴SA⊥BC.连接SO,则在Rt△SAO中,SO=a.由OD·SO=SD·OE,得a×a=a·OE,∴OE=a=,即点O到侧面SBC的距离为.∴在Rt△SAO中,SO=a=. S△OBC=·BC·OD=×8×,∴VS-OBC=·S△OBC·SO=. S△SBC=×48=16,设点O到侧面SBC的距离为h,∴由VS-OBC=VO-SBC,得·S△SBC·h,∴h=,即点O到侧面SBC的距离为.3.亲临考场1.(2017课标Ⅱ,理4)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A.90B.63πC.42πD.36π【答案】B由...