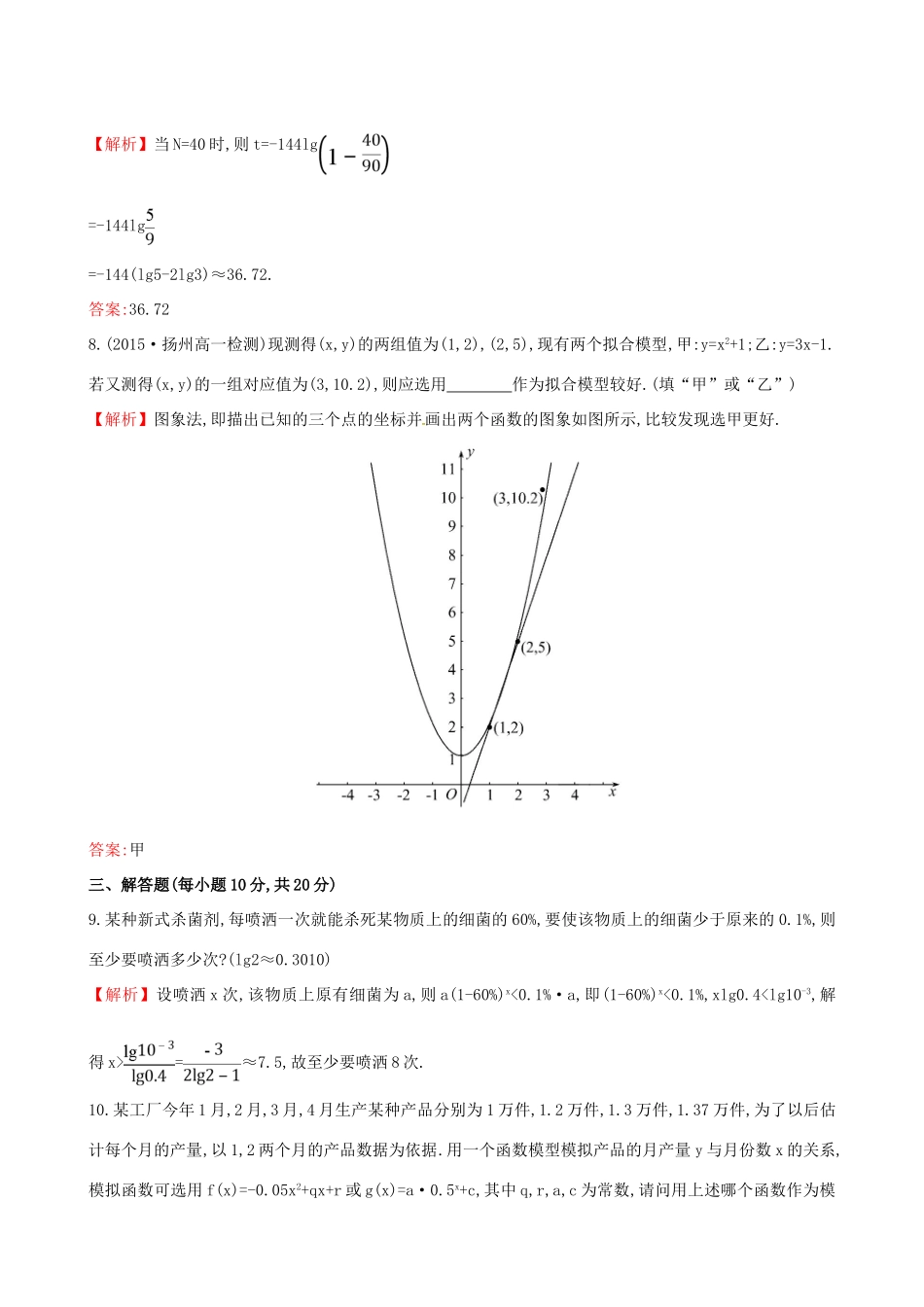
课时提升作业(二十七)指数型、对数型函数模型的应用举例(25分钟60分)一、选择题(每小题5分,共25分)1.某林场计划第一年造林10000亩,以后每年比前一年多造林20%,则第四年造林()A.14400亩B.172800亩C.17280亩D.20736亩【解析】选C.设第x年造林y亩,则y=10000(1+20%)x-1,所以x=4时,y=10000×1.23=17280(亩).2.(2015·四平高一检测)某化工厂2014年的12月份的产量是1月份产量的n倍,则该化工厂这一年的月平均增长率是()A.B.C.-1D.-1【解析】选D.设月平均增长率为x,第一个月的产量为a,则有a(1+x)11=na,所以1+x=,所以x=-1.3.(2015·长沙高一检测)在一次教学实验中,运用图形计算器采集到如下一组数据:x-2.00-1.0001.002.003.00y0.240.5112.023.988.02则x,y的函数关系与下列各类函数中最接近的是(其中a,b为待定系数)()A.y=a+B.y=a+bxC.y=a+logbxD.y=a·bx【解析】选D.因为f(0)=1,所以A.y=a+,C.y=a+logbx不符合题意.先求y=a+bx,由得所以y=1+1.02x,当x=-2时,1+1.02×(-2)=-1.04,不满足题意,选项B错误.下面求y=a·bx,由得所以y=2.02x,满足题意,选项D正确.4.某地区植被被破坏,土地沙漠化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则沙漠增加数y(万公顷)关于年数x的函数关系较为近似的是()A.y=0.2xB.y=C.y=D.y=0.2+log16x【解题指南】利用所给函数,分别令x=1,2,3,计算相应的函数值,即可求得结论.【解析】选C.对于A,x=1,2时,符合题意,x=3时,y=0.6,与0.76相差0.16;对于B,x=1时,y=0.3;x=2时,y=0.8;x=3时,y=1.5,相差较大,不符合题意;对于C,x=1,2时,符合题意,x=3时,y=0.8,与0.76相差0.04,与A比较,更符合题意;对于D,x=1时,y=0.2;x=2时,y=0.45;x=3时,y<0.6,相差较大,不符合题意.5.某种植物生长发育的数量y与时间x的关系如表:x123…y138…则下面的函数关系式中,能表达这种关系的是()A.y=2x-1B.y=x2-1C.y=2x-1D.y=1.5x2-2.5x+2【解析】选D.画散点图或代入数值,选择拟合效果最好的函数,可知应选D.二、填空题(每小题5分,共15分)6.(2015·镇江高一检测)某细菌在培养过程中,每15分钟分裂一次(由一个分裂成两个),则这种细菌由一个繁殖成4096个需要经过小时.【解析】设共分裂了x次,则有2x=4096,即2x=212,所以x=12.所用的时间为15分钟×12=180分钟=3小时.答案:37.“学习曲线”可以用来描述学习某一任务的速度,假设函数t=-144lg中,t表示达到某一英文打字水平所需的学习时间,N表示每分钟打出的字数.则当N=40时,t=.(已知lg5≈0.699,lg3≈0.477)【解析】当N=40时,则t=-144lg=-144lg=-144(lg5-2lg3)≈36.72.答案:36.728.(2015·扬州高一检测)现测得(x,y)的两组值为(1,2),(2,5),现有两个拟合模型,甲:y=x2+1;乙:y=3x-1.若又测得(x,y)的一组对应值为(3,10.2),则应选用作为拟合模型较好.(填“甲”或“乙”)【解析】图象法,即描出已知的三个点的坐标并画出两个函数的图象如图所示,比较发现选甲更好.答案:甲三、解答题(每小题10分,共20分)9.某种新式杀菌剂,每喷洒一次就能杀死某物质上的细菌的60%,要使该物质上的细菌少于原来的0.1%,则至少要喷洒多少次?(lg2≈0.3010)【解析】设喷洒x次,该物质上原有细菌为a,则a(1-60%)x<0.1%·a,即(1-60%)x<0.1%,xlg0.4=≈7.5,故至少要喷洒8次.10.某工厂今年1月,2月,3月,4月生产某种产品分别为1万件,1.2万件,1.3万件,1.37万件,为了以后估计每个月的产量,以1,2两个月的产品数据为依据.用一个函数模型模拟产品的月产量y与月份数x的关系,模拟函数可选用f(x)=-0.05x2+qx+r或g(x)=a·0.5x+c,其中q,r,a,c为常数,请问用上述哪个函数作为模拟函数较好?说明理由.【解析】用g(x)=a·0.5x+c作为模拟函数较好,理由如下:f(x)=-0.05x2+qx+r由f(1)=1,f(2)=1.2得q=0.35,r=0.7,f(3)=1.3,f(4)=1.3;而对于g(x)=a·0.5x+c,由g(1)=1,g(2)=1.2,得a=-0.8,c=1.4,g(3)=1.3,g(4)=1.35,所以用g(x)=a·0.5x+c作为模拟函数较好.【拓展延伸】函数建模的基本思想(20分钟40分)一、选择题(每小题5分,共10分)1.(2015·舟山高一检测)若镭经过100年后剩留原来质量的95.76%,设质量为1的镭经过x年后剩留量为y,则x,y的函数关系是()A.y=B.y=C.y=D.y=1-(0.0424【解析】选A.设镭一年放射掉...