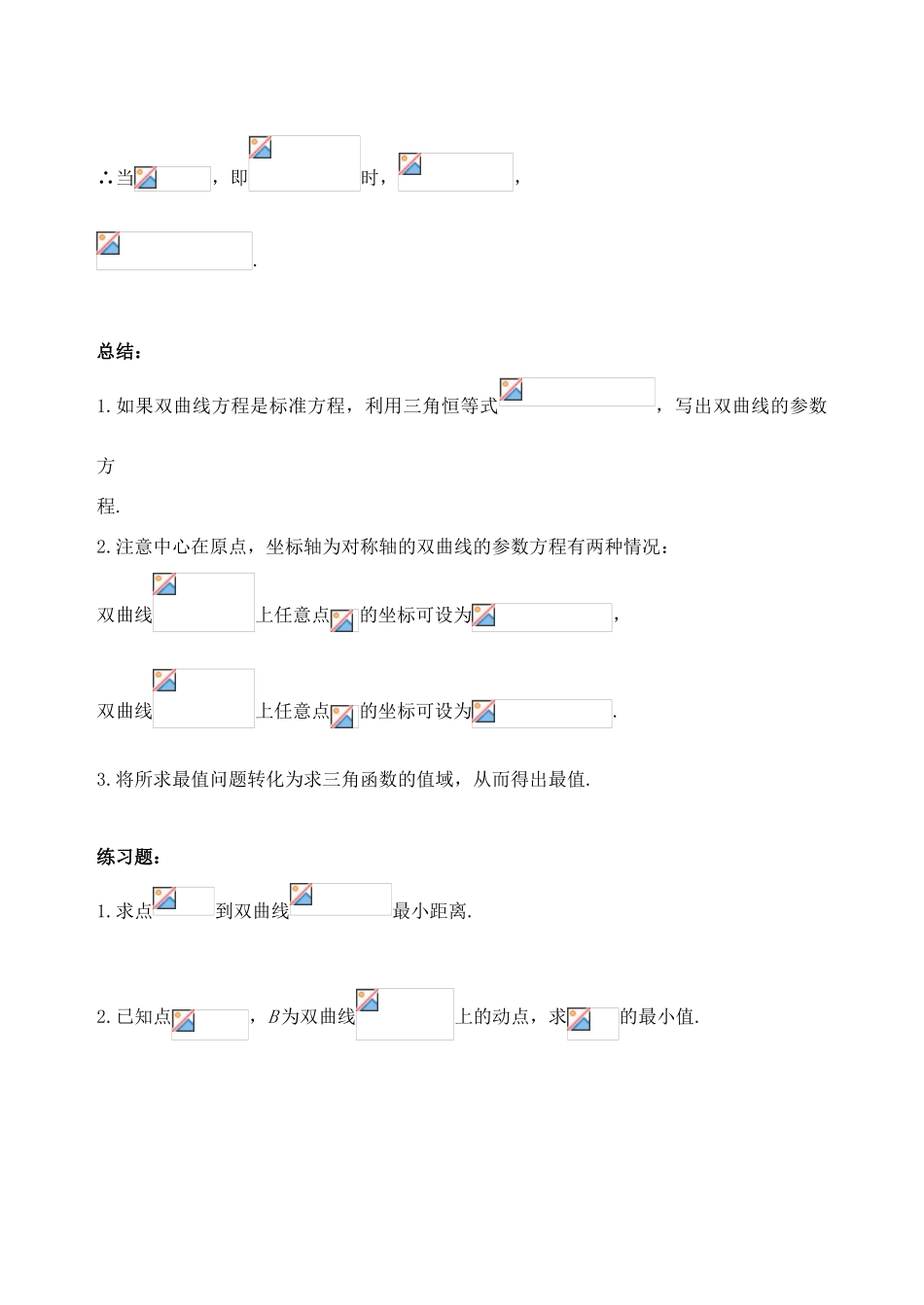
二利用双曲线的参数方程求最值今天我们研究利用双曲线的参数方程求最值.已知双曲线的标准方程,则可以将双曲线的方程改写成参数方程,于是双曲线上的点的坐标写成参数形式,把所求问题转化为三角函数问题.通过例题来看.例1:已知在双曲线上,求到点的距离的最小值.有最小值为.注意:1.中心在原点,坐标轴为对称轴的双曲线的参数方程有以下两种情况:焦点在轴上的双曲线:(θ为参数).焦点在轴上的双曲线:(θ为参数).以上的,且.2.θ称为双曲线的离心角,注意离心角的几何意义.3.双曲线上任意点的坐标可设为.4.注意:.例2:已知圆O:上一点P与双曲线上一点Q,求P,Q两点距离的最小值.解:设双曲线上点的坐标为,先求圆心到双曲线上点的最小距离:,∴当,即时,,.总结:1.如果双曲线方程是标准方程,利用三角恒等式,写出双曲线的参数方程.2.注意中心在原点,坐标轴为对称轴的双曲线的参数方程有两种情况:双曲线上任意点的坐标可设为,双曲线上任意点的坐标可设为.3.将所求最值问题转化为求三角函数的值域,从而得出最值.练习题:1.求点到双曲线最小距离.2.已知点,B为双曲线上的动点,求的最小值.3.已知双曲线C:,P是C上的任意点.(Ⅰ)求证:点P到双曲线C的两条渐近线的距离的乘积是一个常数;(Ⅱ)设点A的坐标为(3,0),求|PA|的最小值.练习题解析:1.求点到双曲线最小距离.令,整理得,所以,所以,解得,所以.所以点到双曲线最小距离是.2.已知点,B为双曲线上的动点,求的最小值.解:设双曲线上点的坐标为,,∴当,即时,.3.已知双曲线C:,P是C上的任意点.(Ⅰ)求证:点P到双曲线C的两条渐近线的距离的乘积是一个常数;(Ⅱ)设点A的坐标为(3,0),求|PA|的最小值.