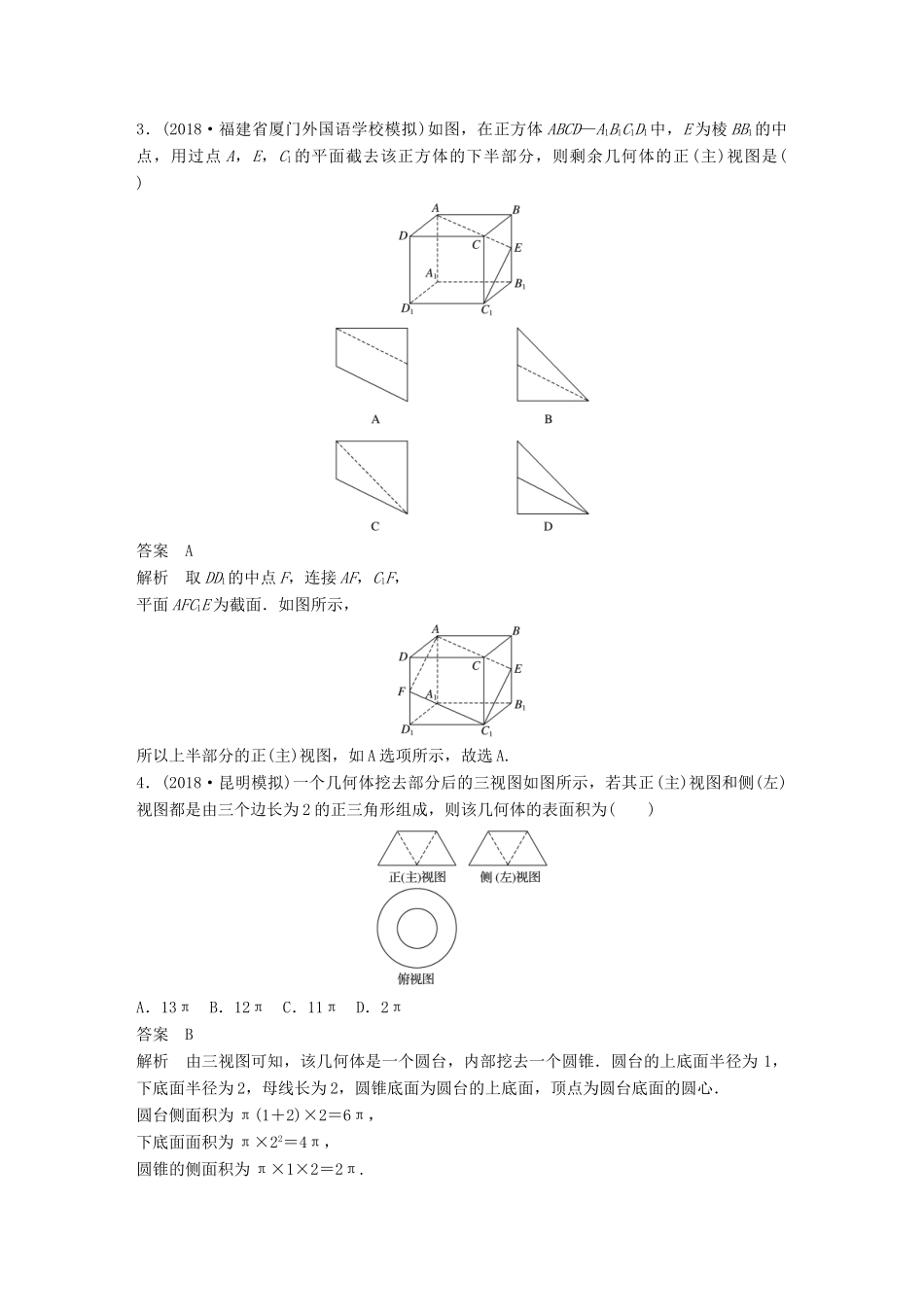
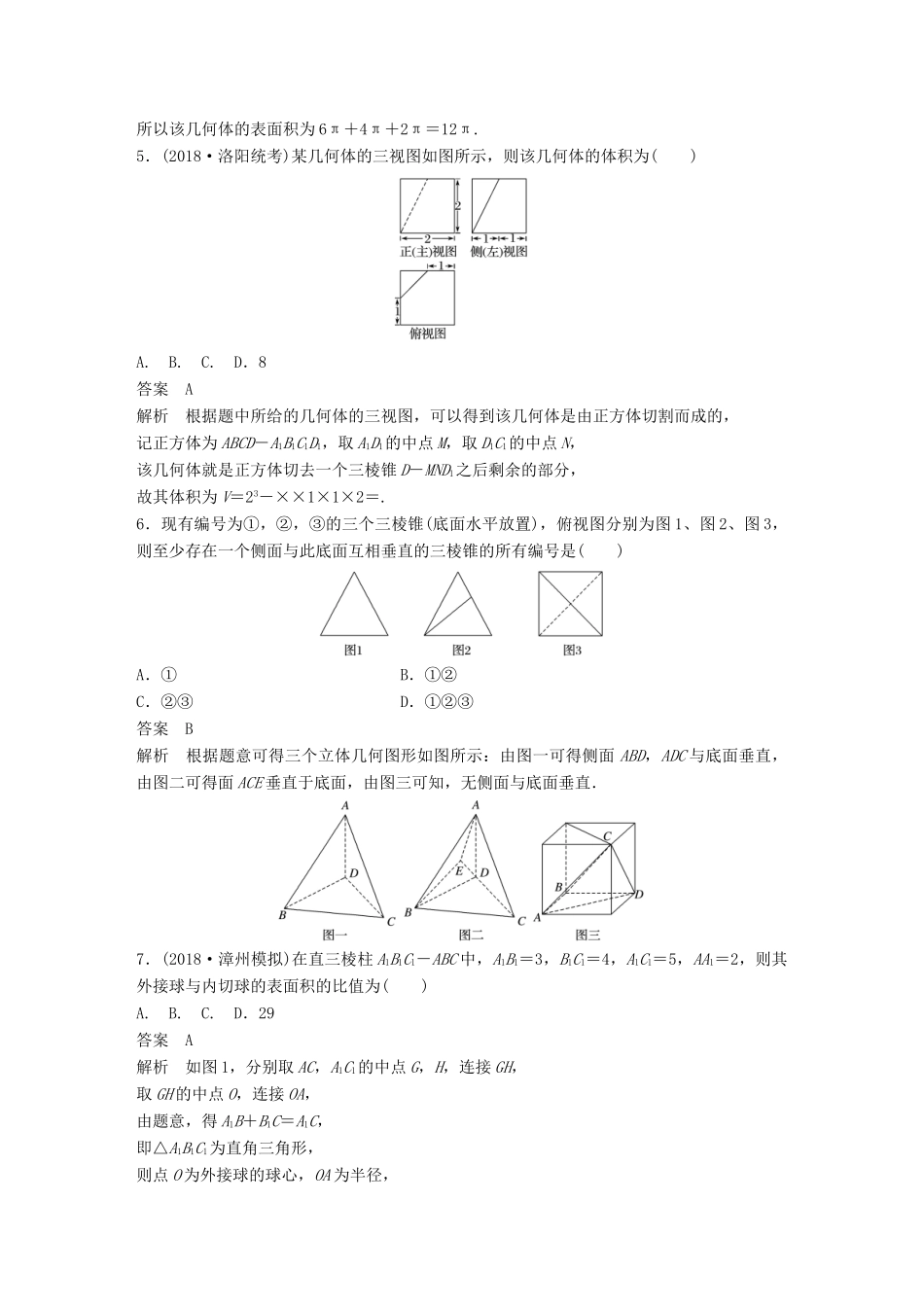
12+4分项练9立体几何1.已知a,b为异面直线,下列结论不正确的是()A.必存在平面α,使得a∥α,b∥αB.必存在平面α,使得a,b与α所成角相等C.必存在平面α,使得a⊂α,b⊥αD.必存在平面α,使得a,b与α的距离相等答案C解析由a,b为异面直线知,在A中,在空间中任取一点O(不在a,b上),过点O分别作a,b的平行线,则由过点O的a,b的平行线确定一个平面α,使得a∥α,b∥α,故A正确;在B中,平移b至b′与a相交,因而确定一个平面α,在α上作a,b′夹角的平分线,明显可以作出两条.过角平分线且与平面α垂直的平面使得a,b′与该平面所成角相等,角平分线有两条,所以有两个平面都可以.故B正确;在C中,当a,b不垂直时,不存在平面α,使得a⊂α,b⊥α,故C错误;在D中,过异面直线a,b的公垂线的中点作与公垂线垂直的平面α,则平面α使得a,b与α的距离相等,故D正确.故选C.2.(2018·泸州模拟)设a,b是空间中不同的直线,α,β是不同的平面,则下列说法正确的是()A.a∥b,b⊂α,则a∥αB.a⊂α,b⊂β,α∥β,则a∥bC.a⊂α,b⊂α,a∥β,b∥β,则α∥βD.α∥β,a⊂α,则a∥β答案D解析由a,b是空间中不同的直线,α,β是不同的平面知,在A中,a∥b,b⊂α,则a∥α或a⊂α,故A错误;在B中,a⊂α,b⊂β,α∥β,则a与b平行或异面,故B错误;在C中,a⊂α,b⊂α,a∥β,b∥β,则α与β相交或平行,故C错误;在D中,α∥β,a⊂α,则由面面平行的性质得a∥β,故D正确.3.(2018·福建省厦门外国语学校模拟)如图,在正方体ABCD—A1B1C1D1中,E为棱BB1的中点,用过点A,E,C1的平面截去该正方体的下半部分,则剩余几何体的正(主)视图是()答案A解析取DD1的中点F,连接AF,C1F,平面AFC1E为截面.如图所示,所以上半部分的正(主)视图,如A选项所示,故选A.4.(2018·昆明模拟)一个几何体挖去部分后的三视图如图所示,若其正(主)视图和侧(左)视图都是由三个边长为2的正三角形组成,则该几何体的表面积为()A.13πB.12πC.11πD.2π答案B解析由三视图可知,该几何体是一个圆台,内部挖去一个圆锥.圆台的上底面半径为1,下底面半径为2,母线长为2,圆锥底面为圆台的上底面,顶点为圆台底面的圆心.圆台侧面积为π(1+2)×2=6π,下底面面积为π×22=4π,圆锥的侧面积为π×1×2=2π.所以该几何体的表面积为6π+4π+2π=12π.5.(2018·洛阳统考)某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.8答案A解析根据题中所给的几何体的三视图,可以得到该几何体是由正方体切割而成的,记正方体为ABCD-A1B1C1D1,取A1D1的中点M,取D1C1的中点N,该几何体就是正方体切去一个三棱锥D-MND1之后剩余的部分,故其体积为V=23-××1×1×2=.6.现有编号为①,②,③的三个三棱锥(底面水平放置),俯视图分别为图1、图2、图3,则至少存在一个侧面与此底面互相垂直的三棱锥的所有编号是()A.①B.①②C.②③D.①②③答案B解析根据题意可得三个立体几何图形如图所示:由图一可得侧面ABD,ADC与底面垂直,由图二可得面ACE垂直于底面,由图三可知,无侧面与底面垂直.7.(2018·漳州模拟)在直三棱柱A1B1C1-ABC中,A1B1=3,B1C1=4,A1C1=5,AA1=2,则其外接球与内切球的表面积的比值为()A.B.C.D.29答案A解析如图1,分别取AC,A1C1的中点G,H,连接GH,取GH的中点O,连接OA,由题意,得A1B+B1C=A1C,即△A1B1C1为直角三角形,则点O为外接球的球心,OA为半径,则R=OA==;如图2,作三棱柱的中截面,则中截面三角形的内心是该三棱柱的内切球的球心,中截面三角形的内切圆的半径r==1,也是内切球的半径,因为R∶r=∶2,则其外接球与内切球的表面积的比值为=.8.(2018·南昌模拟)已知E,F,H,G分别是四面体ABCD棱AB,BC,CD,DA上的点,且AE=EB,BF=FC,CH=2HD,AG=2GD,则下列说法错误的是()A.AC∥平面EFHB.BD∥平面EFGC.直线EG,FH,BD相交于同一点D.FE∥GH答案B解析对于A,EA=EB,BF=FC,CH=2HD,AG=2GD,可得到GH∥AC,EF∥AC,又AC⊄平面EFH,故AC∥平面EFH,选项A正确.对于B,因为BD和FH不平行,而且两条直线在...