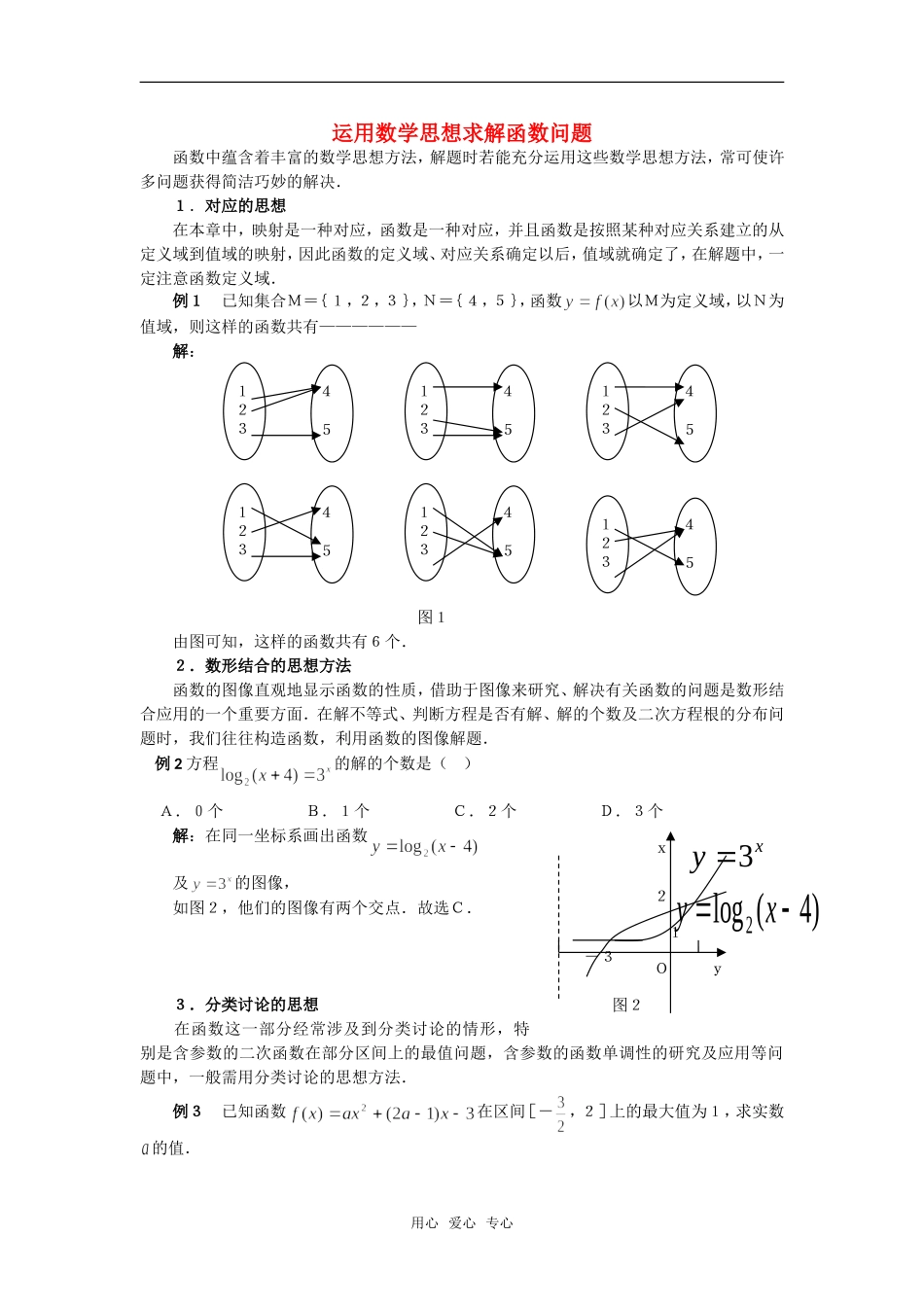
123451234512345123451234512345Oxy-321)4(log2xyxy3图2运用数学思想求解函数问题函数中蕴含着丰富的数学思想方法,解题时若能充分运用这些数学思想方法,常可使许多问题获得简洁巧妙的解决.1.对应的思想在本章中,映射是一种对应,函数是一种对应,并且函数是按照某种对应关系建立的从定义域到值域的映射,因此函数的定义域、对应关系确定以后,值域就确定了,在解题中,一定注意函数定义域.例1已知集合M={1,2,3},N={4,5},函数以M为定义域,以N为值域,则这样的函数共有——————解:图1由图可知,这样的函数共有6个.2.数形结合的思想方法函数的图像直观地显示函数的性质,借助于图像来研究、解决有关函数的问题是数形结合应用的一个重要方面.在解不等式、判断方程是否有解、解的个数及二次方程根的分布问题时,我们往往构造函数,利用函数的图像解题.例2方程的解的个数是()A.0个B.1个C.2个D.3个解:在同一坐标系画出函数及的图像,如图2,他们的图像有两个交点.故选C.3.分类讨论的思想在函数这一部分经常涉及到分类讨论的情形,特别是含参数的二次函数在部分区间上的最值问题,含参数的函数单调性的研究及应用等问题中,一般需用分类讨论的思想方法.例3已知函数在区间[-,2]上的最大值为1,求实数的值.用心爱心专心解:=0时,=--3,在[-,2]上不能取得1,故0.(0)的对称轴方程为(1)令,解得=-,此时[-,2]∵<0,最大,所以不合适.(2)令,解得=,此时[-,2]∵=>0,∴最大,合适.(3)令=1,解得=,验证后知只有=才合适.综上所述,=,或=.4.转化与化归的思想在解决恒成立及复合函数等问题时,往往可以把问题转化为指数函数、对数函数、二次函数、幂函数等我们熟悉的函数去研究,将复杂的问题分解、归结为简单问题.例4已知函数,,若对任意,>0恒成立,试求实数的取值范围.解:在区间[1,+)上,>0恒成立恒成立.设,∵=递增,∴当=1时,,当且仅当>0时,函数>0恒成立.故>-35.函数与方程的思想本章中学习了指数函数、对数函数,研究了分段函数,函数的定义域、值域、单调性、奇偶性、对称性.因此,用函数和方程的观点指导解题,是一种重要思想方法.例5设,且它们的绝对值都不大于1,求证:.分析:构造函数,是关于的一次函数,由于[-1,1],只要证明且,就能证明.证明:设,是关于的一次函数∵∴∴在[-1,1]上恒为负,∴.评注:本题解法的关键在于要具有函数意识,能结合式子的特征构造出一次函数,从而由一次函数的图像性质,使问题得以解决.用心爱心专心用心爱心专心