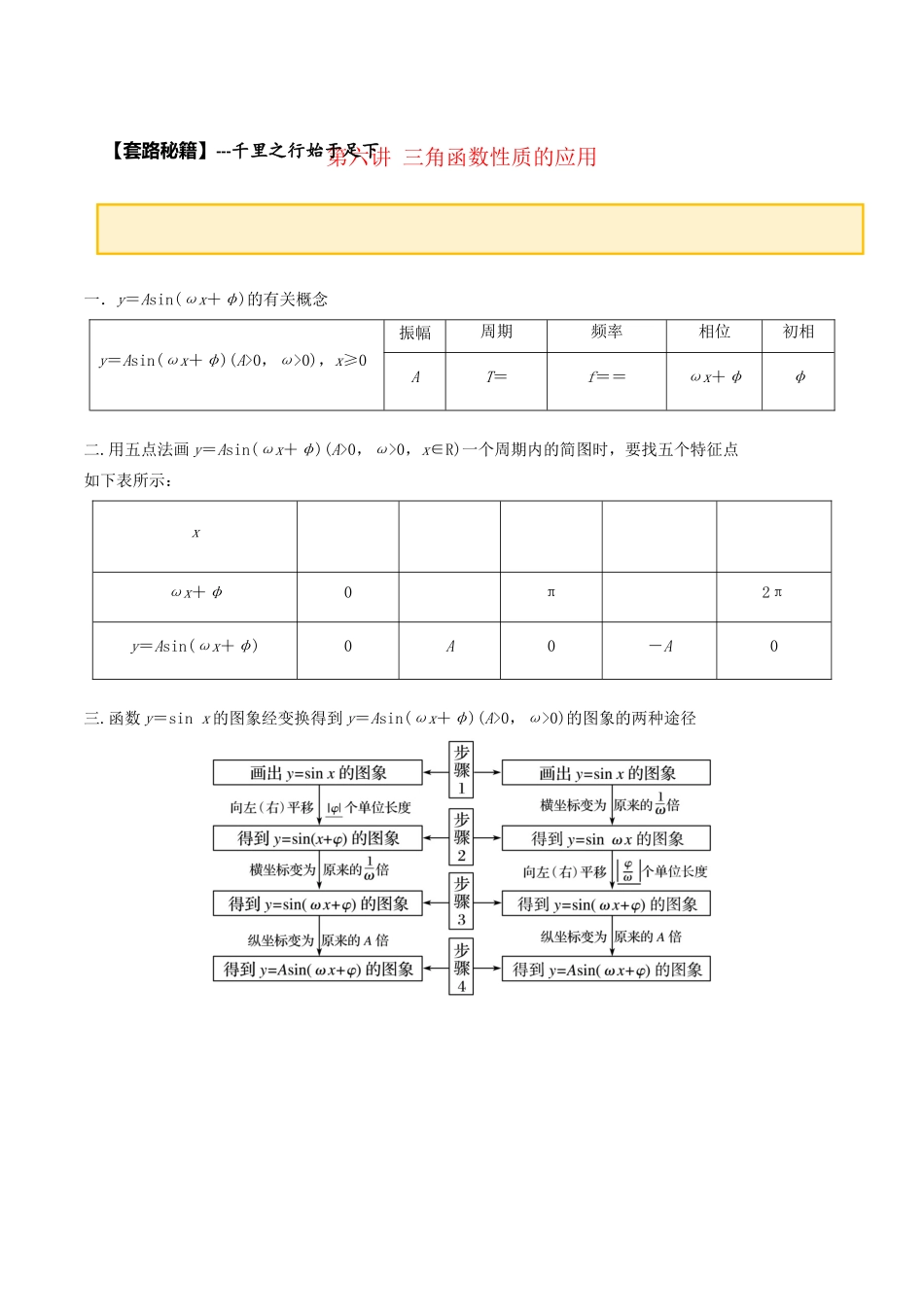
第六讲三角函数性质的应用一.y=Asin(ωx+φ)的有关概念y=Asin(ωx+φ)(A>0,ω>0),x≥0振幅周期频率相位初相AT=f==ωx+φφ二.用五点法画y=Asin(ωx+φ)(A>0,ω>0,x∈R)一个周期内的简图时,要找五个特征点如下表所示:xωx+φ0π2πy=Asin(ωx+φ)0A0-A0三.函数y=sinx的图象经变换得到y=Asin(ωx+φ)(A>0,ω>0)的图象的两种途径【套路秘籍】---千里之行始于足下【修炼套路】---为君聊赋《今日诗》,努力请从今日始考向一求解析式【例1】(1)函数f(x)=Asin(ωx+)(A>0,ω>0,||<π)的部分图象如图所示,则函数f(x)的解析式为.(2)已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<π2,则()A.A=4B.ω=1C.φ=π6D.B=4【答案】(1)f(x)=sin(2x+)(2)C【解析】(1)由图可知A=,=-=,所以T=π,故ω=2,因此f(x)=sin(2x+).又函数图象过点(,0)因此2×+=π+2kπ,k∈Z,又根据||<π,所以=,故f(x)=sin(2x+).(2)如图根据函数的最大值和最小值得¿求得A=2,B=2函数的周期为(5π12−π6)×4=π,即π=2πω,ω=2当x=π6时取最大值,即sin(2×π6+φ)=1,2×π6+φ=2kπ+π2 |φ|<π2∴φ=π6故选:C.【套路总结】由y=Asin(ωx+φ)的图象确定解析式的方法(1)第一零点法:如果从图象可直接确定A和ω,则选取“第一零点”(即“五点法”作图中的第一个点)的数据代入“ωx+φ=0”(要注意正确判断哪一点是“第一零点”)求得φ.(2)特殊值法:通过若干特殊点代入函数式,可以求得相关待定系数A,ω,φ.这里需要注意的是,要认清所选择的点属于五个点中的哪一点,并能正确代入列式.(3)图象变换法:运用逆向思维的方法,先确定函数的基本解析式y=Asinωx,再根据图象平移规律确定相关的参数.【举一反三】1.函数y=Asin(ωx+φ)的部分图象如图所示,则()A.y=2sinB.y=2sinC.y=2sinD.y=2sin【答案】A【解析】由图可知,A=2,最小正周期T=π,所以ω==2,所以y=2sin(2x+φ)。又因为图象过点,所以2sin=2,即+φ=2kπ+(k∈Z),当k=0时,得φ=-,所以y=2sin。2.已知函数f(x)=Atan(ωx+φ)的部分图象如图所示,则f=________.【答案】【解析】由题干图象知=2×=,所以ω=2.因为2×+φ=kπ+(k∈Z),所以φ=kπ+(k∈Z),又|φ|<,所以φ=,这时f(x)=Atan.又函数图象过点(0,1),代入上式得A=1,所以f(x)=tan.所以f=tan=.3.已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的部分图象如图所示,则函数f(4x)图象的对称中心为__________.【答案】(kπ3,1),k∈Z【解析】由题意,根据函数的图象可知A+B=3,且−A+B=−1,得A=2,B=1,则f(x)=2sin(ωx+φ)+1,又由T2=2π−2π3=4π3,即T=8π3,又由2πw=8π3,得w=34,由五点对应法得2π3×34+φ=π2,得φ=0,即f(x)=2sin(34x)+1,则f(4x)=2sin(34×4)+1=2sin(3x)+1,令3x=kπ,得x=kπ3,即函数的对称中心为(kπ3,1),k∈Z,故答案为:(kπ3,1),k∈Z.4.若直线x=π和x=π是函数y=cos(ωx+φ)(ω>0)图象的两条相邻对称轴,则φ=______________.【答案】kπ-π,k∈Z【解析】由题意,函数的周期T=2×=2π,∴ω==1,∴y=cos(x+φ),当x=π时,函数取得最大值或最小值,即cos=±1,可得π+φ=kπ,k∈Z,∴φ=kπ-π,k∈Z.考向二伸缩平移【例2】(1)要得到函数y=❑√3cos2x+sinxcosx−❑√32的图象,只需将函数y=sin2x的图象()A.向左平移π12个单位B.向右平移π12个单位C.向左平移π6个单位D.向右平移π6个单位(2)要得到函数y=❑√2cosx的图象,只需将y=❑√2cos(2x+π4)的图象所有点()A.横坐标伸长到原来的2倍,纵坐标不变,再向右平移π4个单位长度B.横坐标伸长到原来的2倍,纵坐标不变,再向右平移π8个单位长度C.横坐标缩短到原来的12倍,纵坐标不变,再向右平移π4个单位长度D.横坐标缩短到原来的12倍,纵坐标不变,再向左平移π8个单位长度(3)若函数f(x)=cos,为了得到函数g(x)=sin2x的图象,则只需将f(x)的图象()A.向右平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向左平移个单位长度【答案】(1)C(2)A(3)A...