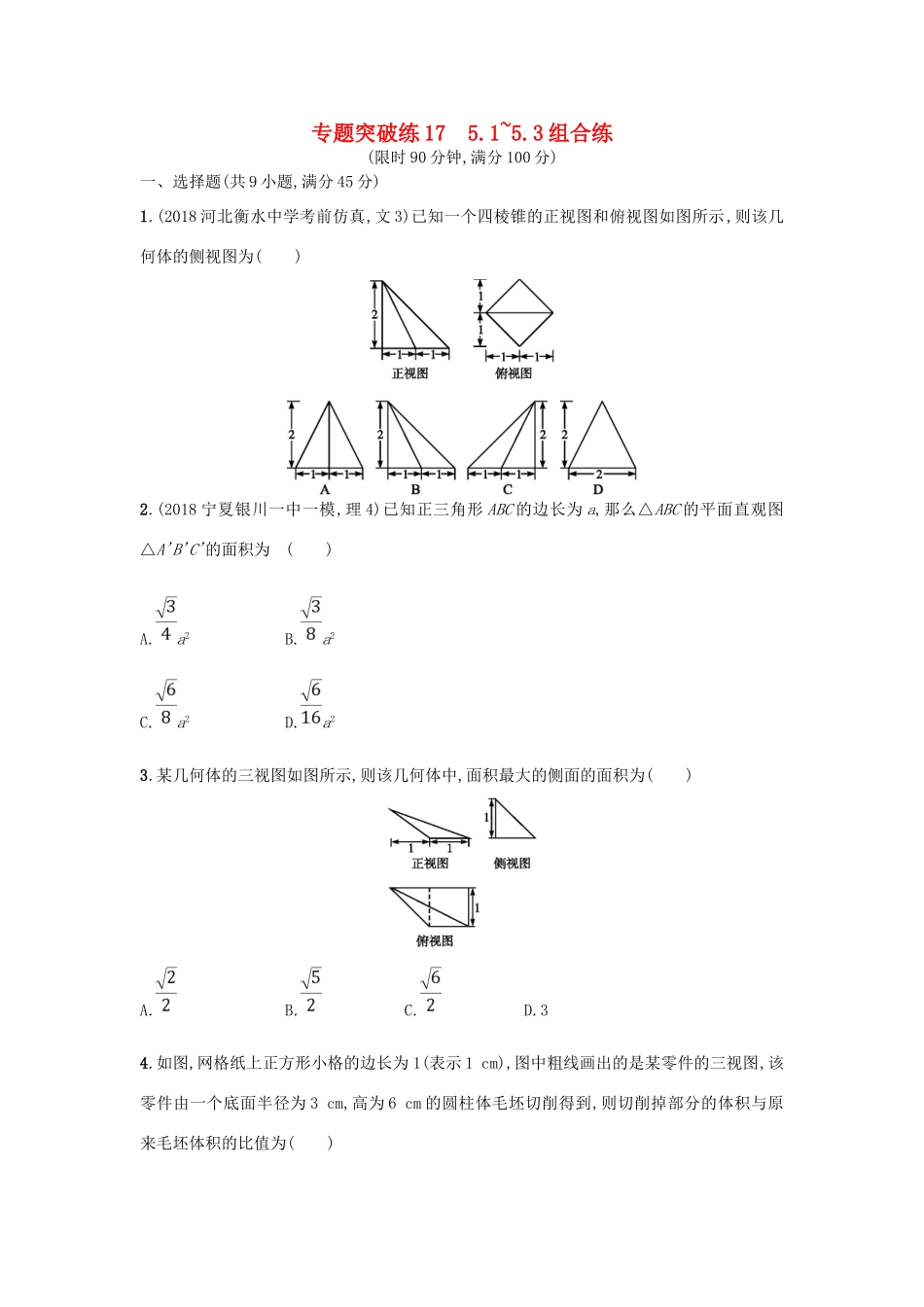
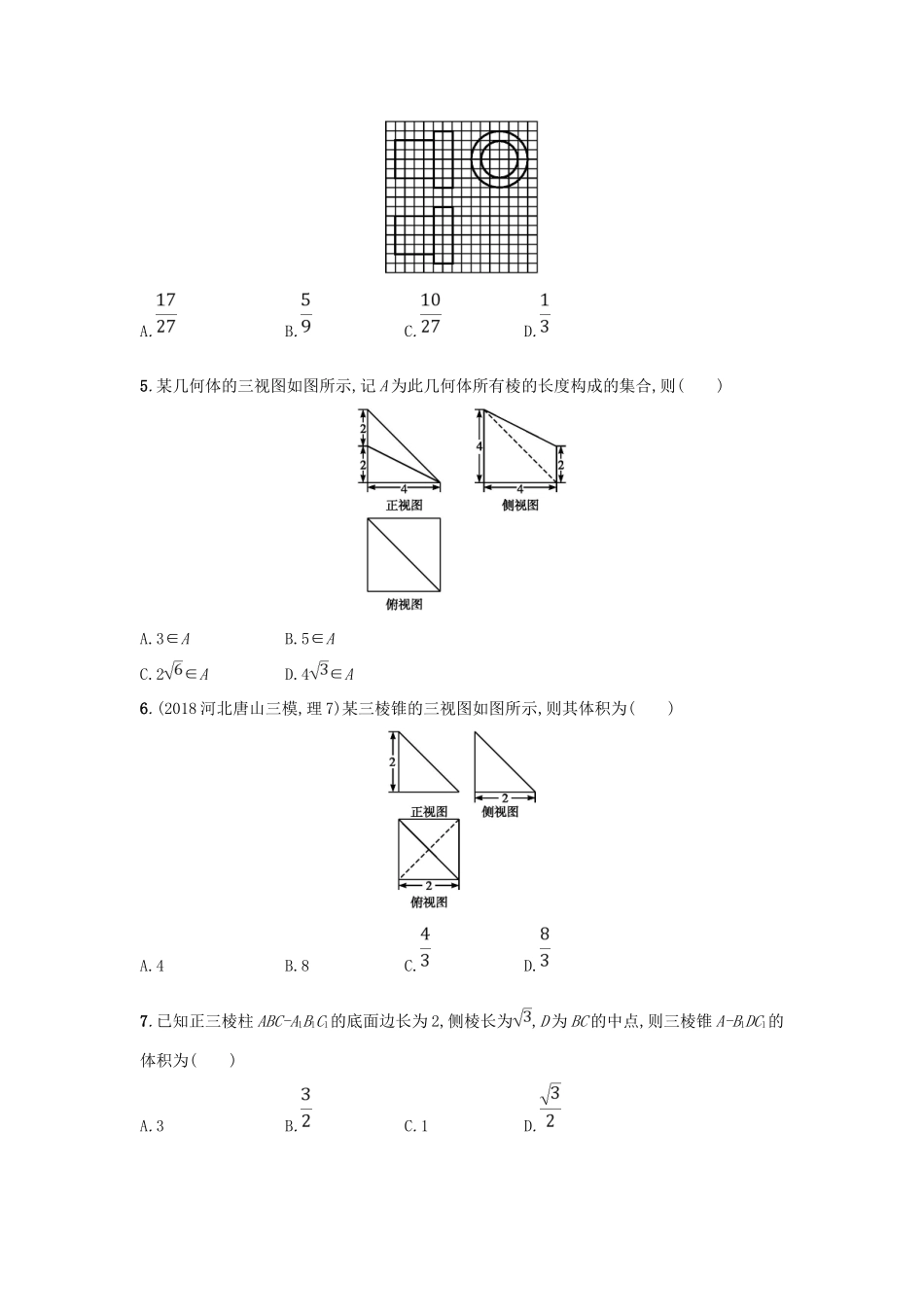
专题突破练175.1~5.3组合练(限时90分钟,满分100分)一、选择题(共9小题,满分45分)1.(2018河北衡水中学考前仿真,文3)已知一个四棱锥的正视图和俯视图如图所示,则该几何体的侧视图为()2.(2018宁夏银川一中一模,理4)已知正三角形ABC的边长为a,那么△ABC的平面直观图△A'B'C'的面积为()A.a2B.a2C.a2D.a23.某几何体的三视图如图所示,则该几何体中,面积最大的侧面的面积为()A.B.C.D.34.如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()A.B.C.D.5.某几何体的三视图如图所示,记A为此几何体所有棱的长度构成的集合,则()A.3∈AB.5∈AC.2∈AD.4∈A6.(2018河北唐山三模,理7)某三棱锥的三视图如图所示,则其体积为()A.4B.8C.D.7.已知正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为,D为BC的中点,则三棱锥A-B1DC1的体积为()A.3B.C.1D.8.(2018河南濮阳一模,理7)已知三棱锥A-BCD中,△ABD与△BCD是边长为2的等边三角形且二面角A-BD-C为直二面角,则三棱锥A-BCD的外接球的表面积为()A.B.5πC.6πD.9.(2018山西吕梁一模,文12)已知点A,B,C,D在同一个球的球面上,AB=BC=,AC=2,若四面体ABCD的体积为,球心O恰好在棱DA上,则这个球的表面积为()A.B.4πC.8πD.16π二、填空题(共3小题,满分15分)10.(2018江苏卷,10)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.11.(2018天津卷,文11)如图,已知正方体ABCD-A1B1C1D1的棱长为1,则四棱锥A1-BB1D1D的体积为.12.已知三棱锥A-BCD,AB=AC=BC=2,BD=CD=,点E是BC的中点,点A在平面BCD上的射影恰好为DE的中点F,则该三棱锥外接球的表面积为.三、解答题(共3个题,分别满分为13分,13分,14分)13.(2018江苏南京、盐城一模,15)如图所示,在直三棱柱ABC-A1B1C1中,CA=CB,点M,N分别是AB,A1B1的中点.(1)求证:BN∥平面A1MC;(2)若A1M⊥AB1,求证:AB1⊥A1C.14.(2018河南六市联考一,文19)如图,已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=,SB=,点E是棱AD的中点,点F在棱SC上,且=λ,SA∥平面BEF.(1)求实数λ的值;(2)求三棱锥F-EBC的体积.15.如图1,在边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A',连接EF,A'B,如图2.(1)求异面直线A'D与EF所成角的大小;(2)求三棱锥D-A'EF的体积.参考答案专题突破练175.1~5.3组合练1.A解析四棱锥的正视图和俯视图可知几何体的直观图如图所示,其侧视图为选项A.2.D解析如图①②所示的平面图形和直观图.由②可知,A'B'=AB=a,O'C'=OC=a,在图②中作C'D'⊥A'B'于D',则C'D'=O'C'=a.∴S△A'B'C'=A'B'·C'D'=×a×a=a2.3.B解析由三视图可知,几何体的直观图如图所示,平面AED⊥平面BCDE,四棱锥A-BCDE的高为1,四边形BCDE是边长为1的正方形,则S△AED=×1×1=,S△ABC=S△ABE=×1×,S△ACD=×1×,故选B.4.C解析由零件的三视图可知,该几何体为两个圆柱组合而成,如图所示.切削掉部分的体积V1=π×32×6-π×22×4-π×32×2=20π(cm3),原来毛坯体积V2=π×32×6=54π(cm3).故所求比值为.5.D解析根据三视图可知几何体是一个三棱柱截去一个三棱锥,如图所示,四边形ABCD是一个边长为4的正方形,且AF⊥面ABCD,DE∥AF,DE=4,AF=2,∴AF⊥AB,DE⊥DC,DE⊥BD,∴EC==4,EF=FB==2,BE==4. A为此几何体所有棱的长度构成的集合,∴A={2,4,4,4,2}.6.C解析由三棱锥的三视图得其直观图如下:几何体为底面是等腰直角三角形的三棱锥A-BCD,BC=CD=2,三棱锥的高为2,所以三棱锥的体积为V=×2×2×2=.7.C解析 D是等边三角形ABC的边BC的中点,∴AD⊥BC.又ABC-A1B1C1为正三棱柱,∴AD⊥平面BB1C1C. 四边形BB1C1C为矩形,∴×2×.又AD=2×,∴·AD==1.故选C.8.D解析如图所示.△ABD与△BCD是边长为2的等边三角形,且二面角A-BD-C为直二面角,设F,E分别为△ABD和△BCD的中心,则球心O为△ABD和△BCD的过中心的垂线的交点,所以OF=OE=FG=×2=.ED=×2=,则球半径r=,则S=4π×.9.D解析如图所示,设AC的中点为M,由已知得AB⊥BC,所以底面三角形ABC外接圆的圆心为M,所以OM⊥平面ABC,又OM∥DC,所以DC⊥平面ABC,由四...