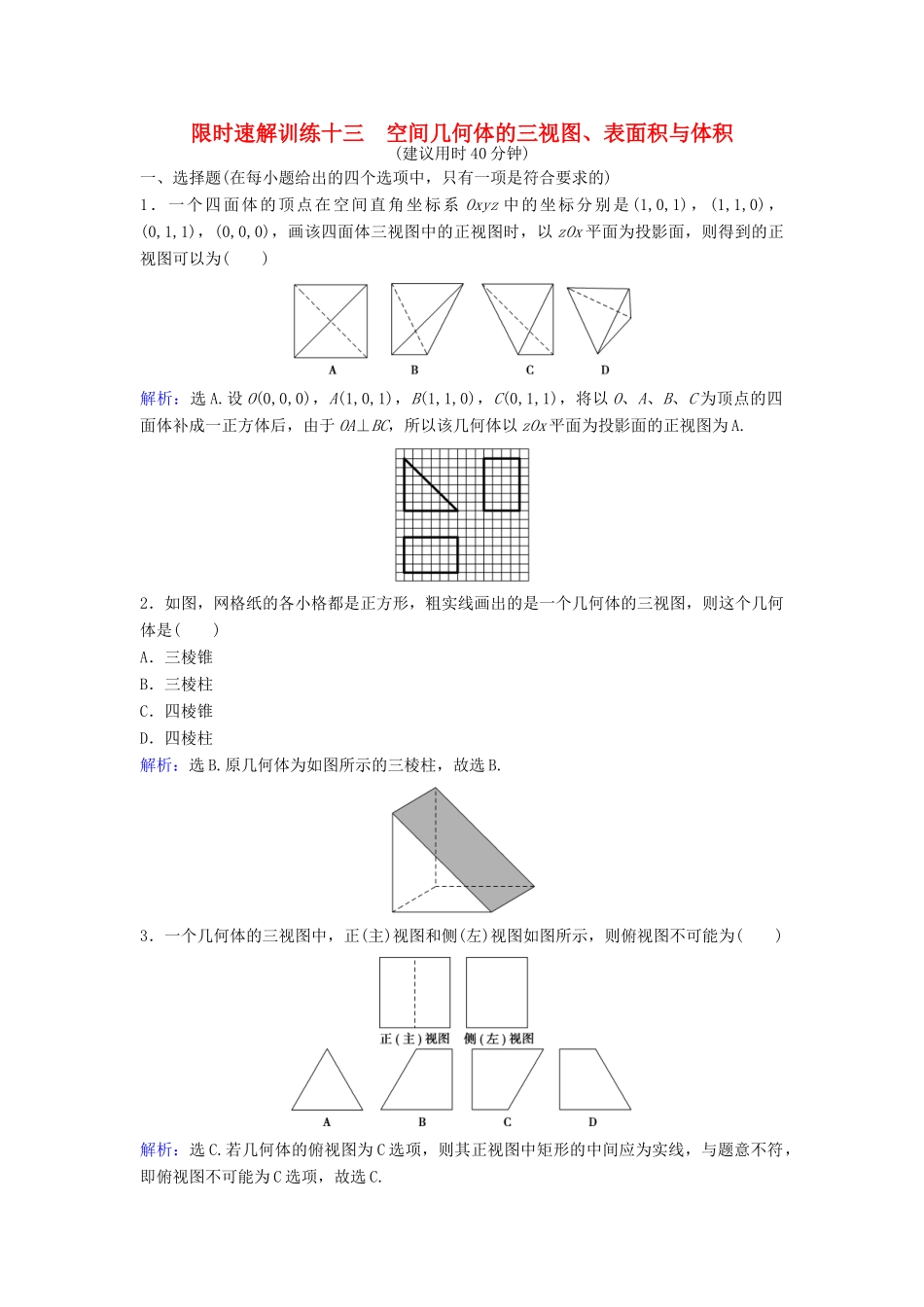
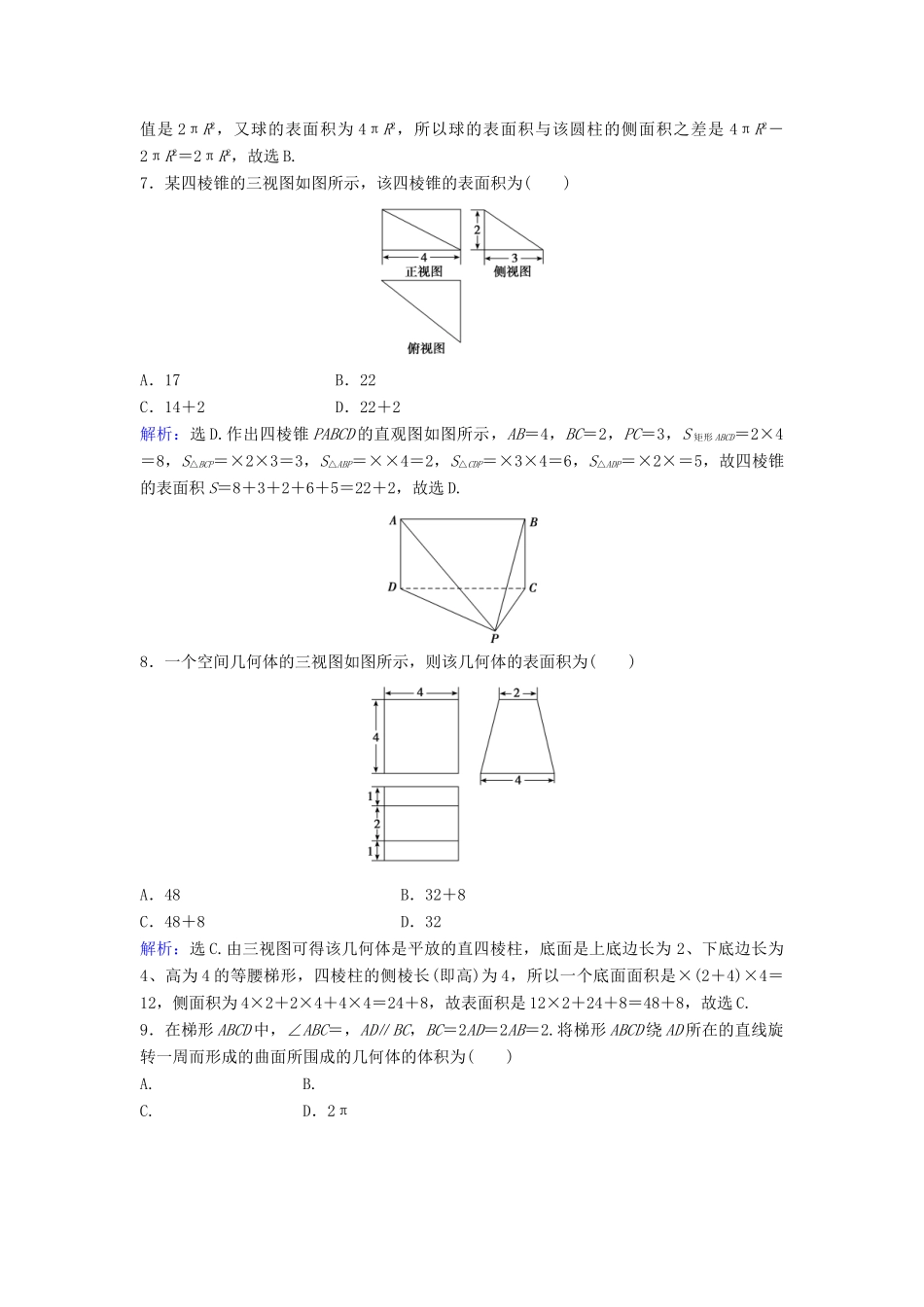
限时速解训练十三空间几何体的三视图、表面积与体积(建议用时40分钟)一、选择题(在每小题给出的四个选项中,只有一项是符合要求的)1.一个四面体的顶点在空间直角坐标系Oxyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可以为()解析:选A.设O(0,0,0),A(1,0,1),B(1,1,0),C(0,1,1),将以O、A、B、C为顶点的四面体补成一正方体后,由于OA⊥BC,所以该几何体以zOx平面为投影面的正视图为A.2.如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是()A.三棱锥B.三棱柱C.四棱锥D.四棱柱解析:选B.原几何体为如图所示的三棱柱,故选B.3.一个几何体的三视图中,正(主)视图和侧(左)视图如图所示,则俯视图不可能为()解析:选C.若几何体的俯视图为C选项,则其正视图中矩形的中间应为实线,与题意不符,即俯视图不可能为C选项,故选C.4.某四棱锥的三视图如图所示,记A为此棱锥所有棱的长度的集合,则()A.2∈A,且4∈AB.∈A,且4∈AC.2∈A,且2∈AD.∈A,且∈A解析:选D.由俯视图可知,该四棱锥的底面边长为,由主视图可知四棱锥的高为4,所以其侧棱长为=,故选D.5.如图是一个空间几何体的三视图,则该几何体的表面三角形中为直角三角形的个数为()A.2B.3C.4D.5解析:选C.作出三棱锥的直观图如图所示,由三视图可知AB=BD=2,BC=CD=,AD=2,AC=,故△ABC,△ACD,△ABD,△BCD均为直角三角形,故选C.6.半径为R的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是()A.πR2B.2πR2C.3πR2D.4πR2解析:选B.设球的内接圆柱的底面圆半径为r,母线长为l,则2+r2=R2,该圆柱的侧面积为2πrl=π=π≤π×=2πR2,当且仅当l=R时取等号,所以该圆柱的侧面积的最大值是2πR2,又球的表面积为4πR2,所以球的表面积与该圆柱的侧面积之差是4πR2-2πR2=2πR2,故选B.7.某四棱锥的三视图如图所示,该四棱锥的表面积为()A.17B.22C.14+2D.22+2解析:选D.作出四棱锥PABCD的直观图如图所示,AB=4,BC=2,PC=3,S矩形ABCD=2×4=8,S△BCP=×2×3=3,S△ABP=××4=2,S△CDP=×3×4=6,S△ADP=×2×=5,故四棱锥的表面积S=8+3+2+6+5=22+2,故选D.8.一个空间几何体的三视图如图所示,则该几何体的表面积为()A.48B.32+8C.48+8D.32解析:选C.由三视图可得该几何体是平放的直四棱柱,底面是上底边长为2、下底边长为4、高为4的等腰梯形,四棱柱的侧棱长(即高)为4,所以一个底面面积是×(2+4)×4=12,侧面积为4×2+2×4+4×4=24+8,故表面积是12×2+24+8=48+8,故选C.9.在梯形ABCD中,∠ABC=,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为()A.B.C.D.2π解析:选C.过点C作CE垂直AD所在直线于点E,梯形ABCD绕AD所在直线旋转一周所形成的旋转体是由以线段AB的长为底面圆半径,线段BC为母线的圆柱挖去以线段CE的长为底面圆半径,ED为高的圆锥,如图所示,该几何体的体积为V=V圆柱-V圆锥=π·AB2·BC-·π·CE2·DE=π×12×2-π×12×1=,故选C.10.(2016·山东淄博一模)某几何体的三视图如图所示,图中的四边形都是边长为1的正方体,其中正(主)视图、侧(左)视图中的两条虚线互相垂直,则该几何体的体积是()A.B.C.D.解析:选A.由三视图可知该几何体为一正方体挖去一个倒置且高为的正四棱锥,所以该几何体的体积为1-××1×1=.故选A.11.(2016·吉林长春一模)下图为一个半球挖去一个圆锥后的几何体的三视图,则该几何体的表面积为()A.πB.πC.(4+2)πD.(8+4)π解析:选D.该几何体的表面积为半球面积与圆锥侧面积之和,即S=·4πr2+πrl=8π+4π=(8+4)π.故选D.12.某几何体的三视图如图所示,当xy最大时,该几何体的体积为()A.2B.4C.8D.16解析:选D.该几何体的直观图如图所示,由直观图可知PA2=102-y2=x2-(2)2,∴x2+y2=128.又 128=x2+y2≥2xy,当且仅当x=y时xy取得最大值,∴此时∴∴h=PA=6,∴V=·S△ABC·|PA|...