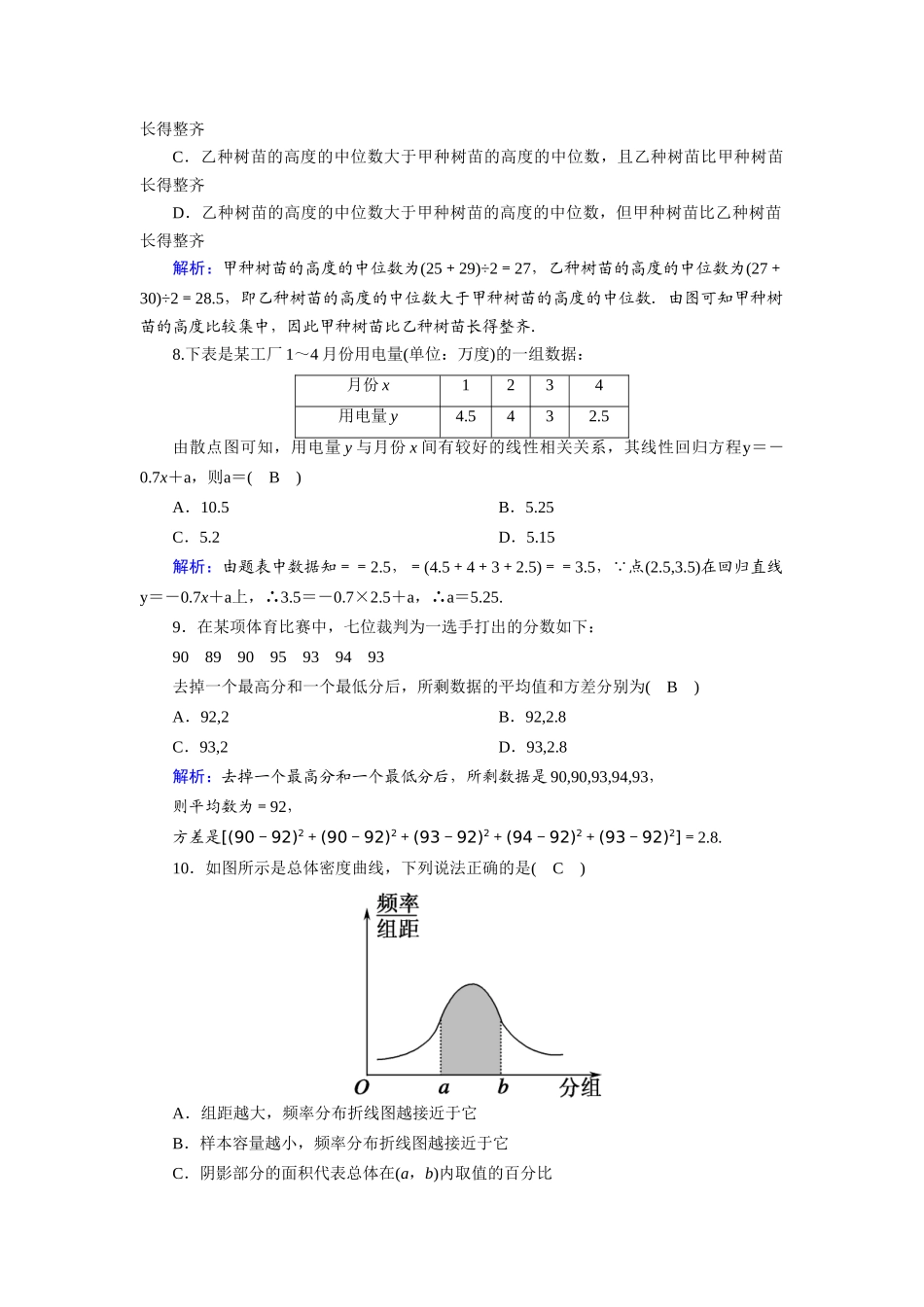
第二章检测试题时间:90分钟分值:120分第Ⅰ卷(选择题,共60分)一、选择题(每小题5分,共60分)1.下列变量是线性相关的是(C)A.人的身高与视力B.角的大小与所对的圆弧长C.收入水平与纳税水平D.人的年龄与身高解析:A,D中两个变量不具有线性相关关系,B中两个变量是函数关系.2.为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是(B)A.x1,x2,…,xn的平均数B.x1,x2,…,xn的标准差C.x1,x2,…,xn的最大值D.x1,x2,…,xn的中位数解析:刻画评估这种农作物亩产量稳定程度的指标是标准差,故选B.3.某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本,若样本中的青年职工为7人,则样本容量为(B)A.7B.15C.25D.35解析:由题意设样本容量为n,则=,解得n=15.4.有一个容量为66的样本,数据的分组及各组的频数如下:[11.5,15.5)2[15.5,19.5)4[19.5,23.5)9[23.5,27.5)18[27.5,31.5)11[31.5,35.5)12[35.5,39.5)7[39.5,43.5)3根据样本的频率分布估计,大于或等于31.5的数据约占(B)A.B.C.D.解析:由题意知,样本的容量为66,而落在[31.5,43.5)内的样本数为12+7+3=22,故大于或等于31.5的数据约占=.5.总体由编号为01,02,…,19,20的20个个体组成.利用下面的随机数表选取6个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第6个个体的编号为(D)7816657208026314070243699728019832049234493582003623486969387481A.08B.07C.02D.04解析:从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出的数字为08,02,14,07,01,04,故选出的第6个个体的编号为04.6.如图为某个容量为100的样本的频率分布直方图,分组为[96,98),[98,100),[100,102),[102,104),[104,106),则在区间[98,100)上的频数为(C)A.0.100B.0.200C.20D.10解析:区间[98,100)上小矩形的面积为0.100×2=0.200,即频率为0.200,所以区间[98,100)上的频数为100×0.200=20.7.林管部门在每年植树节前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两种树苗中各抽测了10株树苗的高度,其茎叶图如图所示.根据茎叶图,下列描述正确的是(D)A.甲种树苗的高度的中位数大于乙种树苗的高度的中位数,且甲种树苗比乙种树苗长得整齐B.甲种树苗的高度的中位数大于乙种树苗的高度的中位数,但乙种树苗比甲种树苗长得整齐C.乙种树苗的高度的中位数大于甲种树苗的高度的中位数,且乙种树苗比甲种树苗长得整齐D.乙种树苗的高度的中位数大于甲种树苗的高度的中位数,但甲种树苗比乙种树苗长得整齐解析:甲种树苗的高度的中位数为(25+29)÷2=27,乙种树苗的高度的中位数为(27+30)÷2=28.5,即乙种树苗的高度的中位数大于甲种树苗的高度的中位数.由图可知甲种树苗的高度比较集中,因此甲种树苗比乙种树苗长得整齐.8.下表是某工厂1~4月份用电量(单位:万度)的一组数据:月份x1234用电量y4.5432.5由散点图可知,用电量y与月份x间有较好的线性相关关系,其线性回归方程y=-0.7x+a,则a=(B)A.10.5B.5.25C.5.2D.5.15解析:由题表中数据知==2.5,=(4.5+4+3+2.5)==3.5, 点(2.5,3.5)在回归直线y=-0.7x+a上,∴3.5=-0.7×2.5+a,∴a=5.25.9.在某项体育比赛中,七位裁判为一选手打出的分数如下:90899095939493去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为(B)A.92,2B.92,2.8C.93,2D.93,2.8解析:去掉一个最高分和一个最低分后,所剩数据是90,90,93,94,93,则平均数为=92,方差是[(90-92)2+(90-92)2+(93-92)2+(94-92)2+(93-92)2]=2.8.10.如图所示是总体密度曲线,下列说法正确的是(C)A.组距越大,频率分布折线图越接近于它B.样本容量越小,频率分布折线图越接近于它C.阴影部分的面积代表总体在(a,b)内取值的百分比D.阴影部分的平均高度代表总体在(a,b)内取值的百分...