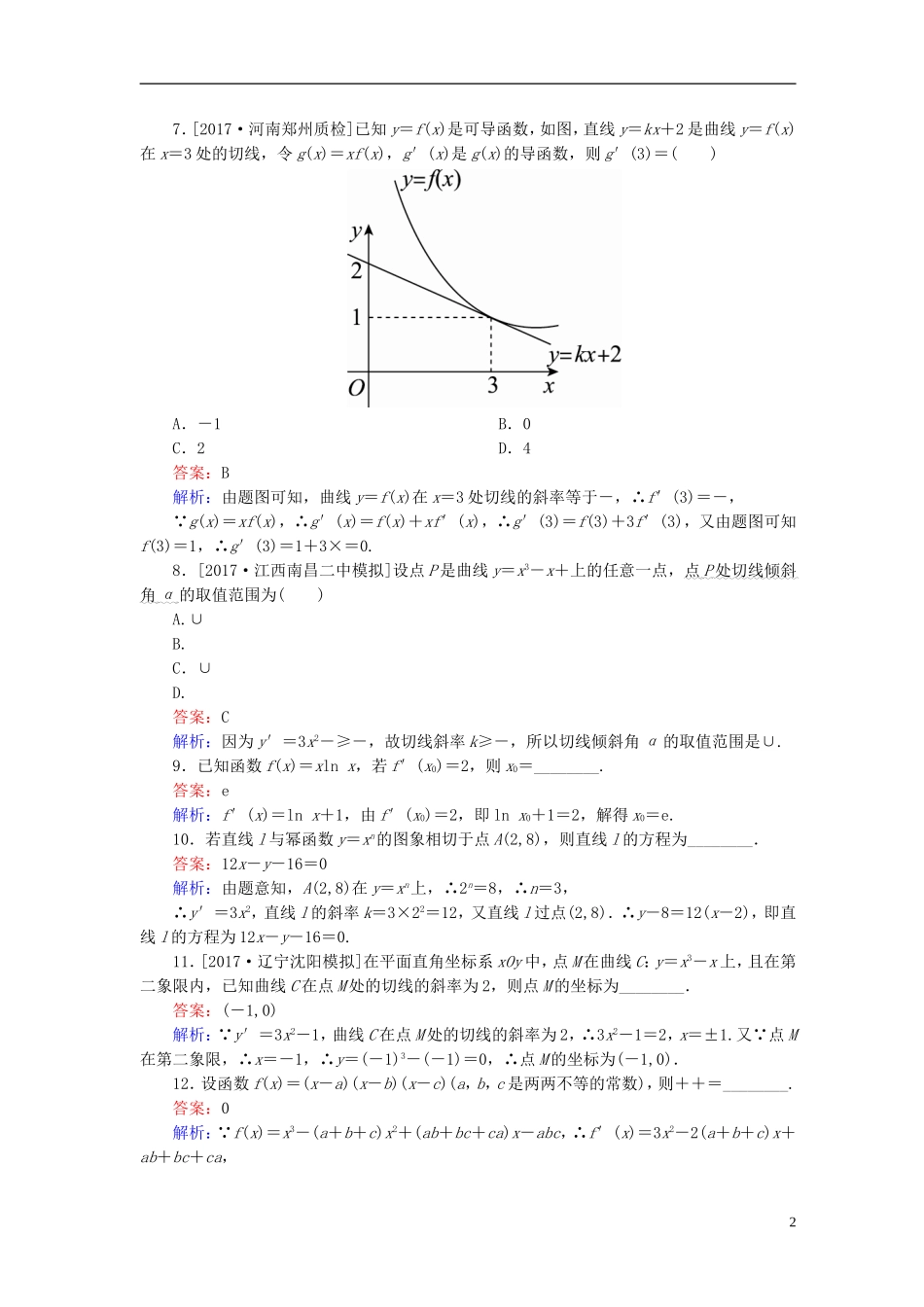
课时跟踪检测(十三)[高考基础题型得分练]1.函数f(x)=(x+2a)(x-a)2的导数为()A.2(x2-a2)B.2(x2+a2)C.3(x2-a2)D.3(x2+a2)答案:C解析: f(x)=(x+2a)(x-a)2=x3-3a2x+2a3,∴f′(x)=3(x2-a2).2.曲线y=sinx+ex在点(0,1)处的切线方程是()A.x-3y+3=0B.x-2y+2=0C.2x-y+1=0D.3x-y+1=0答案:C解析: y=sinx+ex,∴y′=cosx+ex,∴y′|x=0=cos0+e0=2,∴曲线y=sinx+ex在点(0,1)处的切线方程为y-1=2(x-0),即2x-y+1=0.3.[2017·山东师大附中月考]曲线y=ax在x=0处的切线方程是xln2+y-1=0,则a=()A.B.2C.ln2D.ln答案:A解析:由题知y′=axlna,y′|x=0=lna,又切点为(0,1),故切线方程为xlna-y+1=0,∴a=.4.若f(x)=2xf′(1)+x2,则f′(0)=()A.2B.0C.-2D.-4答案:D解析:f′(x)=2f′(1)+2x,∴令x=1,得f′(1)=-2,∴f′(0)=2f′(1)=-4.5.[2017·河北保定调研]已知曲线y=lnx的切线过原点,则此切线的斜率为()A.eB.-eC.D.-答案:C解析:y=lnx的定义域为(0,+∞),且y′=,设切点为(x0,lnx0),则y′|x=x0=,切线方程为y-lnx0=(x-x0).因为切线过点(0,0),所以-lnx0=-1,解得x0=e,故此切线的斜率为.6.[2017·广东湛江调研]曲线y=e-2x+1在点(0,2)处的切线与直线y=0和y=x围成的三角形的面积为()A.B.C.D.1答案:A解析:y′|x=0=(-2e-2x)|x=0=-2,故曲线y=e-2x+1在点(0,2)处的切线方程为y=-2x+2,易得切线与直线y=0和y=x的交点分别为(1,0),,故围成的三角形的面积为×1×=.17.[2017·河南郑州质检]已知y=f(x)是可导函数,如图,直线y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),g′(x)是g(x)的导函数,则g′(3)=()A.-1B.0C.2D.4答案:B解析:由题图可知,曲线y=f(x)在x=3处切线的斜率等于-,∴f′(3)=-, g(x)=xf(x),∴g′(x)=f(x)+xf′(x),∴g′(3)=f(3)+3f′(3),又由题图可知f(3)=1,∴g′(3)=1+3×=0.8.[2017·江西南昌二中模拟]设点P是曲线y=x3-x+上的任意一点,点P处切线倾斜角α的取值范围为()A.∪B.C.∪D.答案:C解析:因为y′=3x2-≥-,故切线斜率k≥-,所以切线倾斜角α的取值范围是∪.9.已知函数f(x)=xlnx,若f′(x0)=2,则x0=________.答案:e解析:f′(x)=lnx+1,由f′(x0)=2,即lnx0+1=2,解得x0=e.10.若直线l与幂函数y=xn的图象相切于点A(2,8),则直线l的方程为________.答案:12x-y-16=0解析:由题意知,A(2,8)在y=xn上,∴2n=8,∴n=3,∴y′=3x2,直线l的斜率k=3×22=12,又直线l过点(2,8).∴y-8=12(x-2),即直线l的方程为12x-y-16=0.11.[2017·辽宁沈阳模拟]在平面直角坐标系xOy中,点M在曲线C:y=x3-x上,且在第二象限内,已知曲线C在点M处的切线的斜率为2,则点M的坐标为________.答案:(-1,0)解析: y′=3x2-1,曲线C在点M处的切线的斜率为2,∴3x2-1=2,x=±1.又 点M在第二象限,∴x=-1,∴y=(-1)3-(-1)=0,∴点M的坐标为(-1,0).12.设函数f(x)=(x-a)(x-b)(x-c)(a,b,c是两两不等的常数),则++=________.答案:0解析: f(x)=x3-(a+b+c)x2+(ab+bc+ca)x-abc,∴f′(x)=3x2-2(a+b+c)x+ab+bc+ca,2f′(a)=(a-b)(a-c),f′(b)=(b-a)(b-c),f′(c)=(c-a)(c-b).∴++=++==0.[冲刺名校能力提升练]1.[2017·广东惠州模拟]已知函数f(x)=cosx,则f(π)+f′=()A.-B.-C.-D.-答案:C解析: f′(x)=-cosx+(-sinx),∴f(π)+f′=-+·(-1)=-.2.设曲线y=在点处的切线与直线x-ay+1=0平行,则实数a等于()A.-1B.C.-2D.2答案:A解析: y′=,∴y′x==-1,由条件知=-1,∴a=-1.3.[2017·江西上饶模拟]若点P是曲线y=x2-lnx上任意一点,则点P到直线y=x-2的最小值为()A.1B.C.D.答案:B解析:因为定义域为(0,+∞),所以y′=2x-=1,解得x=1,则在P(1,1)处的切线方程为x-y=0,所以两平行线间的距离为d==.4.已知函数f(x)=,g(x)=alnx,a∈R,若曲线...