第26章二次函数单元复习课件（人教版九年级下）(1)VIP免费

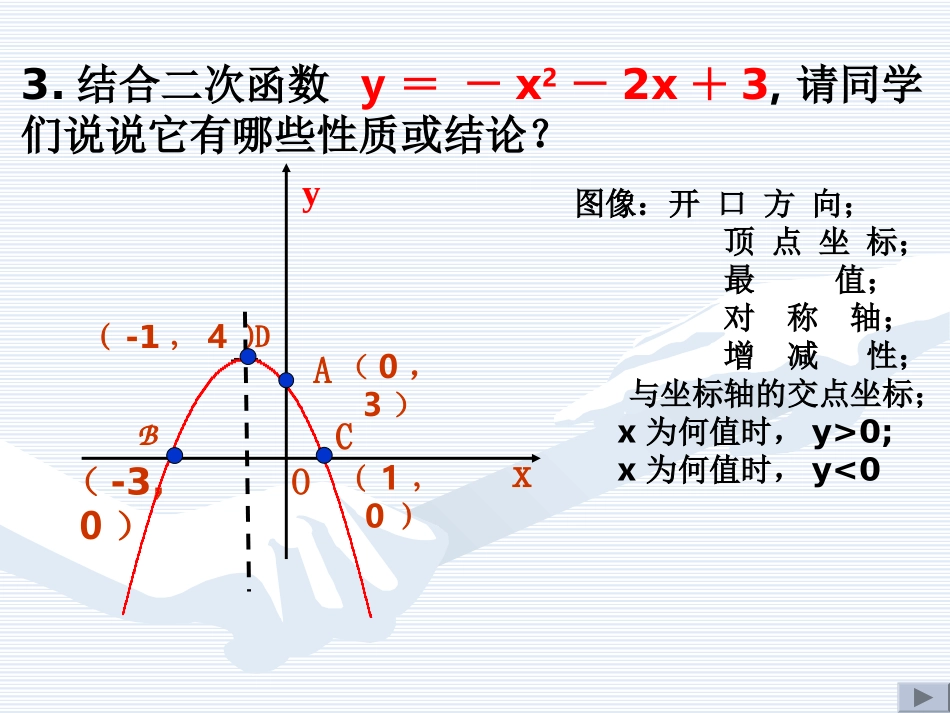
二次函数复习(1)题组一梳理知识，关注数学思想方法1、下列函数中，是二次函数的是.①②③④⑤⑥⑦⑧142xxy22xyxy4pnxmxy2xy32.当m_______时,函数y=(m+1)χ-2χ+1是二次函数？mm2)1)(2(3xxy4)1(212xy①②③⑦=222)1(xxy3.结合二次函数y＝－x2－2x＋3,请同学们说说它有哪些性质或结论？（-3,0）（-1，4）（1，0）（0，3）yCDxOBA图像：开口方向；顶点坐标；最值；对称轴；增减性；与坐标轴的交点坐标；x为何值时，y>0;x为何值时，y<04.如图是某二次函数的图象,根据图象,你如何确定该函数的解析式？有几种办法？y（1，0）（-1，4）xO（-3，0）（0，3）请思考：解决上述问题的过程中，(1)我们复习了二次函数的哪些内容？(2)你在解题过程中运用了哪些数学思想方法？例、已知二次函数的最大值是2，图象顶点在直线y=x+1上，并且图象经过点（3，-6）。求该二次函数的解析式。解：∵二次函数的最大值是2∴抛物线的顶点纵坐标为2又∵抛物线的顶点在直线y=x+1上∴当y=2时，x=1∴顶点坐标为（1，2）∴设二次函数的解析式为y=a(x-1)2+2又∵图象经过点（3，-6）∴-6=a(3-1)2+2a=-2∴∴二次函数的解析式为y=-2(x-1)2+2即：y=-2x2+4x（1）.已知抛物线C1的解析式是y＝－x2－2x＋3，把抛物线C1向右平移３个单位,在向下平移4个单位，则抛物线C2的解析式__________y（1，0）（-1，4）xO（-3，0）1.平移问题题组二分析典型问题，归纳解题策略y=-x²-4x-4（2）抛物线y=4(x-2)²-5向上平移1个单位,再向左平移3个单位后解析式为AABBCCDD2yaxc下列各图中可能是函数与()的图象的是()ayx0,0ac√√►考点一抛物线和其他函数图象的共存问题►考点一抛物线和其他函数图象的共存问题在同一直角坐标系中，一次函数y＝ax＋b和二次函数y＝ax²＋bx的图象可能为()A巩固练习11、、aa、、bb、、cc22、、33、、a+b+ca+b+c；；a-b+ca-b+c44、、4a-2b+c4a+2b+c；55、、2a+b;2a-b2a+b;2a-b1xy0－1acb42►考点二根据图象判断系数及含有系数的代数式的符号-2数学·新课标（RJ）C已知二次函数y＝ax²＋bx＋c(a≠0)的图象如图26－2所示，则下列结论．错误的有()①ac>0；②b<0；③a－b＋c<0；④a＋b＋c<0；⑤2a＋b＝0.A．1个B．2个C．3个D．4个C请思考：解决上述问题的过程中，你用到了哪些解题方法？1.如图,抛物线y=ax2+bx+c,请判断下列各式的符号：①a0;②c0;③b2-4ac0;④b0;xyO题组三在练习中印证归纳结题组三在练习中印证归纳结果果2：若抛物线的图象如图，则a=.2：若抛物线的图象如图，则a=.2231yaxxa3：若抛物线的图象如图，则△ABC的面积是。3：若抛物线的图象如图，则△ABC的面积是。243yxxAABBCC5已知函数y=-x²-x-4，当函数值y随x的增大而减小时，x的取值范围是___________4已知y=（k+2）x是二次函数，且当x>0时，y随X增大而增大，则k=___.K²+k-4题组三在练习中印证归纳结果题组三在练习中印证归纳结果题组三在练习中印证归纳结果题组三在练习中印证归纳结果6．如图，若将抛物线y＝(x＋1)2－7沿x轴平移，使平移后的图象经过P(－2,2)，求平移后抛物线的解析式．(0,1.6)(0,1.6)20.1()2.5yxk1.6m3丁丁推铅球的出手高度为,在如图所示①求k的值的直角坐标系中，铅球的运行路线近似为抛物线xyO②求铅球的落点与丁丁的距离③一个1.5m的小朋友跑到离原点6米的地方(如图)，他会受到伤害吗？学以致用回顾反思回顾反思11、本节课着重考查了哪些知识？、本节课着重考查了哪些知识？22、你又加深了对哪些数学思想方法的理解、你又加深了对哪些数学思想方法的理解？？33、你能归纳出哪些问题的解题策略？、你能归纳出哪些问题的解题策略？环节四环节四————通过反思提升对学习过程的认知作业：1.必做：教材56页：复习题221—5小题做完2.选做：教材66页：第6题3.补充题：已知抛物线y=ax2+bx+c与x轴正、负半轴分别交于A、B两点，与y轴负半轴交于点C。若OA=4，OB=1，∠ACB=90°，求抛物线解析式。ABxyOC欢迎指导!欢迎指导!再见