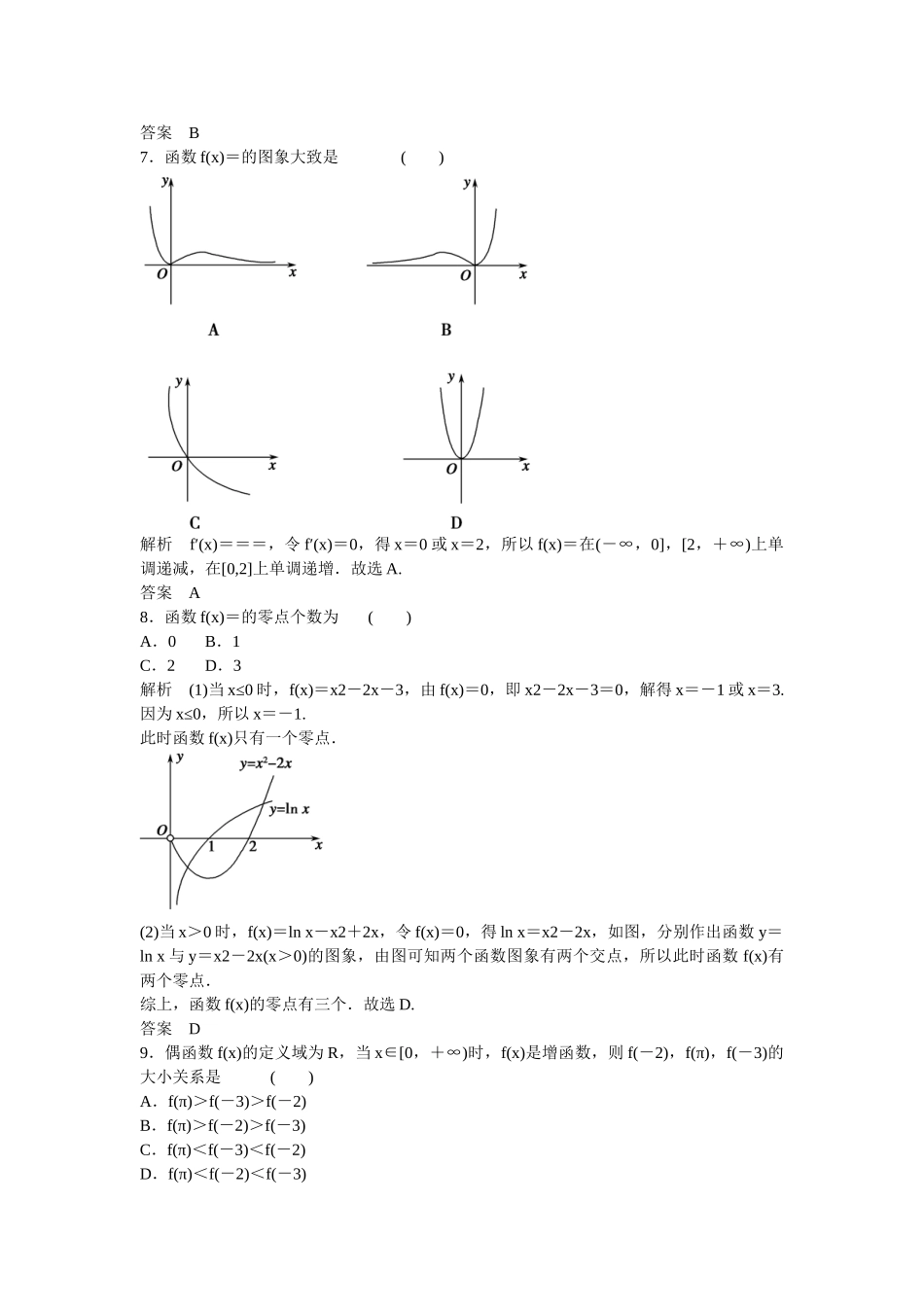
【创新设计】届高考数学一轮复习探究课1课时作业文新人教A版(建议用时:45分钟)一、选择题1.下列函数中,在其定义域内既是奇函数又是减函数的是()A.y=lgB.y=x+C.y=tanxD.y=解析对于选项B,C,D,函数在定义域内是奇函数,但不是减函数.答案A2.函数f(x)=+的定义域为()A.(0,2]B.(0,2)C.(0,1)∪(1,2]D.(-∞,2]解析由题意知又x>0,解得0<x≤2且x≠1.答案C3.已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x2+1,则f(1)+g(1)=()A.-3B.-1C.1D.3解析因为f(x),g(x)分别是定义在R上的偶函数和奇函数,所以f(-1)=f(1),g(-1)=-g(1).因为f(x)-g(x)=x3+x2+1,所以f(-1)-g(-1)=(-1)3+(-1)2+1=1,即f(1)+g(1)=1.答案C4.设函数f(x)=若f(a)+f(-1)=3,则a=()A.eB.C.1D.e或解析因为f(-1)=-1=2,所以f(a)=3-2=1.当a>0时,|lna|=1,解得a=e或;当a<0时,a=1,无解.答案D5.若0<m<1,则()A.logm(1+m)>logm(1-m)B.logm(1+m)>0C.1-m>(1+m)2D.(1-m)>(1-m)解析若0<m<1,则f(x)=logmx在定义域内单调递减,所以logm(1+m)<logm(1-m),logm(1+m)<logm1=0,选项A,B错误;(1+m)2>1>1-m,选项C错误;0<1-m<1,所以f(x)=(1-m)x在定义域内单调递减,所以(1-m)>(1-m),选项D正确.答案D6.函数f(x)=2x-x2的值域为()A.RB.C.[1,+∞)D.(0,+∞)解析指数函数y=x在定义域内单调递减,而2x-x2=-(x-1)2+1≤1,所以f(x)=2x-x2≥1=.所以函数f(x)=2x-x2的值域为.答案B7.函数f(x)=的图象大致是()解析f′(x)===,令f′(x)=0,得x=0或x=2,所以f(x)=在(-∞,0],[2,+∞)上单调递减,在[0,2]上单调递增.故选A.答案A8.函数f(x)=的零点个数为()A.0B.1C.2D.3解析(1)当x≤0时,f(x)=x2-2x-3,由f(x)=0,即x2-2x-3=0,解得x=-1或x=3.因为x≤0,所以x=-1.此时函数f(x)只有一个零点.(2)当x>0时,f(x)=lnx-x2+2x,令f(x)=0,得lnx=x2-2x,如图,分别作出函数y=lnx与y=x2-2x(x>0)的图象,由图可知两个函数图象有两个交点,所以此时函数f(x)有两个零点.综上,函数f(x)的零点有三个.故选D.答案D9.偶函数f(x)的定义域为R,当x∈[0,+∞)时,f(x)是增函数,则f(-2),f(π),f(-3)的大小关系是()A.f(π)>f(-3)>f(-2)B.f(π)>f(-2)>f(-3)C.f(π)<f(-3)<f(-2)D.f(π)<f(-2)<f(-3)解析 偶函数f(x)的定义域为R,在[0,+∞)上单调递增,∴在区间(-∞,0]上,f(x)是减函数,f(-π)=f(π),∴f(π)>f(-3)>f(-2).答案A10.已知函数f(x)=ln(-3x)+1,则f(lg2)+f=()A.-1B.0C.1D.2解析设F(x)=f(x)-1=ln(-3x),该函数的定义域为R.而F(-x)=f(-x)-1=ln(+3x),所以F(x)+F(-x)=ln(-3x)+ln(+3x)=ln[(-3x)(+3x)]=ln1=0,所以函数F(x)为奇函数.又lg=-lg2,所以F(lg2)+F=F(lg2)+F(-lg2)=0,即[f(lg2)-1]+=0,整理,得f(lg2)+f=2.故选D.答案D11.方程+ln=0的解为x0,则x0所在的大致区间是()A.(1,2)B.(2,3)C.(3,4)D.(1,2)与(2,3)解析设f(x)=+ln=-ln(x-1),函数f(x)的定义域为(1,+∞).当1<x<2时,ln(x-1)<0,>0,所以f(x)>0,故函数在(1,2)内没有零点.因为f(2)=-ln1=1>0,f(3)=-ln2=,又=2≈2.828,所以>e,故lne<ln,即1<ln8=ln2,所以2<3ln2,即f(3)<0.又f(4)=-ln3=-ln3<0,根据零点存在性定理,可知函数f(x)在(2,3)上必存在一个零点x0,即方程+ln=0的解x0∈(2,3).故选B.答案B12.定义在R上的函数f(x)满足f(x+2)+f(x)=0,且函数f(x)为奇函数.给出下列结论:①函数f(x)的最小正周期为4;②函数f(x)的图象关于点(0,0)对称;③函数f(x)的图象关于x=2对称;④函数f(x)的最大值为f(2).其中一定正确的命题序号是()A.①②B.②③C.③④D.①④解析由f(x+2)+f(x)=0,可得f(x+4)=-f(x+2)=f(x),∴其最小正周期是4;由函数f(x)为奇函数,可知函数f(x)的图象关于点(0,0)对称;函数的轴对称性、最值无法作出判断.答案A二...