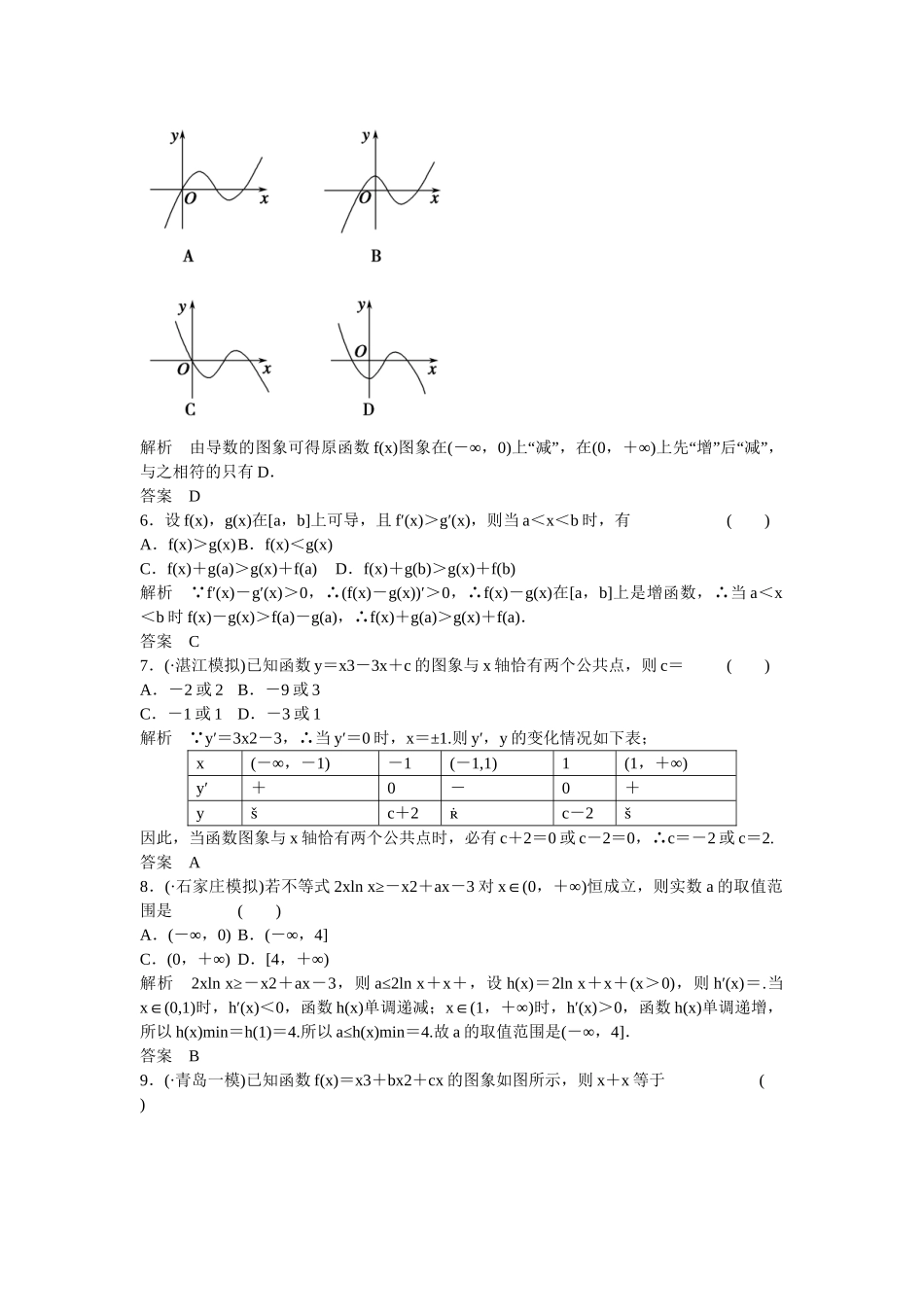
阶段回扣练3导数及其应用(建议用时:90分钟)一、选择题1.(·哈师大附中检测)设函数f(x)=axlnx(a∈R,a≠0),若f′(e)=2,则f(e)的值为()A.1B.C.eD.2e解析f′(x)=alnx+a,故f′(e)=2a=2,得a=1,故f(x)=xlnx,f(e)=e.答案C2.(·大连模拟)曲线y=x2+lnx在点(1,1)处的切线方程为()A.3x-y-2=0B.x-3y+2=0C.3x+y-4=0D.x+3y-4=0解析y′=2x+,故y′|x=1=3,故在点(1,1)处的切线方程为y-1=3(x-1),化简整理得3x-y-2=0.答案A3.三次函数f(x)=mx3-x在(∞∞-,+)上是减函数,则m的取值范围是()A.(∞-,0)B.(∞-,1)C.(∞-,0]D.(∞-,1]解析f′(x)=3mx2-1,依题意可得m<0.答案A4.设函数g(x)=x(x2-1),则g(x)在区间[0,1]上的最小值为()A.-1B.0C.-D.解析g(x)=x3-x,由g′(x)=3x2-1=0,解得x=或-(舍去).当x变化时,g′(x)与g(x)的变化情况如下表:x01g′(x)-0+g(x)0极小值0所以当x=时,g(x)有最小值g=-.答案C5.(·济宁一模)已知函数f(x)的导函数f′(x)=ax2+bx+c的图象如图所示,则函数f(x)的图象可能是()解析由导数的图象可得原函数f(x)图象在(∞-,0)“”上减,在(0∞,+)“”“”上先增后减,与之相符的只有D.答案D6.设f(x),g(x)在[a,b]上可导,且f′(x)>g′(x),则当a<x<b时,有()A.f(x)>g(x)B.f(x)<g(x)C.f(x)+g(a)>g(x)+f(a)D.f(x)+g(b)>g(x)+f(b)解析 f′(x)-g′(x)>0,∴(f(x)-g(x))′>0,∴f(x)-g(x)在[a,b]上是增函数,∴当a<x<b时f(x)-g(x)>f(a)-g(a),∴f(x)+g(a)>g(x)+f(a).答案C7.(·湛江模拟)已知函数y=x3-3x+c的图象与x轴恰有两个公共点,则c=()A.-2或2B.-9或3C.-1或1D.-3或1解析 y′=3x2-3,∴当y′=0时,x=±1.则y′,y的变化情况如下表;x(∞-,-1)-1(-1,1)1(1∞,+)y′+0-0+yc+2c-2因此,当函数图象与x轴恰有两个公共点时,必有c+2=0或c-2=0,∴c=-2或c=2.答案A8.(·石家庄模拟)若不等式2xlnx≥-x2+ax-3对x∈(0∞,+)恒成立,则实数a的取值范围是()A.(∞-,0)B.(∞-,4]C.(0∞,+)D.[4∞,+)解析2xlnx≥-x2+ax-3,则a≤2lnx+x+,设h(x)=2lnx+x+(x>0),则h′(x)=.当x∈(0,1)时,h′(x)<0,函数h(x)单调递减;x∈(1∞,+)时,h′(x)>0,函数h(x)单调递增,所以h(x)min=h(1)=4.所以a≤h(x)min=4.故a的取值范围是(∞-,4].答案B9.(·青岛一模)已知函数f(x)=x3+bx2+cx的图象如图所示,则x+x等于()A.B.C.D.解析由题图可知f(1)=0,f(2)=0,∴解得∴f(x)=x3-3x2+2x,∴f′(x)=3x2-6x+2.由图可知x1,x2为f(x)的极值点,∴x1+x2=2,x1x2=.∴x+x=(x1+x2)2-2x1x2=4-=.答案C10.(·湖北卷)已知函数f(x)=x(lnx-ax)有两个极值点,则实数a的取值范围是()A.(∞-,0)B.C.(0,1)D.(0∞,+)解析由题知,x>0,f′(x)=lnx+1-2ax,由于函数f(x)有两个极值点,则f′(x)=0有两个不等的正根,即函数y=lnx+1与y=2ax的图象有两个不同的交点(x>0),则a>0;设函数y=lnx+1上任一点(x0,1+lnx0)处的切线为l,则kl=y′=,当l过坐标原点时,=⇒x0=1,令2a=1⇒a=,结合图象知0