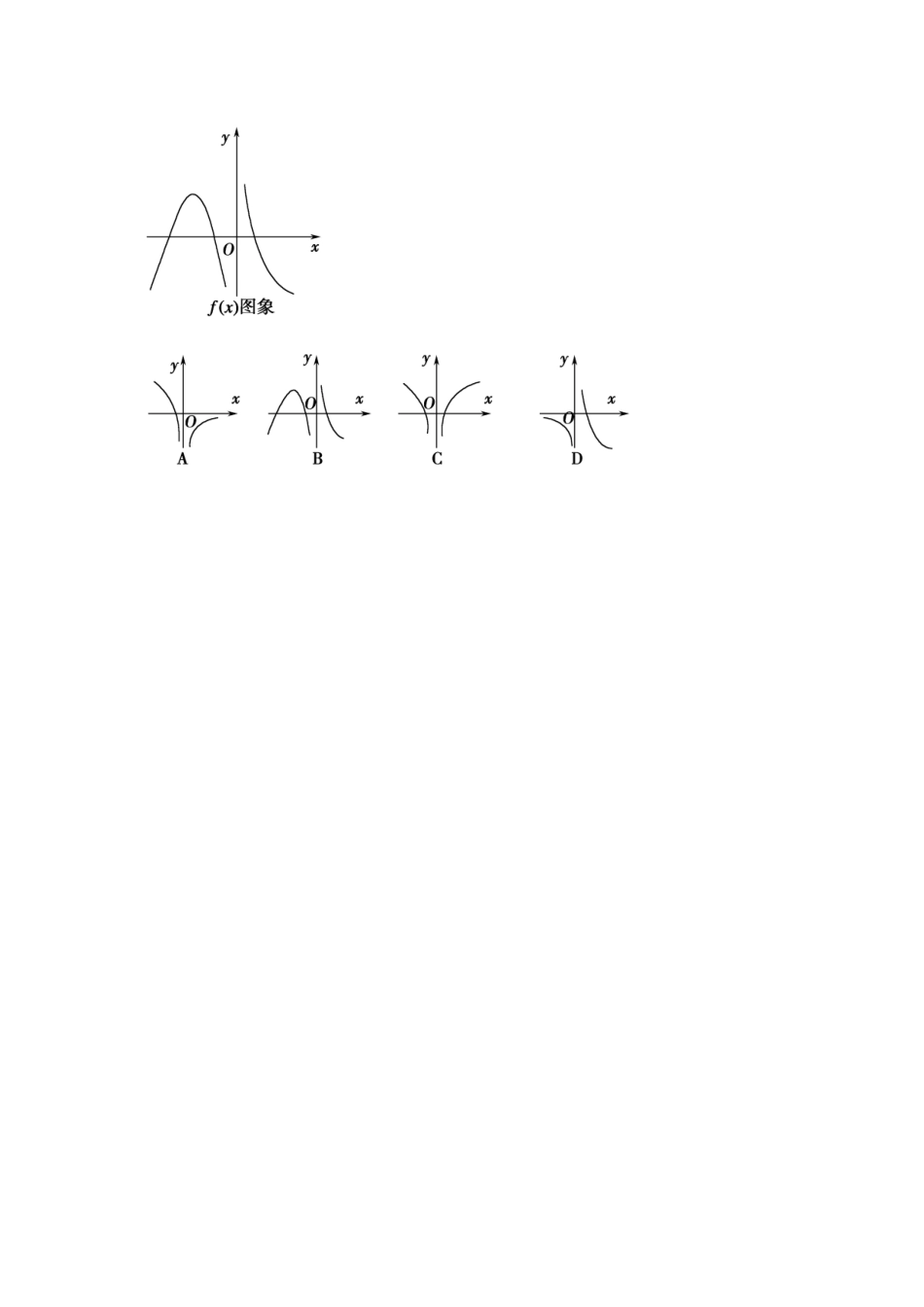
阶段回扣练3导数及其应用(建议用时:90分钟)一、选择题1.已知曲线y=-3lnx的一条切线的斜率为,则切点的横坐标为()A.3B.2C.1D.解析由题意y′=-,设切点P(x0,y0),x0>0,则-=,解得x0=3或x0=-2(舍),故选A.答案A2.(·大连模拟)曲线y=x2+lnx在点(1,1)处的切线方程为()A.3x-y-2=0B.x-3y+2=0C.3x+y-4=0D.x+3y-4=0解析y′=2x+,故y′|x=1=3,故在点(1,1)处的切线方程为y-1=3(x-1),化简整理得3x-y-2=0.答案A3.若函数f(x)=在x=1处取极值,则a=()A.1B.2C.3D.4解析f′(x)=′==, x=1为函数的极值点,∴f′(1)=0,即1+2×1-a=0,解得a=3,故选C.答案C4.函数f(x)=-,a<b<1,则()A.f(a)=f(b)B.f(a)<f(b)C.f(a)>f(b)D.f(a),f(b)大小关系不能确定解析f(x)=-,所以f′(x)=-=,当x<1时,f′(x)<0,所以函数f(x)=-在(∞-,1)上是减函数,又a<b<1,故f(a)>f(b).答案C5.函数f(x)=mx3-x在(∞-,∞+)上是减函数,则m的取值范围是()A.(∞-,0)B.(∞-,1)C.(∞-,0]D.(∞-,1]解析由题意知,f′(x)=3mx2-1≤0在(∞-,∞+)上恒成立,x①=0时,-1≤0恒成立,即m∈R;x≠0②时,有m≤在R上恒成立, >0,∴m≤0,综上m≤0,故选C.答案C6.设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则函数y=f′(x)的图象可能是()解析如图所示,当x∈(∞-,x0)时,函数f(x)为增函数,当x∈(x0,0)和x∈(0,∞+)时,函数f(x)为减函数,∴x=x0是函数f(x)的极大值点,可得f′(x0)=0,且当x∈(-∞,x0)时,f′(x)>0,当x∈(x0,0)和x∈(0,∞+)时,f′(x)<0.由此对照各个选项,可得函数y=f′(x)的图象只有A项符合.答案A7.用总长14.8m的钢条制作一个长方体容器的框架,若容器底面的长比宽多0.5m,要使它的容积最大,则容器底面的宽为()A.0.5mB.0.7mC.1mD.1.5m解析设容器底面的宽为xm,则长为(x+0.5)m,高为(3.2-2x)m.由3.2-2x>0和x>0,得0<x<1.6.设容器的容积为ym3,则有y=x(x+0.5)(3.2-2x),其中0<x<1.6,整理得y=-2x3+2.2x2+1.6x,所以y′=-6x2+4.4x+1.6.令y′=0,得x=1.从而在定义域(0,1.6)内只有当x=1时y取得最大值,即容器底面的宽为1m时,容器的容积最大.答案C8.(·青岛一模)已知函数f(x)=x3+bx2+cx的图象如图所示,则x+x等于()A.B.C.D.解析由题图可知f(1)=0,f(2)=0,∴解得f∴(x)=x3-3x2+2x,∴f′(x)=3x2-6x+2.由图可知x1,x2为f(x)的极值点,x1∴+x2=2,x1x2=.x∴+x=(x1+x2)2-2x1x2=4-=.答案C9.函数f(x)的定义域是R,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式ex·f(x)>ex+1的解集为()A.{x|x>0}B.{x|x<0}C.{x|x<-1或x>1}D.{x|x<-1或0<x<1}解析构造函数g(x)=ex·f(x)-ex.因为g′(x)=ex·f(x)+ex·f′(x)-ex=ex[f(x)+f′(x)]-ex>ex-ex=0,所以g(x)=ex·f(x)-ex为R上的增函数.因为g(0)=e0·f(0)-e0=1,所以原不等式转化为g(x)>g(0),解得x>0.答案A10.(·河北模拟)若不等式2xlnx≥-x2+ax-3对x∈(0,∞+)恒成立,则实数a的取值范围是()A.(∞-,0)B.(∞-,4]C.(0,∞+)D.[4,∞+)解析2xlnx≥-x2+ax-3,则a≤2lnx+x+,设h(x)=2lnx+x+(x>0),则h′(x)=.当x∈(0,1)时,h′(x)<0,函数h(x)单调递减;当x∈(1,∞+)时,h′(x)>0,函数h(x)单调递增,所以h(x)min=h(1)=4.所以a≤h(x)min=4.故a的取值范围是(∞-,4].答案B二、填空题11.已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(e)+lnx,则f′(e)=________.解析f′(x)=2f′(e)+,取x=e,得f′(e)=2f′(e)+,由此解得f′(e)=-=-e-1.答案-e-112.已知2≤(kx+1)dx≤4,则实数k的取值范围是________.2≤k∴+1≤4≤,∴k≤2.答案13.设f(x)=lnx-a,若f(x)<x2在x∈(1,∞+)上恒成立,则实数a的范围为________.解析 函数f(x)=lnx-a,且f(x)<x2在(1,∞+)上恒成立,∴函数f(x)=lnx-a<x2在(1,∞+)上恒成立,∴a>lnx-x2.令h(x)=lnx-x2,有h′(x)=-2x. x>1,∴-2x<0...